Prerpints.org logo
Preprint
Article

Robustness of Single and Dual-Energy Deep Learning-Based Scatter Correction Models on Simulated and Real Chest X-rays

Altmetrics

Downloads

71

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 November 2023

Posted:

16 November 2023

You are already at the latest version

Alerts
Abstract
Chest X-ray (CXR) is the first tool globally employed to detect cardiopulmonary pathologies. These acquisitions are highly affected by scattered photons due to the large field-of-view required. Scatter in CXRs introduces background in the images, which reduces their contrast. We developed three deep learning-based models to estimate and correct the scatter contribution to CXRs. We used a Monte Carlo (MC) ray-tracing model to simulate CXRs from human models obtained from CT scans using different configurations (depending on the availability of dual-energy acquisitions). The simulated CXRs contained the separated contribution of direct and scattered X-rays in the detector. These simulated datasets were then used as the reference for the supervised training of several NN. Three NN models (single and dual energy) were trained with the MultiResUNet architecture. The performance of the NN models was evaluated on CXRs obtained with the MC code from chest CTs of patients affected by COVID-19. The results showed that the NN models were able to estimate and correct the scatter contribution to CXRs with an error <5%, being robust to variations in the simulation setup and improving the contrast in soft tissue. The single-energy model was tested with real CXRs, providing robust estimations of the scatter-corrected CXRs.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Chest X-ray radiography (CXR) is usually the first imaging technique employed to perform an early diagnosis of cardiopulmonary diseases. Typical pathologies detected in CXRs include pneumonia, atelectasis, consolidation, pneumothorax or pleural and pericardial effusion [1]. Since the COVID-19 pandemic started in 2020, it is also used as a tool to detect and assess the evolution of the pneumonia caused by this condition [2]. CXR is used worldwide thanks to the simplicity with which it can be completed, the low cost, low radiation dose, and its sensitivity [3,4].
Regarding the position and orientation of the patient in relation to the X-ray source, the desired and most frequently used setup is the posteroanterior (PA) projection [5], since it provides better visualization of lungs [6]. However, this configuration requires the patient to be standing erect, which is not possible for critically ill patients, intubated patients or some elderly people [6,7]. In these situations, it is more convenient to carry out the anteroposterior (AP) projection, in which the patient can be sitting up in bed or lying in supine position. Thus, AP image can be acquired with a portable X-ray unit outside the radiology department too, when the patient’s condition advises not to shift him/her [6].
X-ray imaging is based on the attenuation that photons suffer when they traverse the human body, so that photons that cross the body and reach the detector without interacting with the media, i.e. primary photons, form the image [8]. However, there are also photons that interact with the media and are not absorbed, but they are scattered. This secondary radiation can also get to the detector, representing background noise and causing blurring in the primary image and a considerable loss in contrast-to-noise ratio (CNR) [9]. This effect is especially relevant in CXR due to the requirement of large detectors (at least 35 cm side) to be able to cover the whole region of interest (ROI) [10]. To overcome this problem, several techniques have been proposed, which can be split into two types: scatter suppression and scatter estimation [11]. Scatter suppression methods aim to remove, or at least reduce, the scattered photons that arrive at the detector, while scatter estimation methods try to obtain the signal just of the secondary photons, and then subtract it from the total projection.
The most widely used scatter correction method is the anti-scatter grid, where a grid is interposed between the patient and the detector in a way that scattered photons are absorbed while primary photons are allowed to pass [7,12]. This technique is successfully implemented in clinical practice [10] since many clinical systems incorporate this grid [13], although it has some disadvantages. Firstly, an anti-scatter grid can also attenuate primary radiation leading to noisy images [9,10]. Besides, it can generate grid line artifacts in the image [14] and it can increase the radiation exposure between two and five times [5,15]. Finally, in AP acquisitions it is difficult to accurately align the grid with respect to the beam, so the use of anti-scatter grid in combination with portable X-ray units used at intensive care units or with patients that cannot stand up is more time-consuming and does not guarantee a good result [7,13]. Another method studied to physically remove the scattered X-rays consists in increasing the air gap between the patient and the detector, which enlarges the probability that secondary photons miss the detector due to large scatter angles [16,17]. This approach causes a smaller increase in the radiation dose than the anti-scatter grid, but it can magnify the acquired image [5]. Other alternatives to the use of the anti-scatter grid are the slit scanning, with the drawback of an increase of acquisition times, or a strict collimation, which compromises the adaptability of the imaging equipment [10,11,13].
Regarding scatter estimation, there are some experimental methods such as the beam stop array (BSA), which acquires a projection of just the scatter radiation (primary photons are removed) and then it is subtracted from the standard projection [18]. However, most techniques to estimate the scatter radiation are software-based [19,20,21]. In this field, Monte Carlo (MC) simulations are gold-standard. MC codes reproduce in a realistic and very accurate way the interactions of photons (photoelectric absorption and Rayleigh and Compton scattering) in their path through the human body. Therefore, these models are able to provide precise estimations of scatter [9,13,19]. The major drawback of MC simulations is the high computational time they require, which makes it difficult to implement in real-time clinical practice [9,19]. Model-based methods make use of simpler physical models, so they are faster than MC at the cost of much less accuracy [13]. Similarly, kernel-based models approximate the scatter signal by an integral transform of a scatter source term multiplied by a scatter propagation kernel [11,21]. Nevertheless, this method depends on each acquisition setup (geometry, image object or X-ray beam spectrum), so it is not easy to generalize [19].
Recently, deep learning algorithms have been widely used for several medical imaging analysis tasks, like object localization [22,23], object classification [24,25] or image segmentation [26,27]. Particularly, convolutional neural networks (CNN) have succeeded in image processing, outperforming traditional and state of the art techniques [3,26,28]. Among them, the U-Net, first proposed by Ronneberger et al in 2015 [26] for biomedical image purposes, and its subsequent variants such as the MultiResUNet are the most popular networks [28]. In particular, there are some works that make use of CNN to estimate scatter either in CXR or computed tomography (CT). In Maier et al [19], they used a U-Net like deep CNN to estimate the scatter in CT images, training the network with MC simulations. In a similar way, Lee & Lee [9] used MC simulations to train a CNN for image restoration, that is, the scatter image is estimated, and then it is subtracted from the CNN input image (the scattered image), obtaining as output the scatter-corrected image. In that case, they applied the CNN to CXRs, which are then used to reconstruct the corresponding cone-beam CT image. Roser et al [13] also used a U-Net in combination with prior knowledge of the X-ray scattering, which is approximated by bivariate B-splines, so that spline coefficients help to calculate the scatter image for head and thorax datasets.
Dual-energy X-ray imaging was first proposed by Alvarez and Macovski in 1976 [29]. This technique takes advantage of the dependence of the attenuation coefficient with the energy of the photon beam and the material properties, i.e. its mass density and atomic number. In dual-energy X-ray, two projections using two different energy spectra in the range of 20-200 kV are acquired. They can provide extra information with respect to a common single-energy radiography, allowing to better distinguish different materials [30,31,32]. In this way, dual-energy X-ray imaging may improve the diagnosis of oncological, vascular or osseous pathologies [30,33]. Specifically, in CXR dual acquisitions are utilized to perform dual energy subtraction (DES), generating two separate images: one of the soft tissue and one of the bone. Soft tissue selective images, in which ribs and clavicle shadows are removed, have been proven to enhance the detection of nodules and pulmonary diseases [34,35].
Several studies have made use of dual-energy X-ray absorption images along with deep-learning methods to enhance medical image analysis. Some examples include image segmentation of bones to diagnose and quantify osteoporosis [36], or estimation of phase contrast signal from X-ray images acquired with two energy spectra [37]. Regarding chest X-rays, the combination of dual energy and deep learning has been used to obtain two separated images with bone and soft tissue components [38]. However, to the best of our knowledge, the application of dual-energy images to obtain the scatter signal has not been yet examined.
In this work, we present a study of robustness of three U-Net-like CNN that estimate and correct the scatter contribution using either single-energy CXRs or dual-energy CXRs to perform the network training. All images were simulated with a Monte Carlo code from actual CTs of patients affected with COVID-19. The scatter-corrected CXRs were obtained by subtracting the estimation of the scatter contribution from the image affected by the scattered rays, which we call uncorrected scatter image. Two different analysis were performed to evaluate the robustness of the models. First, several metrics were calculated to assess the accuracy of the scatter correction, taking the MC simulations as the ground truth, after the algorithms were applied to images simulated with various source-to-detector distances (SDD), including the original SDD with which the training images were simulated. The accuracy of the models with CXRs acquired with the original SDD was taken as reference, and it was compared with the values obtained for the other distances. Secondly, the contrast between the area of the lesion (COVID-19) and the healthy area of the lung was evaluated on soft tissue Dual-Energy Subtraction (DES) images to quantify how scatter removal helps to better identify the affected region. Then, values of contrast in the ground truth were compared with the ones obtained in the estimated scatter-corrected images, just with the original SDD. Finally, the single-energy neural network was tested with a cohort of varied real CXRs, and the ratio between the values of two regions in the lung (with and without ribs) was calculated to determine how the contrast of the image improves after applying the scatter correction method.

2. Materials and Methods

2.1. COVID-19 CT images database

100 chest CTs of COVID-19 patients were taken from the database COVID-19 Lung CT Lesion Segmentation Challenge – 2020 [39], proposed by MICCAI 2020, to carry out the deep-learning training. The database included a mask indicating the affected region for each patient. CTs had 512 pixels in X (lateral) and Z (anteroposterior) direction, while the number of pixels in Y direction (craneo-caudal direction) varied from one patient to another. Pixel size was set equal in the three directions for each patient, but it changed for different patients. The smallest pixel size was 0.46 mm, and its maximum size was 1.05 mm, which left a field-of-view ranging from 236 mm to 538 mm in X and Z directions.

2.2. Monte Carlo simulations to generate training and validation dataset

CTs were represented in Hounsfield Units (HU). These values were converted to mass density following Schneider et al [40]. Besides, the stretcher was removed by setting its HU values as those of the air. CXR projections were acquired from these CTs using an in-house developed, GPU-accelerated, ultrafast MC code [41]. The code provided three projections for each patient: the scatter-free image (only primary photons), the scatter image (only scattered photons, considering both Rayleigh and Compton interactions) and the uncorrected-scatter image (both primary and secondary photon contributions). In all cases, the projections represented the photon energy that reaches the detector when there is an object (i.e. the patient) divided by the photon energy that would reach the detector in a simulation on air (see Figure 1). This way, all projections had values between 0 and 1. To be able to perform dual-energy training, images were acquired with two different X-ray energy spectra corresponding to 60 kVp (low energy) and 130 kVp (high energy) for each case (Figure 2). The parameters of the simulation setup are gathered in Table 1. A total number of 5 · 10 9 photons were simulated to obtain the three projections in the following way: the code tracked photons path; if it had suffered any scatter interaction, its energy when arriving to the detector was used to form the scatter image, and if it had not undergone any interaction the energy was saved to form the scatter-free image. After all photons histories were simulated, the uncorrected-scatter image was calculated as the sum of the scatter and scatter-free projections. Finally, a Gaussian filter was applied to the three images to smooth them. The simulation of the three projections for each energy spectra took about 10 min on a GeForce RTX 2080 Ti GPU.

2.3. CNN Architecture

An enhanced U-Net like architecture named MultiResUNet was used to train the NN models of scatter estimation. This evolution of the classical U-Net was first introduced by Ibtehaz and Rahman in 2019 [28]. It is based on an encoder-decoder model, which in the standard U-Net architecture takes the input image and performs four series of two 3 × 3 convolution operations followed by a 2 × 2 max pooling (encoder part), being the size of the input image downsampled by a factor of 2 in each series. Then, another sequence of two 3 × 3 convolutions joins the encoder and the decoder. The decoder first carries out a 2 × 2 transposed convolution upsampling by a factor of 2 the feature map, which is followed again by a series of two 3 × 3 convolution operations. Finally, a 1 × 1 convolution generates the output image [26]. Furthermore, U-Net architecture adds skip connections between encoder and decoder doing a concatenation between the output of the two convolution operations in the encoder and the output of the upsampling convolution in the decoder. These connections enable the NN to recover spatial data lost due to pooling procedures.
The MultiResUNet presents two main differences with respect to the standard U-Net. First, it substitutes the two consecutive 3 × 3 convolution operations for three different 3 × 3 convolutions, where the 2nd and the 3rd are intended to be approximately as one 5 × 5 and one 7 × 7 procedure, respectively. Then, they are concatenated and a 1 × 1 convolutional layer (residual connection) is added. The result forms the so-called MultiRes block. Additionally, the NN does a batch normalization [44] to every convolutional layer. The second variation is related to the shortcut connections between encoder and decoder. A so-called residual path is computed with 3 × 3 convolutions added to 1 × 1 convolutional filters for residual connections. Then, the result is concatenated with the output of the transposed convolution in the decoder stage [28]. The scheme of the network is presented in Figure 3.
In this work, we used the MultiResUNet architecture with ReLU (Rectified Linear Unit) [45] as activation function in every convolution output, including the last one, which provides the final output of the NN. The initial number of filters was set to 64, which was increased by a factor of 2 in the downsampling steps, and afterward it decreased the same factor in the upsampling processes. In the single-energy model, there was one input and one output channel: the network took pairs of input-output images, being the input image the uncorrected scatter image and the output the fraction of the scatter image with respect to the uncorrected scatter image (scatter ratio), both high energy CXRs acquired with the 130 kVp energy spectrum. In the dual-energy workflow, we tested two different algorithms. On the one hand, a neural network with two input channels, corresponding to the uncorrected scatter projections of low and high energy, and one output channel, representing the same as in the single-energy model (scatter ratio for the high energy case). From now on, we will refer to this model as 1-output dual-energy model. On the other hand, we developed a 2-output dual-energy model, which had two input and two output channels, that is to say, it is able to estimate at the same time the scatter ratio of the low and high energy images. The single-energy model and the 1-output dual-energy model were also trained with the low energy images in order to obtain the corresponding scatter-corrected estimations. Figure 4 shows a scheme of the input and output images corresponding to each of the described models. The introduction of the scatter ratio as the output of the NN ensures that the image has values in the range 0 – 1, which is the standard range used for the training of neural networks and allows the use of the ReLU as activation function in the output layer.
The MultiResUNet was trained on Google Colab platform [46,47] on a Tesla T4 GPU, with 600 epochs using an Adam optimizer (with default parameters) [48], 10 steps per epoch, batch size of 24, and the mean squared error (MSE) as loss function. The original size of input and output images was equal to the resolution of the detector, i.e. 2050 × 2050 . To avoid memory problems, images were downsized to 128 × 128 using bilinear interpolation. Besides, images were cropped in the craneo-caudal direction to remove the edges (air voxels). After this action, the image size was 96 × 128 . We split the dataset into 70 training cases and 30 validation cases. As this number of cases is not enough to properly train a convolutional neural network, we performed data augmentation, including vertical and horizontal flips and zoom in up to 50%. These operations still provided realistic images.
The output of the network is multiplied by the uncorrected scatter image, obtaining the scatter estimation. Then, the scatter estimation is subtracted from the input image, getting the estimated scatter-corrected image. The software takes 1.5 s to provide the scatter correction for each case, and multiple cases could be estimated simultaneously.

2.4. Evaluation of scatter estimation models on simulated CXRs

To assess the performance of the trained models, an additional test set of 22 CT images was taken from the same COVID-19 Lung CT Lesion database, and the three projections (scatter, scatter free and uncorrected scatter) were simulated as explained in Section 2.2. Four metrics were evaluated to quantify the accuracy of the scatter correction with the single and dual-energy NN models for the test set: the mean squared error (MSE), the mean absolute percentage error (MAPE), the structural similarity index (SSIM) and the relative error ( E r e l ), which are defined as: This is the example 1 of equation:
M S E = 1 M · N ∑ i = 1 M ∑ j = 1 N ∥ x i , j − y i , j ∥ 2
M A P E = 1 M · N ∑ i = 1 M ∑ j = 1 N | x i , j − y i , j | | x i , j | · 100
S S I M = 1 M · ∑ i = 1 M ∑ j = 1 N 2 μ x μ y + c 1 2 σ x y + c 2 μ x 2 + μ y 2 + c 1 σ x 2 + σ y 2 + c 2 · 100
E r e l = 1 M · N ∑ i = 1 M ∑ j = 1 N | x i , j − y i , j | x i , j + y i , j
where M and N are the number of pixels in X and Y direction, and x i , j and y i , j are the values of the ground truth and the estimated images, respectively, for pixel ( i , j ) . In Equation 3, μ x and μ y are the average of x i , j and y i , j ; σ x and σ y are the standard deviations of x i , j and y i , j ; σ x y is the covariance of x i , j and y i , j ; c 1 = ( K 1 L ) 2 and c 2 = ( K 2 L ) 2 , where L represents the range of pixel values and K 1 and K 2 are small positive constants that keep the denominator non-zero [49,50]. Metrics were applied to a region of interest (ROI) focused on the lungs.
The 22 CT test cases were simulated with 10 additional source-to-detector distances different from the one used to train the NN algorithms (SDD=180 cm, see Table 1), from 100 to 200 cm. Then, the robustness of the models to variations in the SDD was evaluated with the metrics above-mentioned (Equations 1–4).
To determine the gain when correcting the scatter, a comparison of the contrast value between the COVID-19 affected region in the lung and the non-affected region on soft tissue images was performed. Soft tissue images were calculated performing dual energy subtraction, that is, subtracting the low energy CXR from the high energy CXR. This operation was carried out for the uncorrected scatter CXRs, the ground truth scatter-corrected CXRs (Figure 5), and the estimated scatter-corrected CXRs with the three NNs. A mask of the COVID-19 region for each CT was found in the original database, so the COVID-19 region corresponding to the 2D projection was obtained with the MC simulation (Figure 6a). The lung mask was calculated with a U-Net CNN previously trained, with batch normalization, Adam optimizer, the binary cross entropy as loss function and sigmoid as output activation; and the mask of the healthy lung region was obtained by subtracting the COVID-19 mask from the lung mask (Figure 6b).
The contrast metric is calculated as follows:
C = 1 F ∑ k = 1 F i m g k 1 G ∑ l = 1 G i m g l
where F and G stand for the total number of pixels in the COVID-19 and the healthy-lung mask, respectively, and i m g ( k ) and i m g ( l ) represent the values of the given image i m g in pixel k (COVID mask) or in pixel l (healthy-lung mask). To evaluate the contrast, each lung was considered as a different case for patients who have both lungs affected, so there are 31 affected lungs in which the contrast was calculated. The accuracy of the NN models regarding the contrast was quantified by the relative difference with respect to the ground truth value:
D i f r e l = 100 · | C g t − C N N | C g t
where C g t is the contrast value in Equation 5 for the scatter-free ground truth image (from MC simulation), and C N N is the contrast value for the NN estimation (single or dual-energy model) of the scatter correction.
Additionally, the percentage contrast improvement factor (PCIF) was computed in the following way:
P C I F = 100 · C c o r r C u n c o r r − 1
where C c o r r and C u n c o r r are the contrast values for the scatter corrected and uncorrected image, respectively, calculated from Equation 5.

2.5. Evaluation of scatter correction on true CXRs

A set of 10 real CXRs acquired without the anti-scatter grid were taken from the MIMIC-CXR database [51,52] to test the single-energy model for high energy CXRs on true data. To introduce these images as the input of the neural network, some operations must be performed. Firstly, the CXR in Dicom format is loaded in a Python environment as a numpy array. Then, the edges of the images that do not contain information are cropped, so that they are focused on the lungs region in a way that they look like the training and validation images. The original size of the CXRs selected from the database is 2544 × 3056 , so they are rescaled to 96 × 128 , as it was done before with the simulated images (see Section 2.3). Finally, the values of the pixels in the true images must be converted to the same scale as in the training, simulated images. The values of the real CXR represent the logarithm of the initial beam intensity ( I 0 ) divided by the intensity that arrives at the detector (I), while the values depicted in the training images are I / I 0 , as explained in Section 2.2. So the transformation of the pixel values is done following the Beer-Lambert law [53]: I = I 0 · e − μ · x , where μ is the linear attenuation coefficient of the material and x is the path length of the beam through the material; and then adjusting the scale so that the minimum and maximum values corresponding to bone and lungs are similar as in the simulated images, as well as the ratio between them.
The output of the CNN, i.e., the scatter fraction, is multiplied by the downsized and scale-transformed CXR, yielding the estimation of the scatter contribution in low resolution. To obtain the final scatter-corrected CXR, the native resolution is recovered in the image of scatter by means of bilinear interpolation. Then, the high-resolution scatter image is subtracted from the high-resolution, scale-transformed CXR, giving the high-resolution scatter-corrected image.
The performance of the single-energy model on real data is quantitatively evaluated by means of the ratio between a region of the lung with and without ribs on it:
R a t i o = 1 L ∑ m = 1 L i m g m 1 R ∑ n = 1 R i m g n
where L and R stand for the total number of pixels of the lung rib-free region and lung rib region, respectively, and i m g ( m ) and i m g ( n ) represent the values of the given image i m g in pixel m (rib-free region) or in pixel n (lung rib region). The comparison of the ratio obtained in the original CXR (affected by the scatter) and in the estimation of the scatter-corrected image determine if the NN algorithm provides images with a better contrast between different tissues.

3. Results

3.1. Accuracy of scatter correction on simulated CXRs

An example of the high energy, scatter-corrected ground truth image, and the scatter-corrected estimations of the single-energy model and the 1-output and 2-output dual-energy models are represented in Figure 7 for one of the test cases with SDD=180 cm.
The values of MSE, MAPE, SSIM and the relative error for the test cases with the original SDD and the ten additional variations are represented with a box plot (Figure 8). The results of the four metrics show that the scatter correction models provide an accurate estimation of the scatter correction for the original source-to-detector distance (SDD=180 cm), highlighted with red box. For the high energy images, the average MSE is in the order of 7.3 · 10 − 6 , the MAPE indicates an average precision of 11.2%, 8.6% and 7.6%, while the relative error presents mean values of 4.8%, 4.0% and 3.6% for the single, 1-output dual-energy and 2-output dual-energy models, respectively. Besides, the average SSIM is 0.997 for the single-energy algorithm and 0.998 for both dual-energy NNs, which demonstrates that the outputs of the models have an elevated structural similarity with the ground truth images.
Regarding the scatter correction of low energy images, the average MSE in the single-energy model is 2.2 · 10 − 6 , and 1.5 · 10 − 6 for the two dual-energy networks. The MAPE is 17.1%, 14.0% and 16.6% for the single-energy, 1-output dual-energy and 2-output dual-energy models, respectively, while the relative error has average values of 7.3%, 6.7% and 7.0%. The SSIM obtained in the three models is on average 0.999. Comparing the estimations for the high energy and low energy images, it is observed that the MAPE and the relative error are higher in the models for low energy scatter correction estimations, but a good accuracy is still achieved.
In all graphics in Figure 8, it is observed that the mean values of the metrics evaluated over the test cases keep very similar for the different SDD in relation to the original SDD with which the neural networks were trained. In the high energy estimations, the biggest increase among all the evaluated SDD for the MSE is 22.6% in the single-energy model, 15.5% in the 1-output dual-energy model and 2.4% in the 2-output dual-energy model. In the MAPE, the greatest deviation from the mean value corresponding to SDD=180 cm is 7.3%, 10.7% and 3.9%, respectively. In the SSIM, the differences among the various SDD cases are barely relevant (0.06%, 0.04% and 0.01%), while the major differences in the relative error are in the same order that the ones in the MAPE (7.6%, 8.6% and 2.5% for single, 1-output and 2-output dual-energy algorithms, respectively). For its part, in the low energy estimations similar results are obtained: the major deviations are 3.1%, 14.0% and 6.3% in MSE; 8.2%, 5.7% and 9.0% in MAPE; and 4.1%, 4.5% and 5.7%, for the single-energy, 1-output and 2-output dual-energy models. Again, the variations in SSIM are negligible. In all cases, the biggest deviations with respect to the original SDD are found either in SDD=100 cm or SDD=200 cm. Furthermore, graphics in Figure 8 show that the range of the maximum and minimum values of the metrics for the 22 test cases keeps as well much the same in all SDDs in comparison with the original one.
Comparing the results of single and dual-energy models, Figure 8 shows that the 2-output dual-energy algorithm yields higher accuracy in scatter correction considering the metrics of MAPE, SSIM and relative error for the high energy CXRs, while in the low energy images the best accuracy is obtained with the 1-output dual-energy algorithm. Taking as reference the case of SDD=180 cm, in the high energy estimations the average value of MAPE yielded by the 2-output dual-energy NN is a 13% smaller than the one of the 1-output dual-energy model, and a 47% smaller with respect to the single-energy algorithm; the relative error is a 33% and an 11% better, respectively, while the SSIM is just a 0.15% bigger in the 2-output dual-energy model than in the single-energy model, and 0.04% bigger with respect to the 1-output dual-energy NN, although a visual difference can be appreciated in the corresponding graphics. In the low energy case, the 1-output dual-energy model outperforms the single-energy and the 2-output dual-energy algorithms in a 22% and 19% in MAPE, and a 9% and 4% in the relative error, respectively. The difference in the SSIM is minimal. Besides, it is observed in Figure 8 that the model with the best accuracy in each case also has a lower standard deviation, represented by a smaller size of the box in the plot (green boxes in the metrics for low energy estimations, corresponding to the 1-output dual-energy model, and violet boxes in the high energy estimations, corresponding to the 2-output dual-energy model. The relevance of the differences between the three algorithms will be further discussed in Section 4.

3.2. Study of contrast improvement after scatter correction

Table A1 in the Appendix shows the contrast between the region affected by COVID-19 and the healthy lung area in the soft tissue DES images. In 24 out of the 31 cases, the scatter-corrected ground truth DES has a higher contrast than the uncorrected DES, meaning that the scatter correction will help to better identify the lesion. In these cases, the average contrast improvement in the area of the lesion is 9.5%, having a maximum value of 20.7% (see Figure 9a).
It can be observed in Figure 9a that the three scatter correction methods proposed in this work are able to provide a very accurate percentage contrast improvement factor, if results are compared with the ground truth (taken from the MC simulation). The single-energy model yields an average contrast improvement of 7.7%, being the maximum 17.4%, while the 1-output dual-energy model gives an average PCIF of 8.6% and a maximum of 18.7%, and in the 2-output dual-energy NN the average PCIF is 9.4% and its maximum value is 20.5%. These numbers indicate again that the 2-output dual-energy model has the best performance, although the difference with the other two algorithms is small and the three models are acceptable. Figure 9b represents the relative difference between the ground truth contrast value and the contrast value estimated by the three NN models, and it reinforces what was explained for Figure 9a: the relative difference is smaller for the 2-output dual-energy model, being in the range of 0 - 4.4%, with a mean value of 1.0%. For its part, the relative difference for the single-energy results varies from 0.2% to 4.7%, and the average relative difference is 1.8%; while for the 1-output dual-energy model the relative difference is between 0.2% and 4.1%, being on a average 1.3%. All these results point out that the contrast improvement factor associated with the scatter correction is estimated with a very high precision by the three deep learning-based models.

3.3. Study of scatter correction on true CXRs

Figure 10 shows the estimations of the scatter contribution and the scatter-corrected images of three of the real CXRs after applying the single-energy algorithm, along with the corresponding image used as input of the network, that is the original CXR (with scatter) with pixel values transform as explained in Section 2.5. In all cases, the NN model is able to make a proper estimation of the scattered-rays image, and thus provide a scatter-corrected image comparable to what it was expected according to the ground truth simulation and the corresponding estimations (see Figure 1 and Figure 7), both qualitative and quantitatively.
Table 2 shows the ratio between a region of the lung with and without rib in the CXR before and after the single-energy, scatter correction algorithm is applied to the 10 test images. The ratio increases in every sample when the NN model of scatter correction is implemented, being the average rise a 15.0% for the selected cohort, with a maximum increase of 40.2%.

4. Discussion

In this work, we have implemented and evaluated the performance of three deep learning models that estimate and correct the scatter in CXRs. One model is based on standard single energy acquisitions, while the other two models assume that two CXRs with different energies (dual energy) were acquired per patient. The impact of varying the distance of the X-ray source on the accuracy of the scatter correction with these methods was studied.
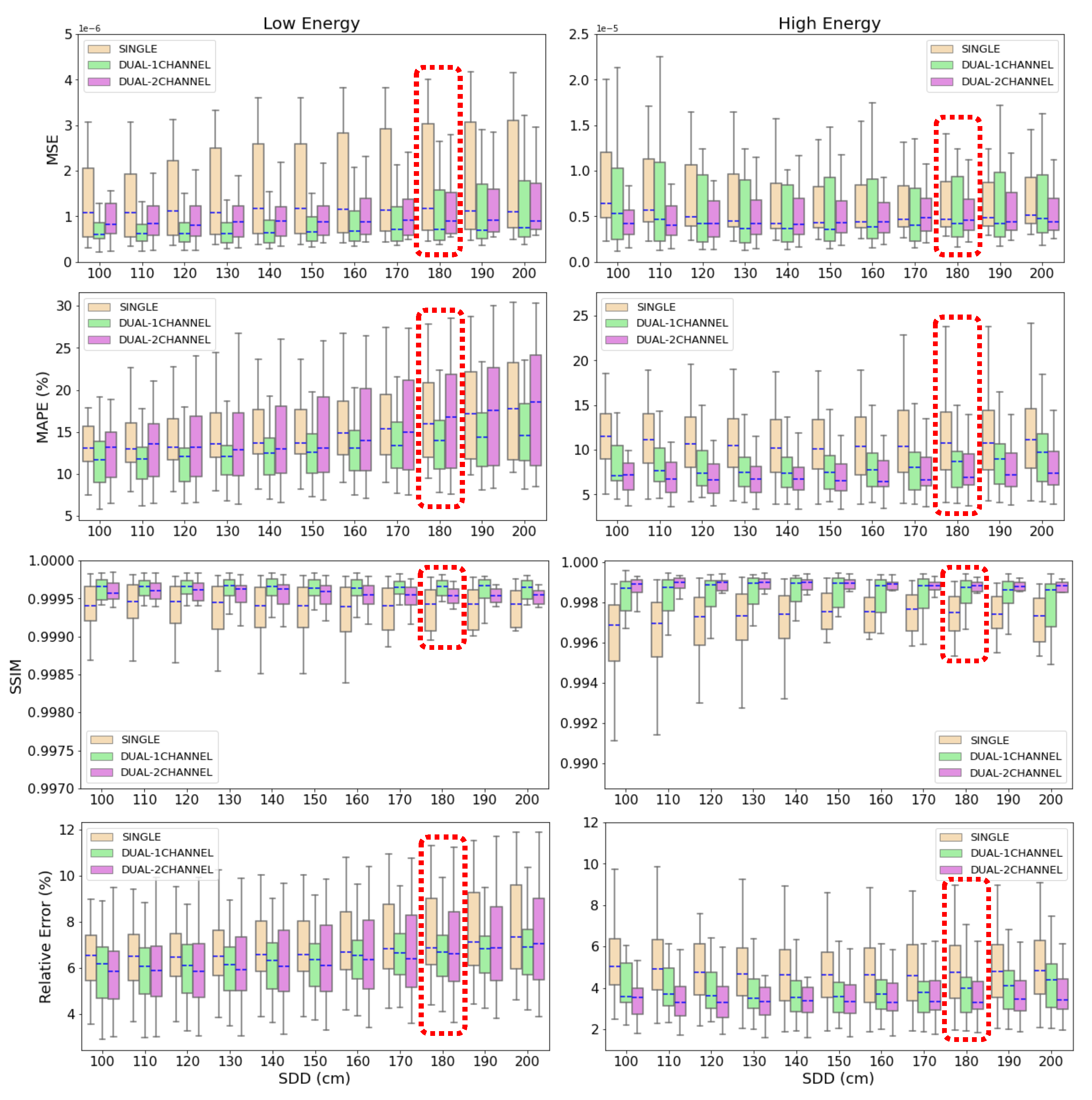
Results in Figure 8 demonstrate that the three deep learning-based models are able to accurately estimate and correct scatter contribution to simulated CXRs. Moreover, the three algorithms keep their accuracy on scatter correction when the source-to-detector distance (SDD) is varied in a range of 100 cm from the SDD used to train the neural networks. Thus, the results prove that the models are robust to variations on the setup parameters like air gap or SDD and their application is not limited to a specific configuration.
The highest decrease in accuracy is found in SDD=100 cm and SDD=200 cm (the neural networks were trained with SDD=180 cm). For SDD=100 cm, this result could be expected since it is the case with the largest distance with respect to the reference SDD. The fact that less accurate metrics are obtained for SDD=200 cm, which is the second closest distance to the one of reference, indicates that the models are more accurate if the images are well focused on the lungs and the air-background areas are reduced or cropped. In this case, lungs get smaller in the image as the SDD increases, which explains the lost in accuracy.
According to the mean values of MAPE and relative error shown in Section 3.1, the results obtained with the dual-energy NN models are more accurate than the ones provided by the single-energy model. In the estimations of the scatter-corrected high energy CXRs, the p-value between the metrics yielded by the 2-output dual-energy and the single-energy models is p = 4.2 · 10 − 13 for the MAPE and p = 0.01 for the relative error. That is, in both metrics the p-value is below the classic threshold of 0.05 [54,55], indicating that the difference is statistically significant. In the low energy estimations, the p-value between the 1-output dual-energy and the single-energy algorithms is p = 0.05 for the MAPE and p = 0.28 for the relative error, so the difference is significant only in the first metric. As it was explained in Section 3.1, the difference in the SSIM is minor. Regarding the MSE, there is not a substantial difference between the three models due to the fact that this is the metric employed as loss function in the training of the algorithms, so it is minimized in both cases. In the comparison between the two proposed models of scatter correction, it is also observed in Figure 8 that there is less deviation in the values of MAPE and relative error applying the dual-energy model. In the high energy case, the standard deviation in MAPE is 4.9%, 3.4% and 2.6% for single-energy, 1-output and 2-output dual-energy models, respectively, and the deviation in the relative error is 1.8% for the single-energy network, 1.4% for the 1-output dual-energy algorithm and 1.1% for the 2-output-dual-energy algorithm. In the low energy case, the standard deviation in MAPE is 6.0%, 4.1% and 6.3% for the single-energy, 1-output and 2-output dual-energy models, and the corresponding values in the relative error are 2.0%, 1.5% and 2.2%, respectively. All these results point out the superior performance of the dual-energy models for scatter correction of CXRs, being more accurate the 1-output model for low energy acquisitions, and the 2-output model for high energy images.
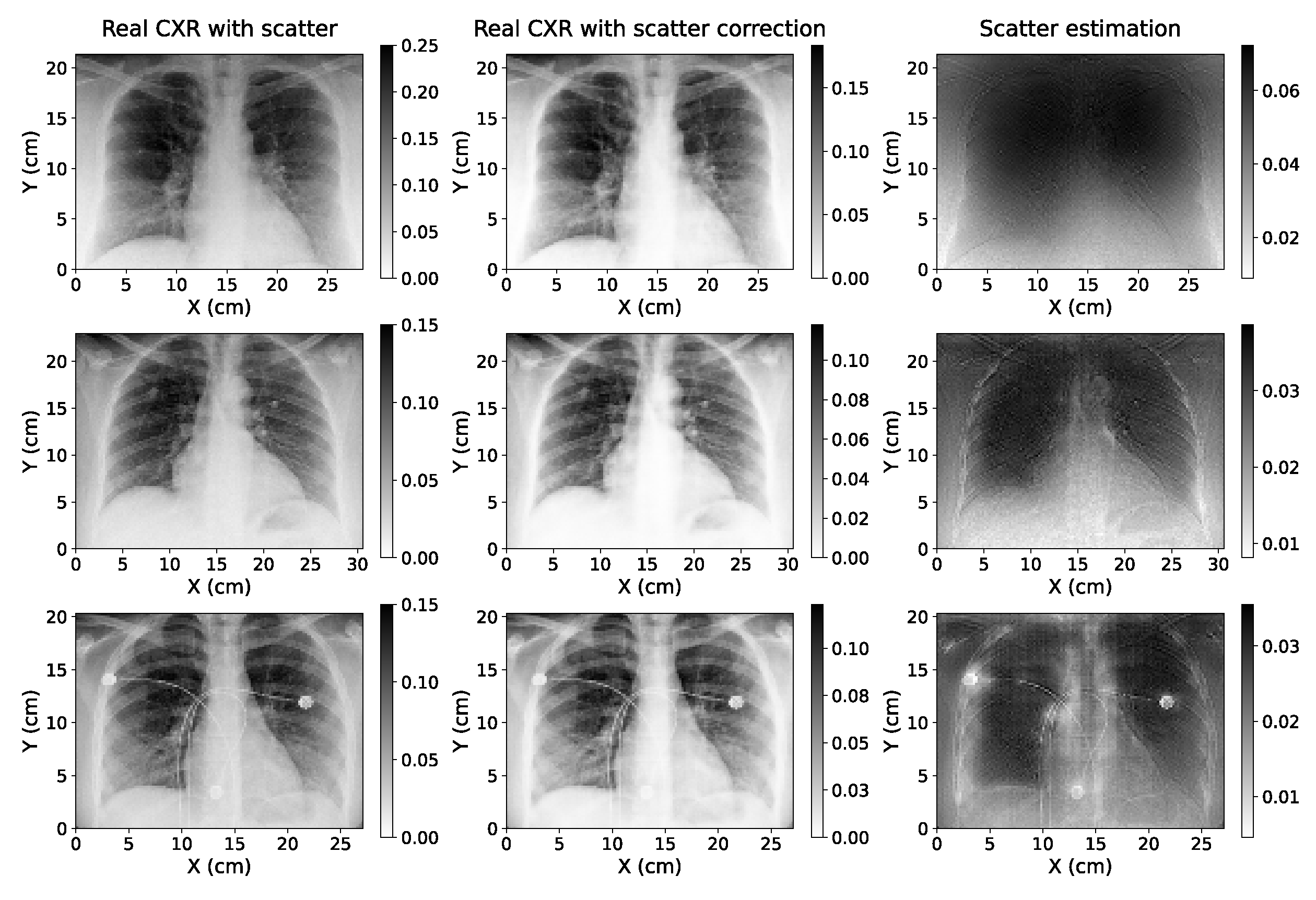
The application of the single-energy model to real CXRs acquired without an anti-scatter grid suggests that the algorithm can be easily adapted to be used with true data acquired with different setups, since in this case the information of the parameters with which the projections were taken was not available in the anonymized Dicom headers used. Furthermore, the accuracy of the model applied to these images could not be quantitatively determined as there was no access to ground truth scatter-free CXRs. However, Figure 10 shows that the estimations are robust, even for a radiography with artifacts such as wires, as it happens in the third case of this figure. This is a key aspect since the application of these models can be specially useful for critically ill patients where it is harder to utilize the anti-scatter grid (as it was explained in Section 1). In addition, the values of the ratio between the regions of the lung with and without ribs (Table 2) point out that the scatter correction improves the contrast between different tissues.
The two dual-energy models could not be verified against real data since we currently do not have access to CXRs acquired with two different X-ray kilovoltages. Nevertheless, it is expected that good estimations of scatter-corrected images can be obtained in actual images, in light of the results shown in Section 3.1 and Section 3.3. Moreover, the superior accuracy shown by the 1-output and 2-output dual-energy models when evaluating the MAPE and the relative error, which has been previously discussed in this section and in Section 3.1, would be worthy to be studied in a future research with real CXRs acquired without the anti-scatter grid with two different energy spectra. This way, it could be determined if dual-energy approaches truly provide better scatter correction, and it also could be tested the gain in DES images after scatter correction.
In the works of Lee & Lee [9], they perform a similar study on CXR scatter correction using CNN and Monte Carlo simulations to generate training cases. They evaluated the SSIM, among other metrics, obtaining an average value of 0.992. This is in the same order of the 0.997 value yielded by the models herein proposed, being our SSIM a 0.5% better. As stated by these authors [9], the application of deep learning to scatter correction of CXR has recently started, so there are not many studies with which results can be compared. Some literature can be found on scatter correction (or estimation) on cone beam CT images. Roser et al. [13] presented a scatter estimation method based on a deep-learning approach helped by bivariate B-spline approximation. For thorax CT, the MAPE ranges from 3% to 20% approximately for the five fold cross-validations, while our models get average values of 11.2% and 8.6%. Additionally, the SSIM for the thorax CT study is between 0.96 and 0.99. Although CT and CXR have some obvious differences and they are not exactly comparable, it can be noticed that our models present a similar precision.
The models displayed in this paper still have some limitations that would need further study. First, we uniquely employed simulated images for the training and validation, as well as for the test cases in Section 3.1. Thus, when these NN are applied to real chest X-ray acquisitions, the accuracy of the scatter correction depends on the precision of the Monte Carlo codes. Despite the fact that MC simulations are gold-standard in the field and provide very realistic images, some works for scatter estimation in CT showed that the accuracy of a deep-learning model could decrease when applying a NN trained only with simulated images to a real image [19]. For CXRs, more studies are needed to determine the accuracy of neural networks in this situation. Since having a sufficient amount of cases to train only with real data is complex in this field, it would be convenient to get images as realistic as possible. For this purpose, if at least some real cases are available, the use of generative adversarial networks (GANs) [56] in combination with MC simulations could achieve this goal and thus improve the accuracy of the models applied to real data.
It is important to note that the input-output pairs of images of the neural network are exclusively uncorrected scatter–scatter ratio images. That is to say, the models are not trained to distinguish if the input image is affected by the scatter contribution, so if giving a scatter-free projection to the network, it will still yield some scatter estimation. The subtraction of this estimated image from a scatter-free input image would entail some loss of information in the final result. Therefore, these models cannot be applied to acquisitions taken with an anti-scatter grid or any other scatter suppression technique, neither can be used to check the effectiveness in scatter removal of those hardware-based scatter suppression methods. A neural network that identifies if the input image is affected by scattered rays is currently being implemented, but it is beyond the scope of this work.
As explained in Section 2.3, a ROI focus primarily on the lungs region was selected in the training, validation and test images (see Figure 1). This way, the edges of the images that could cause the appearance of artifacts in the scatter estimation and the scatter-corrected images are removed. This fact allows us to get very accurate results, but it must be taken into account before putting the models into practice. An input image with a large amount of empty regions could compromise the robustness of the models, just as it is suggested by the results obtained for images simulated SDD=200 cm.
Although the number of training and validation cases might seem small, the variety in the patient sizes within the dataset (explained in Section 2.1) along with the data augmentation described in Section 2.3 guarantees the accuracy of the models for images with different amounts of scatter ratio.
Regarding the study of the contrast improvement after scatter correction, in this work we focused on COVID-19 since a large number of databases related to this disease has been gathered in the past two years as a consequence of the worldwide pandemic. However, the same analysis could be performed for any other pulmonary affection, as pneumonia, tumors, atelectasis or pneumothorax. It is highly expected that the scatter correction will also entail a contrast improvement in areas affected by any of these lesions, and therefore facilitate its identification.
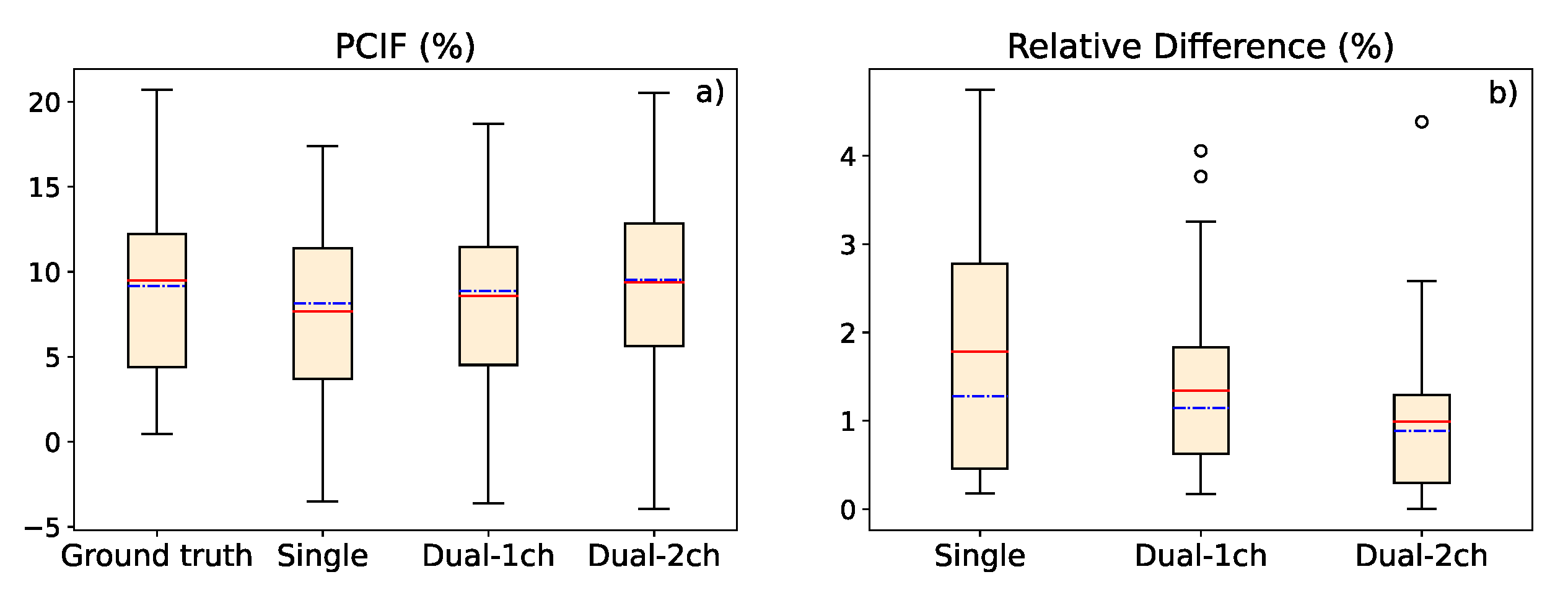
It should be taken into account that an overestimation in the contrast value could result in a loss of important information for medical diagnosis in the final scatter-corrected image. Results in Table A1 show that the contrast is overestimated in 7 out of 31 cases in the single-energy model, in 14 cases in the 1-output dual-energy model, and in 11 cases in the 2-output dual-energy model. Nevertheless, the difference with the ground truth value is on average just 1.11% for the single-energy method, 1.48% for the 1-output dual-energy network, and 1.01% for the 2-output dual-energy model. Thus, the overestimation is not significant and will not jeopardize the image information.

5. Conclusions

In this work, we presented three deep learning-based methods to estimate the scatter contribution in CXRs and obtain the scatter-corrected projections: a single-energy model, with one input and one output image; a 1-output dual-energy model, in which a projection acquired with a different energy spectrum is set as an additional input channel, but the output has only one channel; and a 2-output dual-energy model, in which the scatter estimation is provided for the two energies introduced in the two input channels. The three models were robust to variations in the SDD, obtaining a high precision for distances in a range between 100 and 200 cm, and proving that a similar accuracy with respect to images with the original SDD of the training data (SDD=180 cm) can be maintained. Besides, the contrast values between the lung region affected by COVID-19 and the healthy region in soft tissue images (obtained by means of dual energy subtraction) demonstrated that scatter correction in CXRs provides better contrast to the area of the lesion, yielding a PCIF of up to 20.5%.
In both studies (accuracy in scatter correction for several SDD and contrast value in COVID-19 region), the dual-energy algorithms provide results with a better accuracy. The analysis of the p-value points out that the difference in the accuracy between the single-energy and dual-energy models can be statistically significant, especially in the scatter-corrected estimations of high energy CXRs with the 2-output method. The single-energy algorithm is accurate enough for scatter correction of CXRs, so it might not be worthy to acquire an extra CXR just for this purpose. However, dual-energy models are proven to be a useful tool for scatter correction on soft tissue DES CXRs.
The single-energy model was tested with a cohort of real CXRs acquired without an anti-scatter grid, yielding robust, qualitative estimations of the scatter correction, even for images with artifacts. Further studies with real phantoms and patients should be performed to quantitatively determine the precision of the three models with real data, and to analyze whether the difference between the performance of the single and dual-energy algorithms is relevant.

Funding

This research was funded by the Spanish Ministry of Science and Innovation grant numbers PID2021-126998OB-I00, RTC2019-007112-1 XPHASE-LASER and PDC2022-133057-I00/AEI/10.13039/ 501100011033/ Unión Europea NextGenerationEU/PRTR grants. C. Freijo work was funded by a University Complutense of Madrid and Banco Santander predoctoral fellowship, CT82/20-CT83/20.

Data Availability Statement

The simulated CXR dataset and the neural networks code is publicly available at https://github.com/clarafreijo/CXR-Scatter-Correction.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. Contrast value (Equation 5) between the COVID-19 affected region and the healthy lung for the soft tissue test images in the uncorrected image, the scatter-corrected ground truth image and the scatter-corrected images estimated by the single-energy and dual-energy models. For patients with both lungs affected, each lung has been considered as a different case.
Table A1. Contrast value (Equation 5) between the COVID-19 affected region and the healthy lung for the soft tissue test images in the uncorrected image, the scatter-corrected ground truth image and the scatter-corrected images estimated by the single-energy and dual-energy models. For patients with both lungs affected, each lung has been considered as a different case.
Patient Ground truth uncorrected image Ground truth scatter-corrected image Scatter-corrected with single energy Scatter-corrected with 1-output dual energy Scatter-corrected with 2-output dual energy
Case 1 1.216 1.385 1.352 1.374 1.380
Case 2 1.165 1.282 1.268 1.285 1.278
Case 3 1.032 1.101 1.072 1.080 1.095
Case 4 1.292 1.430 1.419 1.404 1.455
Case 5 1.187 1.299 1.289 1.293 1.299
Case 6 1.047 1.018 1.045 1.048 1.014
Case 7 1.147 1.239 1.235 1.231 1.255
Case 8 1.297 1.448 1.453 1.439 1.434
Case 9 1.096 1.301 1.244 1.252 1.284
Case 10 1.301 1.553 1.499 1.531 1.526
Case 11 1.154 1.201 1.195 1.198 1.190
Case 12 1.045 1.159 1.104 1.145 1.149
Case 13 0.795 0.645 0.648 0.684 0.627
Case 14 1.209 1.454 1.403 1.434 1.436
Case 15 1.305 1.575 1.532 1.549 1.573
Case 16 1.128 1.176 1.170 1.198 1.184
Case 17 0.960 0.931 0.922 0.953 0.928
Case 18 1.104 1.202 1.173 1.205 1.213
Case 19 1.037 1.035 1.052 1.045 1.040
Case 20 0.879 0.890 0.864 0.861 0.913
Case 21 1.110 1.115 1.113 1.103 1.114
Case 22 1.021 1.056 1.054 1.063 1.058
Case 23 0.945 0.987 0.967 0.972 1.001
Case 24 1.098 1.165 1.148 1.163 1.162
Case 25 1.209 1.324 1.327 1.333 1.325
Case 26 1.183 1.279 1.293 1.287 1.291
Case 27 0.962 0.886 0.898 0.899 0.851
Case 28 0.841 0.719 0.719 0.723 0.717
Case 29 0.872 0.816 0.795 0.817 0.791
Case 30 0.908 0.912 0.876 0.875 0.872
Case 31 1.316 1.532 1.529 1.562 1.544

References

  1. Candemir, S.; Antani, S. A review on lung boundary detection in chest x-rays. IJCARS 2019, 14, 563–576. [Google Scholar] [CrossRef]
  2. Gange, C.P.; Pahade, J.K.; Cortopassi, I.; Bader, A.S.; Bokhari, J.; Hoerner, M.; Thomas, K.M.; Rubinowitz, A.N. Social distancing with portable chest radiographs during the COVID-19 pandemic: assessment of radiograph technique and image quality obtained at 6 feet and through glass. Radiol.: Cardiothorac. Imaging 2020, 2, e200420. [Google Scholar] [CrossRef] [PubMed]
  3. Çallı, E.; Sogancioglu, E.; van Ginneken, B.; van Leeuwen, K.G.; Murphy, K. Deep learning for chest X-ray analysis: A survey. Med Image Anal. 2021, 72, 102125. [Google Scholar] [CrossRef] [PubMed]
  4. Raoof, S.; Feigin, D.; Sung, A.; Raoof, S.; Irugulpati, L.; Rosenow III, E.C. Interpretation of plain chest roentgenogram. Chest 2012, 141, 545–558. [Google Scholar] [CrossRef] [PubMed]
  5. Shaw, D.; Crawshaw, I.; Rimmer, S. Effects of tube potential and scatter rejection on image quality and effective dose in digital chest X-ray examination: an anthropomorphic phantom study. Radiography 2013, 19, 321–325. [Google Scholar] [CrossRef]
  6. Jones, J.; Murphy, A.; Bell, D. Chest radiograph. Available online: https://doi.org/10.53347/rID-14511 (accessed on 07 02 2023). [CrossRef]
  7. Mentrup, D.; Neitzel, U.; Jockel, S.; Maack, H.; Menser, B. Grid-like contrast enhancement for bedside chest radiographs acquired without anti-scatter grid. Philips SkyFlow 2014. [Google Scholar]
  8. Seibert, J.A.; Boone, J.M. X-ray imaging physics for nuclear medicine technologists. Part 2: X-ray interactions and image formation. J. Nucl. Med. Technol. 2005, 33, 3–18. [Google Scholar] [PubMed]
  9. Lee, H.; Lee, J. A deep learning-based scatter correction of simulated X-ray images. Electronics 2019, 8, 944. [Google Scholar] [CrossRef]
  10. Liu, X.; Shaw, C.C.; Lai, C.J.; Wang, T. Comparison of scatter rejection and low-contrast performance of scan equalization digital radiography (SEDR), slot-scan digital radiography, and full-field digital radiography systems for chest phantom imaging. Med. Phys. 2011, 38, 23–33. [Google Scholar] [CrossRef]
  11. Rührnschopf, E.P.; Klingenbeck, K. A general framework and review of scatter correction methods in X-ray cone-beam computerized tomography. Part 1: scatter compensation approaches. Med. Phys. 2011, 38, 4296–4311. [Google Scholar] [CrossRef]
  12. Chan, H.P.; Lam, K.L.; Wu, Y. Studies of performance of antiscatter grids in digital radiography: Effect on signal-to-noise ratio. Med. Phys. 1990, 17, 655–664. [Google Scholar] [CrossRef] [PubMed]
  13. Roser, P.; Birkhold, A.; Preuhs, A.; Syben, C.; Felsner, L.; Hoppe, E.; Strobel, N.; Kowarschik, M.; Fahrig, R.; Maier, A. X-ray scatter estimation using deep splines. IEEE Trans. Med. Imaging 2021, 40, 2272–2283. [Google Scholar] [CrossRef] [PubMed]
  14. Gauntt, D.M.; Barnes, G.T. Grid line artifact formation: A comprehensive theory. Med. Phys. 2006, 33, 1668–1677. [Google Scholar] [CrossRef] [PubMed]
  15. Bernhardt, T.; Rapp-Bernhardt, U.; Hausmann, T.; Reichel, G.; Krause, U.; Doehring, W. Digital selenium radiography: anti-scatter grid for chest radiography in a clinical study. Brit. J. Radiol. 2000, 73, 963–968. [Google Scholar] [CrossRef] [PubMed]
  16. Roberts, J.; Evans, S; Rees, M. Optimisation of imaging technique used in direct digital radiography. J. Radiol. Prot. 2006, 26, 287. [Google Scholar] [CrossRef] [PubMed]
  17. Moore, C.; Avery, G.; Balcam, S.; Needler, L.; Swift, A.; Beavis, A.; Saunderson, J. Use of a digitally reconstructed radiograph-based computer simulation for the optimisation of chest radiographic techniques for computed radiography imaging systems. Brit. J. Radiol. 2012, 85, e630–e639. [Google Scholar] [CrossRef] [PubMed]
  18. Lifton, J.; Malcolm, A.; McBride, J. An experimental study on the influence of scatter and beam hardening in X-ray CT for dimensional metrology. Meas. Sci. Technol. 2015, 27, 015007. [Google Scholar] [CrossRef]
  19. Maier, J.; Sawall, S.; Knaup, M.; Kachelrieß, M. Deep scatter estimation (DSE): Accurate real-time scatter estimation for X-ray CT using a deep convolutional neural network. J. Nondestruct. Eval. 2018, 37, 1–9. [Google Scholar] [CrossRef]
  20. Swindell, W.; Evans, P.M. Scattered radiation in portal images: a Monte Carlo simulation and a simple physical model. Med. Phys. 1996, 23, 63–73. [Google Scholar] [CrossRef]
  21. Bhatia, N.; Tisseur, D.; Buyens, F.; Létang, J.M. Scattering correction using continuously thickness-adapted kernels. NDT E Int. 2016, 78, 52–60. [Google Scholar] [CrossRef]
  22. Codella, N.C.; Gutman, D.; Celebi, M.E.; Helba, B.; Marchetti, M.A.; Dusza, S.W.; Kalloo, A.; Liopyris, K.; Mishra, N.; Kittler, H.; et al. Skin lesion analysis toward melanoma detection: A challenge at the 2017 international symposium on biomedical imaging (ISBI), hosted by the international skin imaging collaboration (ISIC). In Proceedings of 2018 IEEE 15th international symposium on biomedical imaging (ISBI 2018), Washington D.C., USA; 04 04 2018. [Google Scholar]
  23. Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; LeCun, Y. Overfeat: Integrated recognition, localization and detection using convolutional networks. arXiv preprint arXiv:1312.6229 2013.
  24. Rouhi, R.; Jafari, M.; Kasaei, S.; Keshavarzian, P. Benign and malignant breast tumors classification based on region growing and CNN segmentation. Expert Syst. Appl. 2015, 42, 990–1002. [Google Scholar] [CrossRef]
  25. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
  26. Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany; 05 10 2015. [Google Scholar]
  27. Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-net and its variants for medical image segmentation: A review of theory and applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
  28. Ibtehaz, N.; Rahman, M.S. MultiResUNet: Rethinking the U-Net architecture for multimodal biomedical image segmentation. Neural Netw. 2020, 121, 74–87. [Google Scholar] [CrossRef] [PubMed]
  29. Alvarez, R.E.; Macovski, A. Energy-selective reconstructions in X-ray computerised tomography. Phys. Med. Biol. 1976, 21, 733. [Google Scholar] [CrossRef] [PubMed]
  30. Sellerer, T.; Mechlem, K.; Tang, R.; Taphorn, K.A.; Pfeiffer, F.; Herzen, J. Dual-energy X-ray dark-field material decomposition. IEEE Trans. Med. Imaging 2020, 40, 974–985. [Google Scholar] [CrossRef] [PubMed]
  31. Fredenberg, E. Spectral and dual-energy X-ray imaging for medical applications. Nucl. Instrum. Methods Phys. Res. A 2018, 878, 74–87. [Google Scholar] [CrossRef]
  32. Martz, H.E.; Glenn, S.M. Dual-energy X-ray radiography and computed tomography. Technical Report, Lawrence Livermore National Lab.(LLNL), Livermore, CA (United States), 2019.
  33. Marin, D.; Boll, D.T.; Mileto, A.; Nelson, R.C. State of the art: Dual-energy CT of the abdomen. Radiology 2014, 271, 327–342. [Google Scholar] [CrossRef] [PubMed]
  34. Manji, F.; Wang, J.; Norman, G.; Wang, Z.; Koff, D. Comparison of dual energy subtraction chest radiography and traditional chest X-rays in the detection of pulmonary nodules. Quant. Imaging. Med. Surg. 2016, 6, 1. [Google Scholar]
  35. Vock, P.; Szucs-Farkas, Z. Dual energy subtraction: principles and clinical applications. Eur. J. Radiol. 2009, 72, 231–237. [Google Scholar] [CrossRef]
  36. Yang, F.; Weng, X.; Miao, Y.; Wu, Y.; Xie, H.; Lei, P. Deep learning approach for automatic segmentation of ulna and radius in dual-energy X-ray imaging. Insights Imaging 2021, 12, 1–9. [Google Scholar] [CrossRef]
  37. Luo, R.; Ge, Y.; Hu, Z.; Liang, D.; Li, Z.C. DeepPhase: Learning phase contrast signal from dual energy X-ray absorption images. Displays 2021, 69, 102027. [Google Scholar] [CrossRef]
  38. Lee, D.; Kim, H.; Choi, B.; Kim, H.J. Development of a deep neural network for generating synthetic dual-energy chest X-ray images with single X-ray exposure. Phys. Med. Biol. 2019, 64, 115017. [Google Scholar] [CrossRef]
  39. Roth, H.R.; Xu, Z.; Tor-Díez, C.; Jacob, R.S.; Zember, J.; Molto, J.; Li, W.; Xu, S.; Turkbey, B.; Turkbey, E.; et al. Rapid artificial intelligence solutions in a pandemic – The COVID-19-20 lung CT lesion segmentation challenge. Med Image Anal. 2022, 82, 102605. [Google Scholar] [CrossRef] [PubMed]
  40. Schneider, U.; Pedroni, E.; Lomax, A. The calibration of CT Hounsfield units for radiotherapy treatment planning. Phys. Med. Biol. 1996, 41, 111. [Google Scholar] [CrossRef]
  41. Ibáñez, P.; Villa-Abaunza, A.; Vidal, M.; Guerra, P.; Graullera, S.; Illana, C.; Udías, J.M. XIORT-MC: A real-time MC-based dose computation tool for low-energy X-rays intraoperative radiation therapy. Med. Phys. 2021, 48, 8089–8106. [Google Scholar] [CrossRef] [PubMed]
  42. Punnoose, J.; Xu, J.; Sisniega, A.; Zbijewski, W.; Siewerdsen, J. Technical note: spektr 3.0–A computational tool for x-ray spectrum. Med. Phys. 2016, 43, 4711–4717. [Google Scholar] [CrossRef]
  43. Sisniega, A.; Desco, M.; Vaquero, J. Modification of the tasmip X-ray spectral model for the simulation of microfocus X-ray sources. Med. Phys. 2014, 41, 011902. [Google Scholar] [CrossRef] [PubMed]
  44. Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of International Conference on Machine Learning, Lille, France; 06 07 2015. [Google Scholar]
  45. Hara, K.; Saito, D.; Shouno, H. Analysis of function of rectified linear unit used in deep learning. In Proceedings of 2015 International joint conference on neural networks (IJCNN), Killarney, Ireland; 12 07 2015. [Google Scholar]
  46. Carneiro, T.; Da Nóbrega, R.V.M.; Nepomuceno, T.; Bian, G.B.; De Albuquerque, V.H.C.; Reboucas Filho, P.P. Performance analysis of google colaboratory as a tool for accelerating deep learning applications. IEEE Access 2018, 6, 61677–61685. [Google Scholar] [CrossRef]
  47. Bisong, E. Building machine learning and deep learning models on Google Cloud platform; Springer: 2019.
  48. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 2014.
  49. Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
  50. Avanaki, A.N. Exact global histogram specification optimized for structural similarity. Opt. Rev. 2009, 16, 613–621. [Google Scholar] [CrossRef]
  51. Johnson, A.; Pollard, T.; Mark, R.; Berkowitz, S.; Horng, S. Mimic-CXR database. PhysioNet10 2019, 13026, C2JT1Q. [Google Scholar]
  52. Johnson, A.E.; Pollard, T.J.; Berkowitz, S.J.; Greenbaum, N.R.; Lungren, M.P.; Deng, C.Y.; Mark, R.G.; Horng, S. Mimic-CXR, a de-identified publicly available database of chest radiographs with free-text reports. Sci. Data 2019, 6, 317. [Google Scholar] [CrossRef] [PubMed]
  53. Swinehart, D.F. The Beer-Lambert law. J. Chem. Educ. 1962, 39, 333. [Google Scholar] [CrossRef]
  54. Benjamin, D.J.; Berger, J.O.; Johannesson, M.; Nosek, B.A.; Wagenmakers, E.J.; Berk, R.; Bollen, K.A.; Brembs, B.; Brown, L.; Camerer, C.; et al. Redefine statistical significance. Nat. Hum. Behav. 2018, 2, 6–10. [Google Scholar] [CrossRef] [PubMed]
  55. Di Leo, G.; Sardanelli, F. Statistical significance: p value, 0.05 threshold, and applications to radiomics–reasons for a conservative approach. Eur. Radiol. Exp. 2020, 4, 1–8. [Google Scholar] [CrossRef]
  56. Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
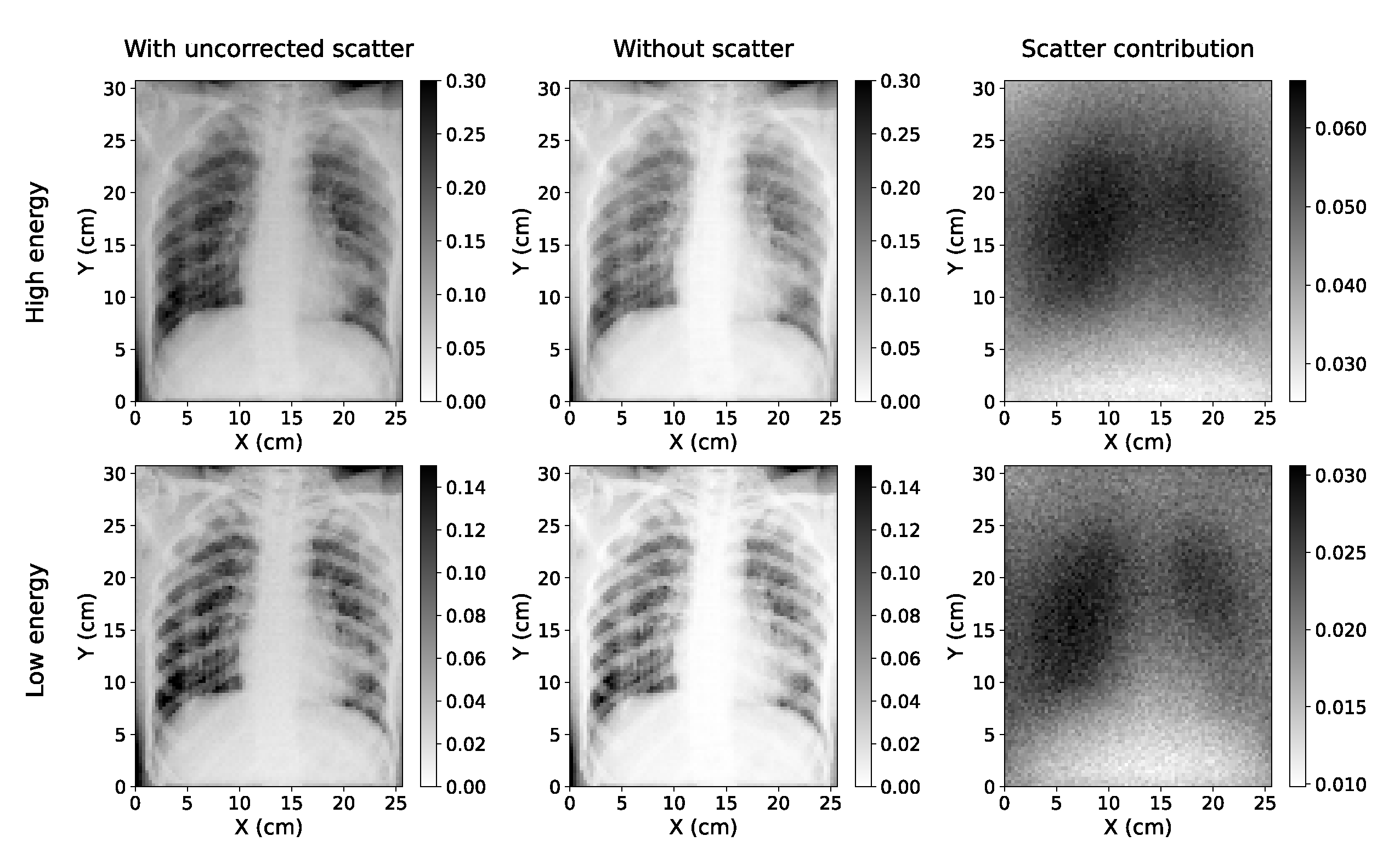
Preprints 90589 g001
Figure 1. Simulated Chest X-rays for two cases considered (low energy=60 kVp; high energy=130 kVp). The simulation with scatter (left) can be decomposed into a direct component ("without scatter", center) and the scatter contribution (right).
Figure 1. Simulated Chest X-rays for two cases considered (low energy=60 kVp; high energy=130 kVp). The simulation with scatter (left) can be decomposed into a direct component ("without scatter", center) and the scatter contribution (right).
Preprints 90589 g001
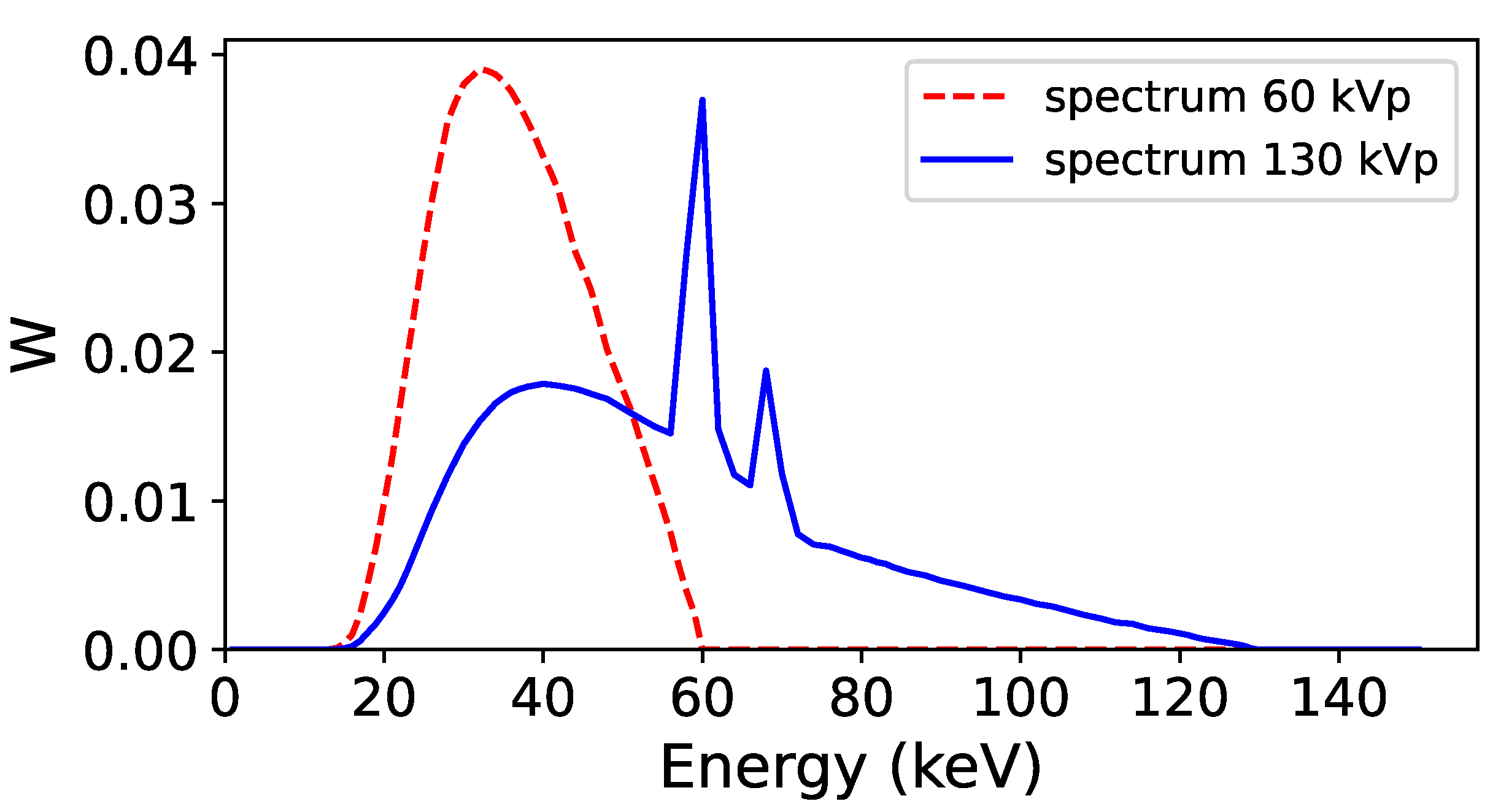
Preprints 90589 g002
Figure 2. Energy spectra used to acquire the low energy (60 kVp, red line) and high energy (130 kVp, blue line) projections in the Monte Carlo simulation. The two spectra were obtained with Specktr toolkit [42,43], with 1.6 mm Al inherent filtration of the tube.
Figure 2. Energy spectra used to acquire the low energy (60 kVp, red line) and high energy (130 kVp, blue line) projections in the Monte Carlo simulation. The two spectra were obtained with Specktr toolkit [42,43], with 1.6 mm Al inherent filtration of the tube.
Preprints 90589 g002
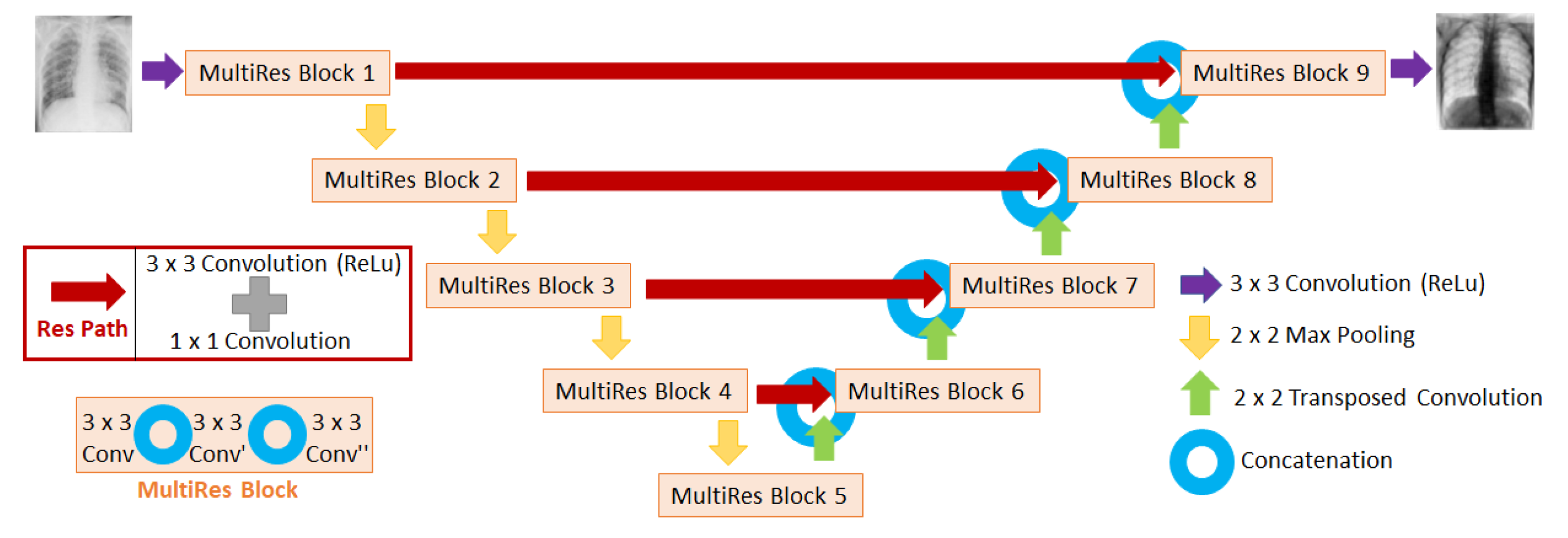
Preprints 90589 g003
Figure 3. Diagram of the MultiResUNet architecture used in this work to train the neural networks. The input of the network is the image affected by scatter (i.e. uncorrected scatter image), and the output is the fraction of the image of scatter with respect to the uncorrected scatter image.
Figure 3. Diagram of the MultiResUNet architecture used in this work to train the neural networks. The input of the network is the image affected by scatter (i.e. uncorrected scatter image), and the output is the fraction of the image of scatter with respect to the uncorrected scatter image.
Preprints 90589 g003
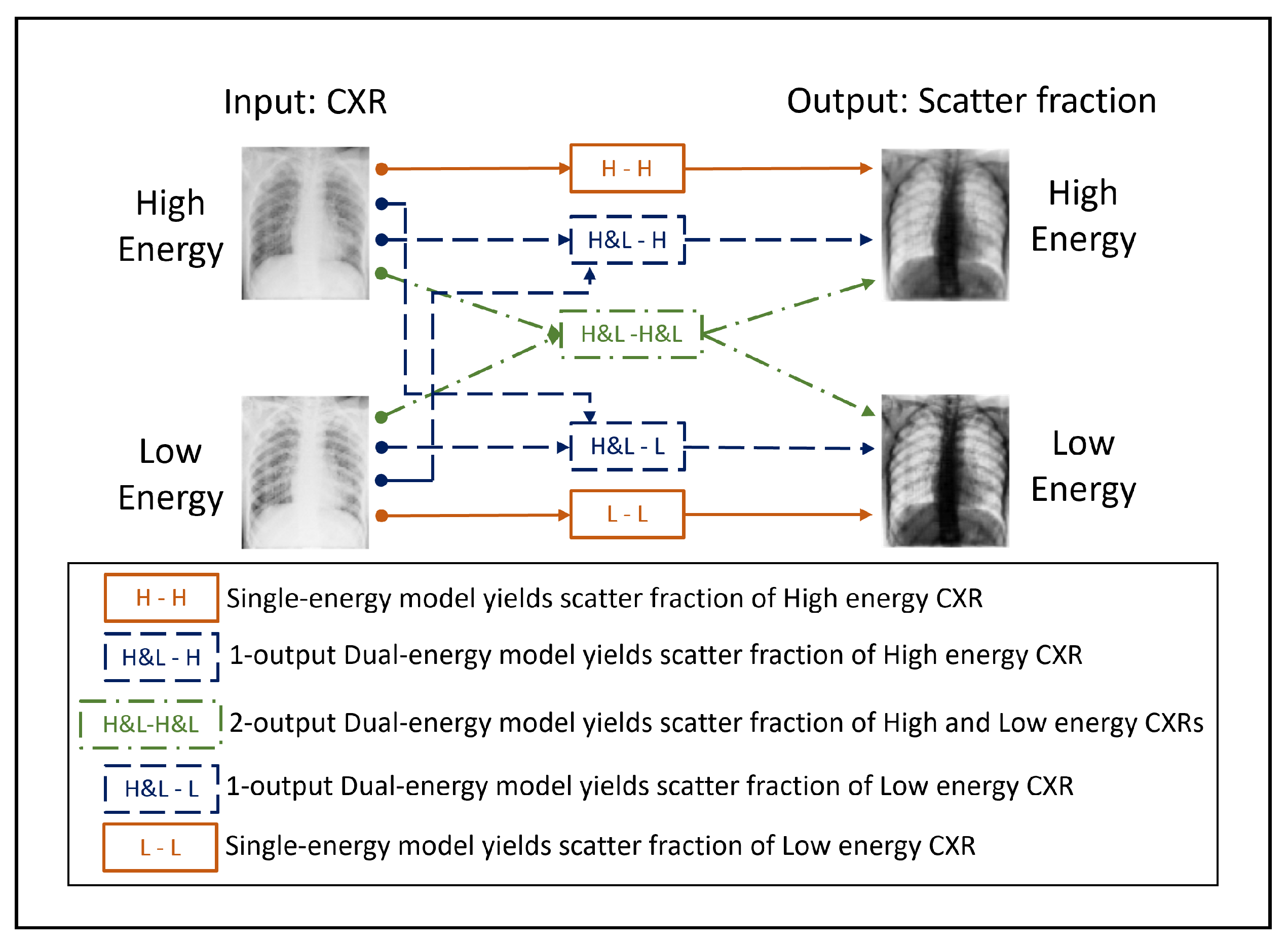
Preprints 90589 g004
Figure 4. Scheme of the input and output images corresponding to the 3 neural network models presented in this work. The NNs differ on the amount of input and output channels used.
Figure 4. Scheme of the input and output images corresponding to the 3 neural network models presented in this work. The NNs differ on the amount of input and output channels used.
Preprints 90589 g004
Preprints 90589 g005
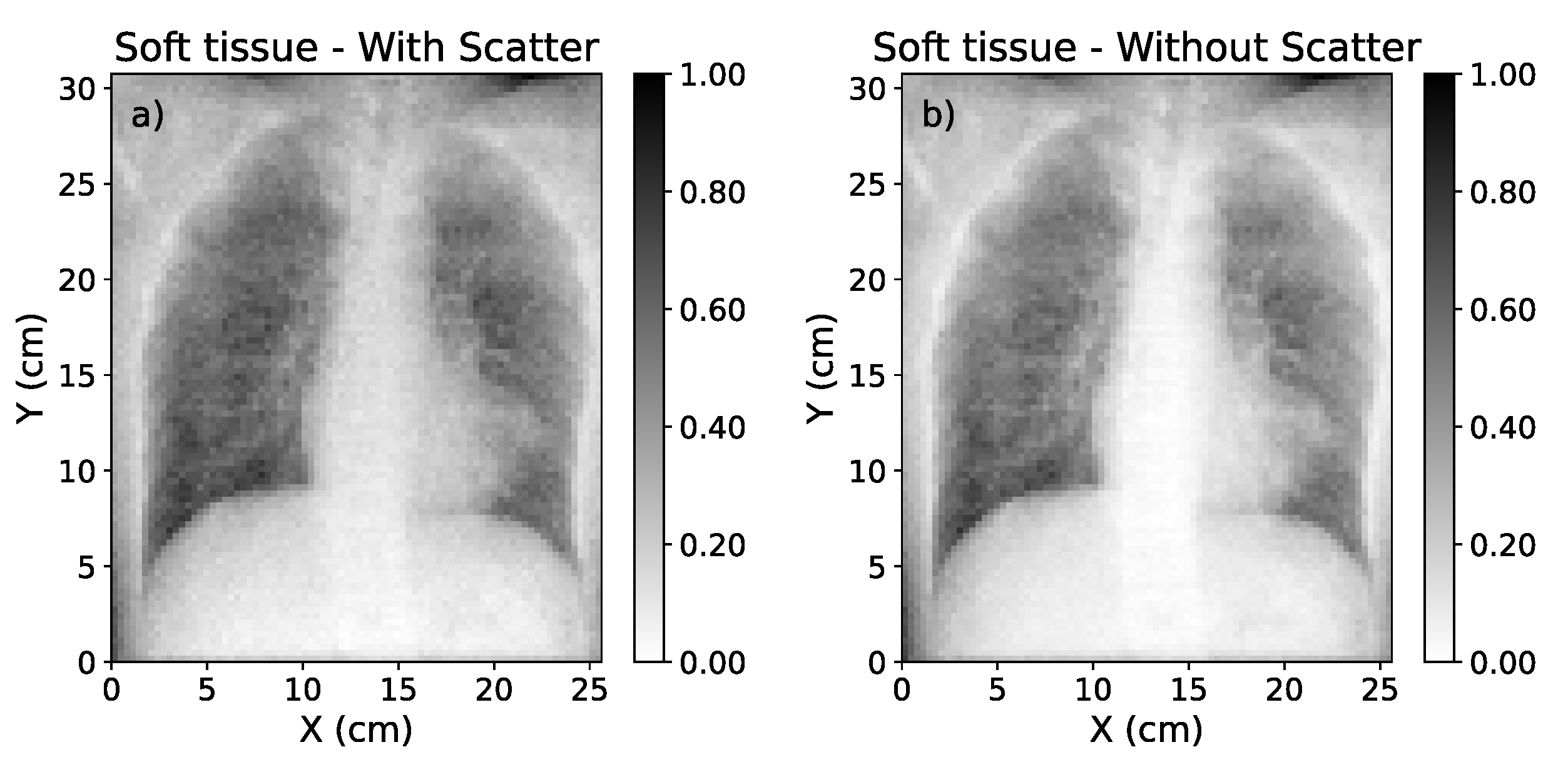
Figure 5. Soft tissue dual energy subtraction images: (a) Calculated from uncorrected-scatter CXRs of 60 kVp and 130 kVp. (b) Calculated from ground-truth scatter corrected images of 60 kVp and 130 kVp.
Figure 5. Soft tissue dual energy subtraction images: (a) Calculated from uncorrected-scatter CXRs of 60 kVp and 130 kVp. (b) Calculated from ground-truth scatter corrected images of 60 kVp and 130 kVp.
Preprints 90589 g005
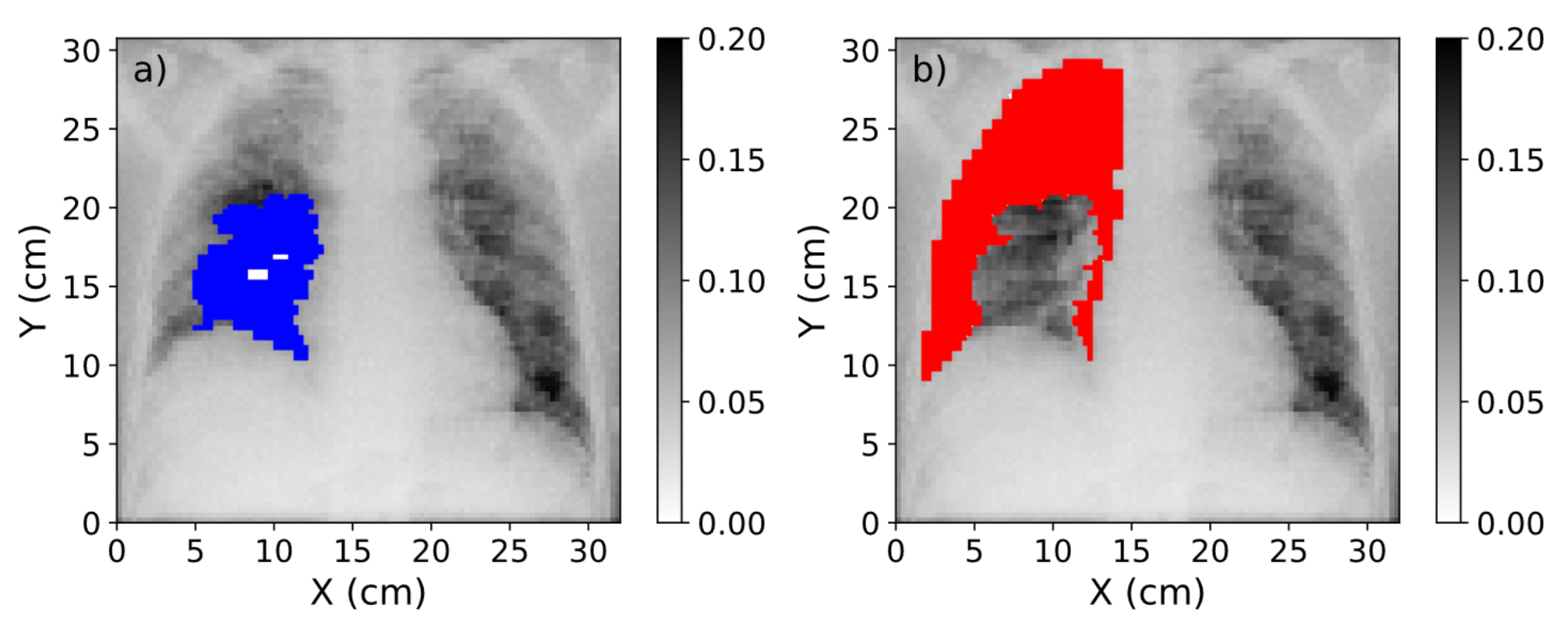
Preprints 90589 g006
Figure 6. (a) Mask of the region affected by COVID-19 (blue) over the CXR. (b) Mask of the healthy region in the lung (red). The range of values of these images was obtained after the normalization procedure explained in Section 2.2.
Figure 6. (a) Mask of the region affected by COVID-19 (blue) over the CXR. (b) Mask of the healthy region in the lung (red). The range of values of these images was obtained after the normalization procedure explained in Section 2.2.
Preprints 90589 g006
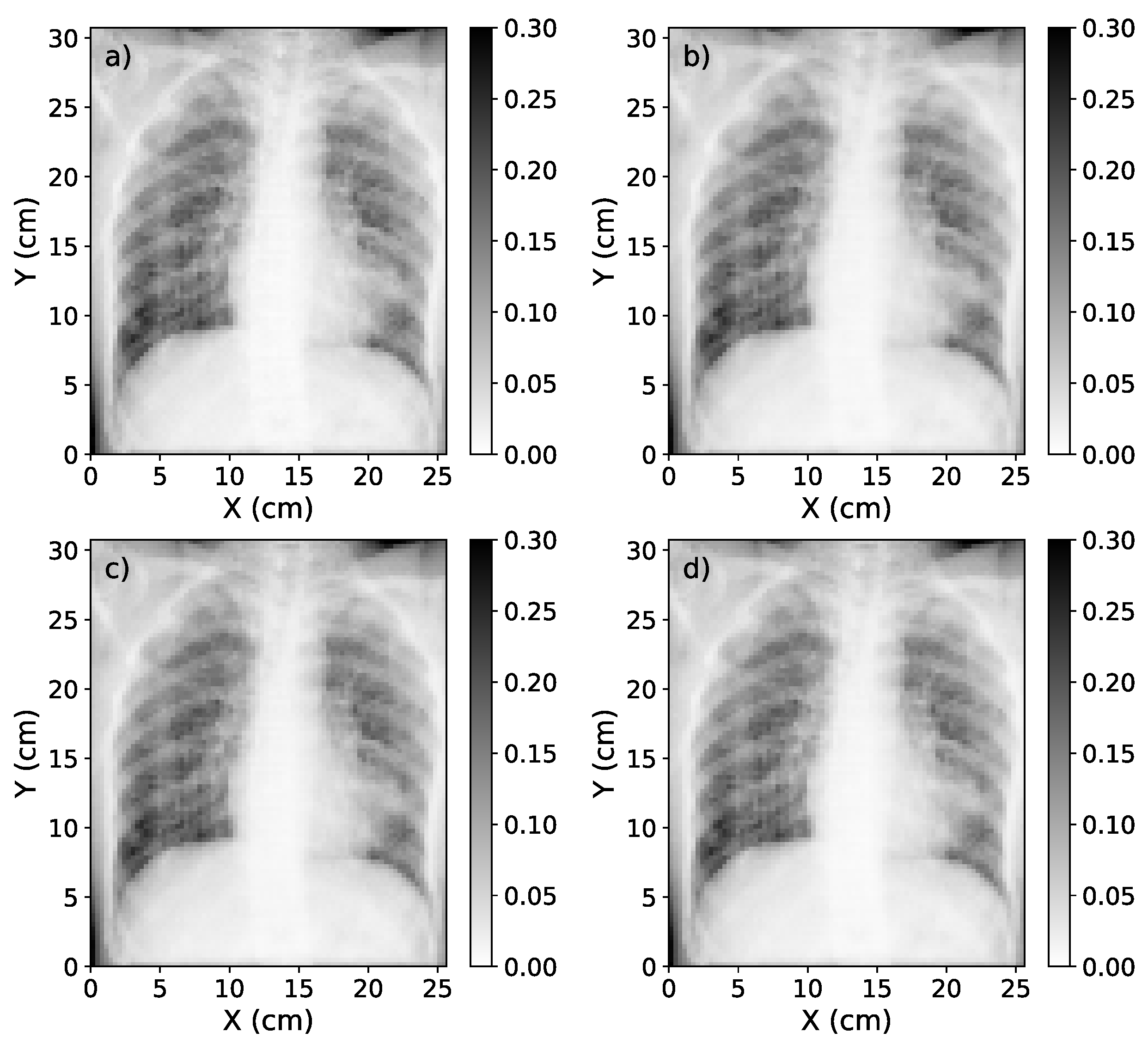
Preprints 90589 g007
Figure 7. (a) Representation of the scatter-corrected ground truth image. (b) The scatter-corrected image estimated by the single-energy model. (c) The scatter-corrected image estimated by the 1-output dual-energy model. (d) The scatter-corrected image estimated by the 2-output dual-energy model.
Figure 7. (a) Representation of the scatter-corrected ground truth image. (b) The scatter-corrected image estimated by the single-energy model. (c) The scatter-corrected image estimated by the 1-output dual-energy model. (d) The scatter-corrected image estimated by the 2-output dual-energy model.
Preprints 90589 g007
Preprints 90589 g008
Figure 8. Box plot of the MSE, MAPE, SSIM and relative error for the 22 test cases at different source-to-detector distances. Blue, dashed line represents the median value of the metric for each SDD. The box extends from the lower to the upper quartile values of the data, while the range (also referred to as whiskers) shows the rest of the distribution.
Figure 8. Box plot of the MSE, MAPE, SSIM and relative error for the 22 test cases at different source-to-detector distances. Blue, dashed line represents the median value of the metric for each SDD. The box extends from the lower to the upper quartile values of the data, while the range (also referred to as whiskers) shows the rest of the distribution.
Preprints 90589 g008
Preprints 90589 g009
Figure 9. a) Graphic representation of the percentage contrast improvement factor for ground truth image, single-energy model estimation, 1-output dual-energy model and 2-output dual-energy model estimation. (b) Relative difference in the contrast value between ground truth and deep learning-based estimations. In both graphics, the red, solid line represents the average value, while the blue, dash-dotted line represents the median value.
Figure 9. a) Graphic representation of the percentage contrast improvement factor for ground truth image, single-energy model estimation, 1-output dual-energy model and 2-output dual-energy model estimation. (b) Relative difference in the contrast value between ground truth and deep learning-based estimations. In both graphics, the red, solid line represents the average value, while the blue, dash-dotted line represents the median value.
Preprints 90589 g009
Preprints 90589 g010
Figure 10. Original CXR (with scatter) with pixel value conversion (left); estimation of the scatter-corrected CXR (center); and estimation of the scatter contribution on real CXR (right) of three of the real chest X-ray images used to test the single-energy model of scatter correction.
Figure 10. Original CXR (with scatter) with pixel value conversion (left); estimation of the scatter-corrected CXR (center); and estimation of the scatter contribution on real CXR (right) of three of the real chest X-ray images used to test the single-energy model of scatter correction.
Preprints 90589 g010
Table 1. Parameters of the MC simulation.
Table 1. Parameters of the MC simulation.
Parameter Specification
Source-Detector Distance (cm) 180
X-ray Detector Size (cm) 41 × 41
X-ray Detector Resolution (pixel) 2050 × 2050
Table 2. Ratio between a region of the lung with and without rib in the original, real CXRs and in the scatter-corrected CXRs yielded by the single-energy algorithm for the 10 CXRs taken as test set (listed as C1-C10), and the resulting average value.
Table 2. Ratio between a region of the lung with and without rib in the original, real CXRs and in the scatter-corrected CXRs yielded by the single-energy algorithm for the 10 CXRs taken as test set (listed as C1-C10), and the resulting average value.
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 Avg
Original 2.71 1.66 1.36 1.11 1.35 1.16 1.71 1.47 1.28 1.59 1.54
Scatter-corrected 3.80 2.02 1.54 1.17 1.49 1.23 2.14 1.68 1.41 1.64 1.81
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated