Prerpints.org logo
Preprint
Article

Monitoring Braided River-Bed Dynamics at Sub-Event Time Scale Using Time Series of Sentinel-1 SAR Imagery

Altmetrics

Downloads

126

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 June 2023

Posted:

08 June 2023

You are already at the latest version

Alerts
Abstract
Remote sensing plays a central role in the assessment of environmental phenomena and has increasingly become a powerful tool for monitoring shorelines, rivers morphology, flood waves delineation and floods assessment. Optical based monitoring and characterization of river evolution at long time scales is a key tool in fluvial geomorphology. However, the evolution occurring during extreme events is crucial for the understanding of the river dynamics under severe flow conditions and requires the processing of data from active sensors to overcome cloud obstructions. This work proposes a cloud-based unsupervised algorithm for the intra-event monitoring of river dynamics during extreme flow conditions based on time series of Sentinel-1 SAR data. The method allows the extraction of multi-temporal series of spatially explicit geometric parameters at high time and spatial resolutions, linking them to the hydrometric levels acquired by reference gauge stations. Intra-event reconstruction of inundation dynamics has led to the estimation of the relationship between hydrometric level and wet area extension and the assessment of bank erosion phenomena. Time series of SAR acquisitions, provided by Copernicus Sentinel-1 satellites, were analyzed to quantify changes in the wet area of a reach of the Tagliamento river under different flow conditions. The algorithm, developed within the Python-API of GEE, first empowers the Sentinel-1 images with the hydrometric level, then involves radiometric slope correction and speckle noise filtering. The Otsu method is then used for image segmentation leading to a water and dry land binary classification. Results support many types of analysis about river dynamics, including morphological changes, floods monitoring and relief efforts and bio-physical habitat dynamics. The results encourage future advancements and applications of the algorithm, specifically exploring SAR data from ICEYE and Capella Space constellations, which offer significantly higher spatial and temporal resolutions compared to Sentinel-1 data.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Rivers and their floodplains are among the most complex, dynamic, and diverse ecosystems on Earth, providing major economic, health, cultural, scientific, and educational ecosystem services [1,2]. Despite accounting for just 1.4% of the land surface area, riparian zones provide at least 25% of all terrestrial ecosystem services [3]. Rivers’ dynamic behavior originates from the continuous interaction between variable flow, sediment transport and associated morphological change, and ecological feedback mainly through aquatic and riparian vegetation [4,5]. Most of these dynamic processes occur during floods, which are characterized by the increase of flowing discharge, often associated with a large widening of the inundated areas, both inside the active channel and in adjacent zones. The possibility to understand, quantify and predict river evolution strongly depends on our ability to monitor what happens during these events, which in some cases last for only a few hours or days, but can shape the riverbed morphology for the following months and years [6,7]. An accurate monitoring of rivers and floodplains dynamics is therefore crucial to enhance river management and, at European level, to meet the objectives of the Water Framework and Flood Directives (2000/60/EC [8] and 2007/60/EC [9]).
In the last decade, advances in remote sensing technologies and the computational ability to process vast data-sets are increasing at unprecedented speed and have revolutionized the way we quantify and assess river systems [10] offering new sources of high resolution, multidimensional data across wide spatial scales and at multiple time scales, towards a data-rich geomorphological science [11]. The availability of different satellite imagery, often freely accessible, can be coupled with various cloud computing platforms and distributed systems such as Google Earth Engine (GEE), Sentinel Hub, Open Data Cube, openEO, and others [12].
Satellite imagery, and in particular the freely available Landsat and Sentinel-2 multi-spectral images were successfully used for river mapping since the ‘90s [13], with continuous improvements since, towards an accurate evaluation of channel width [14], river centerline and sinuosity [15] and more in general for mapping surface water extent and dynamics [16,17,18].
However, approaches based on optical data in the visible and near-infrared range suffer from strong limitations due to the adverse atmospheric conditions that often characterize flood events. Particularly in the case of relatively small catchments (areas smaller than 10 4 – 10 5 k m 2 ), flood peaks occur shortly after raining events, implying that cloud coverage is very likely to persist, reducing the possibility to effectively monitor large river areas. On the contrary, satellites carrying active radar sensors operating in the microwave range are not affected by cloud coverage and therefore provide an attractive way to remotely track the dynamics of rapidly changing river systems. Indeed Synthetic Aperture Radar (SAR) permits an all-weather and all-time monitoring, playing a decisive role in the detection of large flooded areas [19,20,21,22,23], with applications on freshwater lakes [24], on monitoring of river morphology [25,26], and on extraction of river networks [27,28] even in the case of complex braided rivers [29].
In this work we i) develop an unsupervised and cloud-based algorithm for the analysis of stack SAR images, and ii) include water flow level information through metadata enrichment, with the objective to automatically extract and monitor the inundation dynamics at sub-event temporal scale. The algorithm is then tested and verified on a 13-km long reach of the Tagliamento River (Italy), a large, braided gravel bed river, recognized as the most natural and dynamic large river in the European Alps. Furthermore, the availability of imagery at sub-event time scale, as opposed to the standard before-after flood approach, allows the observation and quantification of lateral bank erosion and channel dynamics, during the flood event and with accurate timing as a function of water level and inundation duration. The paper is organized as follows: Section 2 presents the theoretical approach, and describes the details of the computation steps and the dataset; Section 3 illustrates the case study and Section 4 shows the results on mapping river inundated areas and morphological change during the flood events occurred from 2018 to 2020. Discussion on perspective and limitations of the present work, along with the geomorphological significance and main concluding remarks are provided in Section 5.

2. Materials and methods

This work proposes an unsupervised methodology based on the Google Earth Engine cloud infrastructure for the continuous monitoring of river dynamics during flood events. The processing chain implements the following steps:
  • enriching the image stack with hydrometric data;
  • applying the radiometric slope correction algorithm;
  • reducing speckle noise;
  • extracting the wet channel with a thresholding algorithm;
  • output functions.
Each function was structured in a main body and sub-functions with the purpose of allowing sequential calls needed from the time series of images.
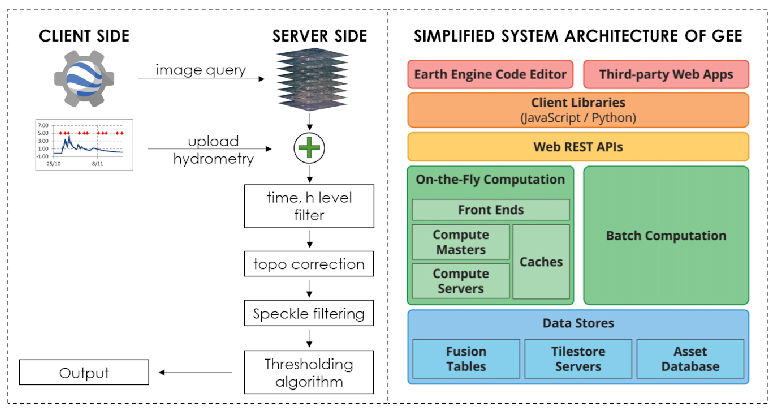
GEE’s architecture is based on a Client/Server programming model (Figure 1, right panel). Under this architecture, the client libraries provide a user-friendly programming environment, recording the computational chain and sending it to the server for the execution. This implies that it’s impossible to combine Earth Engine library calls (server side) with local processing operations (client side). The procedure has three points where client site and server side exchange inputs and outputs: the image query step, the upload of hydrometric data and the output step which can save scatter plots, time series of water masks and data dictionaries (Figure 1, left panel).
The proposed method uses Level 1 (L1) - GRD product acquired in the Interferometric Wide swath (IW) mode from Sentinel-1. Sentinel-1 has a C-band sensor operating at a center frequency of 5.405 GHz (corresponding to a wavelength of ≈ 5.5 cm). IW product is Sentinel-1’s primary operational mode over land and it’s available in dual polarization, namely vertical emitted - vertically received (VV) or vertical emitted - horizontally received (VH). The vertical polarization, interacting with earth surface, can return to the satellite sensor in the vertical plane or in the horizontal one. Previous research showed that, in cases of non-windy conditions and no stream water, VV polarization results in higher accuracy than VH polarization [31], as VV polarization is sensitive to water surface roughness. VH is generated from the interaction with the tree crowns (volumetric scattering), and part of the backscatter is redirected towards the water channel causing misclassification [32]. In case of large gravel bed rivers without vegetation in the active channel, the rippling water surface of the river prevents the exploitation of VV polarization, suggesting to use the VH one. Before any analysis, the Sentinel-1 Ground Range Detected (GRD) product requires standard pre-processing, which involves updating the orbit information, removing the image border noise, modeling the thermal noise and thus calibrating radiometrically the images and applying the terrain correction. Google applies these corrections before ingesting the imagery in the Engine’s database.

2.1. Image selection and metadata enrichment

Images are selected on the basis of a spatial query with the region of interest and a query on the time interval of the flood event. After the initial image query, the metadata of the images are enriched with the hydrometric level registered at the time of image acquisition. This operation is crucial for the subsequent analysis, because it allows the determination of inundation dynamics joined with hydrometric levels.
The water level time series, composed of the date in string format and the water level in decimal floating-point format, are firstly converted into a collection of images and then joined with the SAR image collection. The resulting collection contains paired elements composed of the metadata and all the bands of the primary SAR collection and the matching element from the hydrometric level collection. The matching criterion is time dependent and SAR images are associated with the nearest water level value according to the following expression:
Pixel = h i i f t S A R ∈ [ t i ; t i + 1 / 2 ) h i + 1 i f t S A R ∈ [ t i + 1 / 2 ; t i + 1 ]
where h i and h i + 1 correspond to the water level at the time t i and t i + 1 respectively, t S A R is the SAR acquisition time and t i + 1 / 2 = ( t i + t i + 1 ) / 2 .

2.2. Radiometric terrain correction

Due to the side looking configuration of SAR sensors, there are a number of geometric and radiometric distortions that need correction and reduction. In the ideal case of a flat surface, the distortion is a specific geometric compression of the ground in the slant range, with distortion increasing moving from the furthest to the nearest range area. The conversion of slant range to ground range is normally done by the radar processor before the image creation and it enables true distance measurements.
Terrain slopes cause significant variations (radiometric distortions) on radar backscatter values, depending on the angle and aspect of the surface and on the radar configuration, in terms of frequency, polarization, and ascending or descending path. Foreshortening, layover and shadowing can be included among these effects. The first two happen when the slope is facing towards the sensor, while shadowing occurs on the opposite side. Foreshortening occurs when the slope in the range direction ( α r ) is less than the incidence angle ( θ i ), whereas layover appears when the slope exceeds the incidence angle. Shadowing of the opposite slope appears when α r > 90 o − θ i .
In applications related to land monitoring, an accurate backscatter measurement has a central role and allows robust land cover classification. Therefore, radiometric slope correction is needed in order to reduce these topographic effects on backscattering values and to provide imagery in which pixel values are properly related to the radar backscatter of the scene. In literature, there are different approaches aiming at reducing radiometric distortion.
In this work two physical models have been taken into account. These models propose an exact solution for the compensation of slope-induced variations in the backscattered energy. [33] considers the effects of forested reliefs on the radar backscatter, as an opaque volume composed of isotropic scatterer elements (Eq. 2), whereas [34] derives an equation for the radiometric correction, projecting the 3D model of hillslope without vegetation into the 2D domain of the SAR images and thus considering it as a surface of isotropic scatterers (Eq. 3):
γ f 0 = γ 0 tan ( Π / 2 − θ i ) tan ( Π / 2 − θ i + α r ) ,
γ f 0 = γ 0 cos ( α a z ) cos ( Π / 2 − θ i + α r ) cos ( Π / 2 − θ i + α r ) ,
where γ f 0 and γ 0 are respectively the backscatter on flat terrain and the backscatter on tilted terrain, α a z is the slope in the azimuth direction.

2.3. Denoising

The goal of this framework step is to reduce the intrinsic noise of Sentinel 1 SAR images, a granular pattern distribution called speckle that affects the SAR images. This effect is due to the sum of constructive and destructive superpositions of the backscattered signal after the interaction with the target area. In general, the effort of all despeckling methods is to reduce the speckle noise without losing fine details and edges of features. Among the approaches used for SAR images despeckling, Bayesian methods [35,36,37,38,39], non-Bayesian algorithms [40,41,42], hybrid approaches, and also new methodologies based on Machine Learning algorithms can be mentioned. Comprehensive recent reviews of these methodologies can be found in [43,44,45].
In this paper the non-Bayesian model proposed by Perona & Malik (1990) [40] was used, which is based on the Gaussian kernel convolution and maintains an accurate location of feature edges during the process of image smoothing and restoration, through the definition of a scale-space as follows:
I t = Δ c ( x , y , t ) ∇ I I ( t = 0 ) = I 0
where I t = ∂ I / ∂ t is the partial time derivative of the intensity image, I 0 is the initial intensity image, c ( x , y , t ) is the diffusion coefficient, Δ and ∇ are divergence and gradient operators, respectively.
As noticed by [46] and [47], Gaussian kernel-based methods are equivalent to the solution of the diffusion equation (Eq. 4) which, neglecting the hierarchy of the image levels, reduce both image noise and the definition of object boundaries. With the aim of overcoming these limitations, [40] defined the diffusion coefficient as a function of the gradient magnitude of the image c = g ( ∥ ∇ I ∥ ) . This function, called edge stopping function, ensures a higher rate of diffusion within homogeneous regions, and avoids the blurring of the feature boundaries characterized by high values of ∥ ∇ I ∥ .
Three edge stopping functions were tested. The first two (Eq. 5 and Eq. 6) proposed by [40] and the third (Eq. 7) by [48]:
c 1 = e − ( ∥ ∇ I ∥ / K ) 2 ,
c 2 = 1 1 + ( ∥ ∇ I ∥ / K ) 2 ,
c 3 = 1 2 1 − ∥ ∇ I ∥ K 2 2 2 : ∥ ∇ I ∥ ≤ K 2 0 : o t h e r w i s e .
The constant parameter K allows for the adjustment of the noise filter. The c 1 function stops the diffusion starting from small gradient value, whereas c 2 needs a higher gradient value in order to stop diffusion. The c 3 function stops the diffusion at low gradient values, preserving very fine details. So, c 2 privileges wide regions over small ones, c 1 privileges high contrast edges versus lower contrast edges, and c 3 reduces the diffusion even more rapidly than c 1 and stops diffusion where the gradient is very low (Figure 2).
The most appropriate edge-stopping function in our case is c 1 , as it adequately smooths homogeneous regions, while preserving border lines.

2.4. Thresholding approach to river water delineation

Image segmentation is the process by means of which two or more classes or objects are identified in an image. Various techniques are widely used in research fields ranging from medical applications, recognition and tracking of objects, and environmental analysis, including river and waterbodies delineation either from optical, multispectral and radar data. Two groups can be mentioned: traditional methods (e.g., edge detection, clustering, random forest, support vector machine, markov random field, statistical algorithm), and segmentation processes based on the latest Deep Learning (DL) methods (ANN, CNN and others) [49].
To reduce computational time and implement an efficient automatic procedure, we selected a thresholding method with low consumption of computational resources as the Otsu thresholding algorithm [50], which is simple to implement and has a similar accuracy to more complex methods [51]. The thresholding algorithm, initially implemented by [52], was optimized with the aim of ingesting a stack of images. The algorithm is applied to the grey level histogram of every image and is based on the maximization of the inter-class variance, defined as the weighted sum of variances of the two classes:
σ B 2 ( t ) = σ − σ W 2 ( t ) where :
σ W 2 ( t ) = ω 0 ( t ) · σ 0 2 ( t ) + ω 1 ( t ) · σ 1 2 ( t )
were σ B 2 ( t ) is the inter-class variance, whereas σ W 2 ( t ) is the intra-class variance for the threshold t. The weights ω 0 ( t ) and ω 1 ( t ) are the probabilities of the two classes separated by the threshold t, σ 0 2 ( t ) and σ 1 2 ( t ) are the variances of the two classes.
The thresholding algorithm uses two initial parameters: a first assumption of the value of the VH band (VH 0 ) by means of which approximate wet-dry edges are found ( E 0 ), and the buffer distance from the edges (B d ) defining the area (A h ) in which the histogram is sampled and then used by the Otsu thresholding procedure (Figure 3).
The Canny edge detector [53] implemented into GEE was used for the identification of the approximate wet-dry edges E 0 .
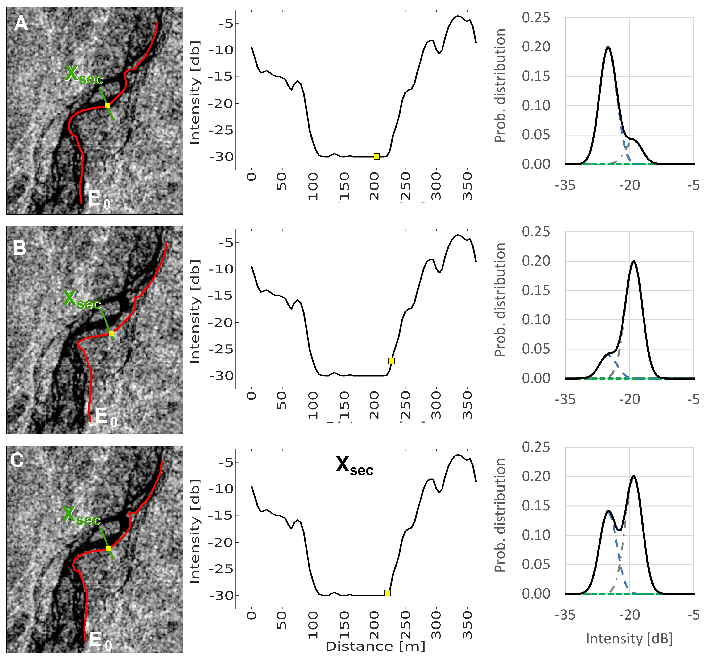
A successful application of the Otsu algorithm depends on the choice of the values of the parameters VH 0 and B d . The initial value of backscattering threshold (VH 0 ) defines the initial classification into water and dry sediment and controls the position of the wet-dry edges E 0 and therefore of the area A h where histograms are sampled. In case of low values of VH 0 , E 0 will be placed in a portions of the image occupied mainly by water with a small proportion of dry sediments.Therefore, A h will be formed mainly by the water class, resulting in a unimodal histogram (Figure 4A). Similarly, if VH 0 is too high, the dry sediment class will dominate A h and the histogram will again be unimodal (Figure 4B). In both cases the Otsu’s thresholding algorithm will fail. Only correct values of VH 0 that identify an area A h composed of approximately 50% of each of the two classes will create a bimodal histogram (Figure 4C).
The choice of buffer amplitude B d is bounded by the channel width. At low discharges the channel width is narrow, whereas it is wider at high discharges. The optimal buffer amplitude is the one that samples half of its area in the channel and the remaining half on dry land, without including other land classes like vegetation or urban areas with higher backscatter values. The influence of the choice of these parameters is reported in Section 4.

3. Case study

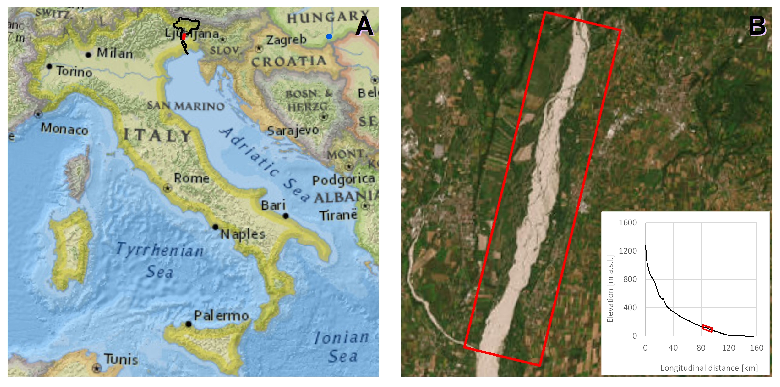
The proposed algorithm has been applied and tested on the Tagliamento river (north east Italy), a large gravel bed braided river recognized as a reference fluvial system for its near-natural dynamics [54]. Its catchment covers an area of about 2700 km 2 from the Italian Alps to the Adriatic Sea, with a total length of 178 km. 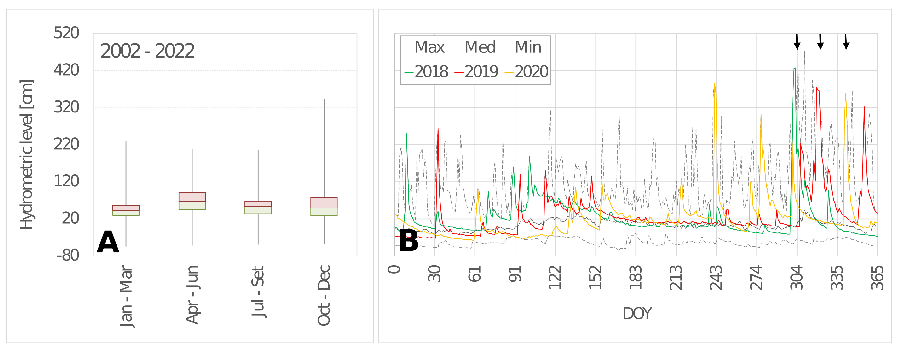The study focuses on a 13 km long reach located in the foothill area of Friulian Pre-Alps, downstream of the Pinzano gorge (Figure 5). It has a mean longitudinal gradient equal to 3.4 m/km and the active channel reaches a width of 1000 m. During flood events this section of the river shows significant variations in the water surface area, induced by the inundation of lateral channels and sediment bars. The reach is also morphologically active, showing frequent erosion of banks and vegetated islands.
The hydrologic regime of the Tagliamento river can be classified as a pluvio-nival regime [54]. The snow melt during the spring season (April - June) sustains the discharge (Figure 6A) ensuring a period of significant mobility of the riverbed, particularly when associated with rain events. Major floods occur generally in autumn, when heavy rains are more likely, with humid air masses moving north from the sea. In the present work we used data from the hydrometric station in Venzone, about 20 km upstream of the study reach, with particular focus on the floods occurred on October 2018, November 2019, and December 2020 (black arrows in Figure 6B).
The new Digital Elevation Model (DEM) of Italy presented by [55] was used to implement the radiometric terrain correction. The DEM was generated through Delaunay tessellation of a heterogeneous dataset, coming from different Italian public bodies. Its vertical accuracy was assessed on an independent sets of control points and, in the region of interest, is less than 2 meters, considered sufficient for the study objectives. The spatial resolution is compatible with the 10 m pixel size of Sentinel-1 imagery.
The correction of the radiometric distortions was performed using the volumetric model (Eq. 2), as suggested by [56] and [57] for case studies with predominant agricultural land use.

4. Results

In this section, we start presenting the sensitivity analysis of the thresholding parameters; then, the calibrated procedure is applied to three flood events in October 2018, November 2019 and December 2020, with return interval approximately of 10, 4 and 3 years, respectively. In particular, we quantified i) the area inundated by water as a function of the water level; and ii) the lateral bank erosion rate.

4.1. Sensitivity analysis

300 Sentinel-1 images entirely covering the study reach were analyzed, in the time spans from January 2014 to June 2021. During this period the hydrometric level at the Venzone gauging station ranged from low flow up to 4.27 m, reached during the flood event named Vaia that occurred at the end of October 2018. At low flow, particularly during summer, the river bed is often completely dry, due to a natural down-welling process in the huge alluvial sediment deposit [58]. To avoid issues with a completely dry reach, we selected images with a corresponding water level at Venzone larger than 0.25 m.
For each image, the procedure outlined in Section 2 and Figure 1 was applied, obtaining a classified map of the water surface extension and the estimated value of the threshold t i that better differentiates between water and dry sediments.
The influence of the buffer amplitude B d on the threshold t i was investigated by means of a sensitivity analysis. The 300 values of t i are reported in Figure 7 as probability density functions, which were then interpolated by a non-parametric kernel distribution where the smoothing function is a Gaussian normal distribution with mean equal to t i and bandwidth of 0.25 dB.
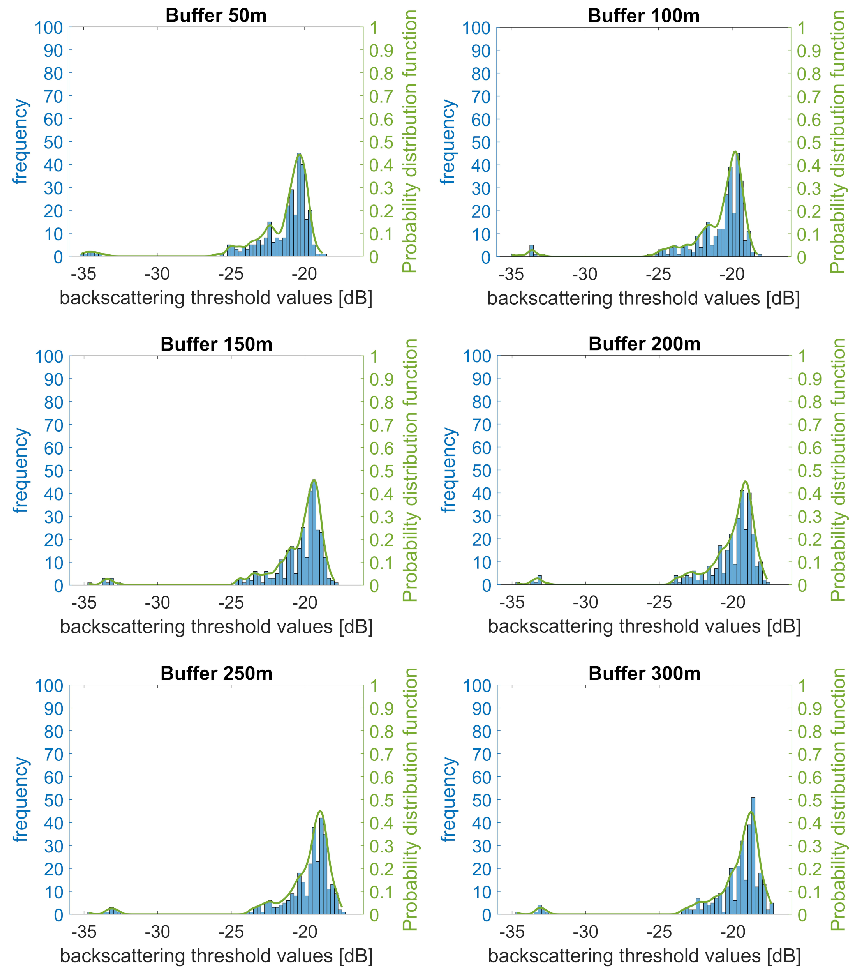
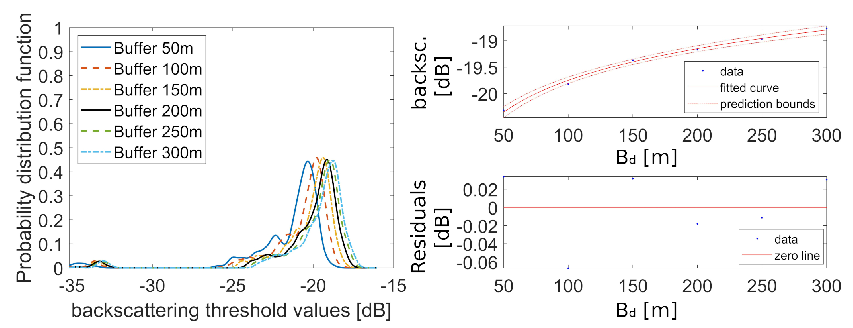
Figure 7 shows the effect of increasing the buffer distance, from 50 m to 300 m. It is worth pointing out that the active corridor width is about 1000 m, with single channels of the braided network 50 m to several hundred meter s wide. It is therefore reasonable to expect a buffer distance in the proposed range. The comparison between the six probability distribution functions and the fitting curve of the most likely threshold values (Figure 8) shows that for increasing values of the buffer amplitude the mode shifts towards positive values. This effect is due to the progressive inclusion of pixels representing other land classes, like vegetation, characterized by volume backscattering, and thus with a stronger backscatter than water and dry sediments. Most probable values of the threshold t i range between -19 and -20 dB, with a maximum mode difference of about 1.5 dB. A higher value of the threshold results in more pixels classified as water. Differences are however limited, in terms of mapping of the main channels. To keep the procedure simple and automated, our suggestion is to select the lower value of the buffer distance, to avoid including a significant number of pixel belonging to other land use classes.
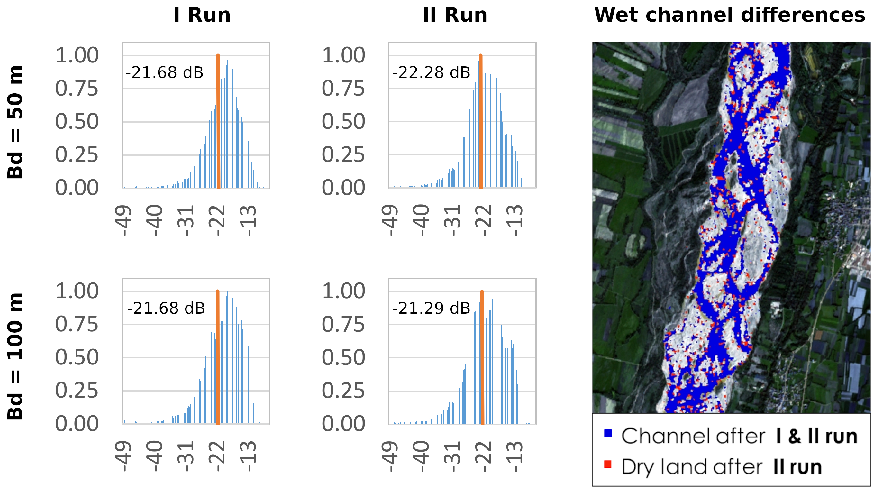
Moreover, the influence of the first value VH 0 was tested, for B d equal to 50 and 100 m, running a second cycle of the thresholding algorithm and imposing the threshold estimate in the first cycle as initial value. Figure 9 shows the histograms of the pixels included in the area A − h with the estimated threshold t i represented by the red vertical line. The second run shows a better separation of the two classes, with a distribution clearly bimodal. However, the values of the threshold are only slightly different, resulting in an estimated area of the water surface that differs mainly because of sparse, isolated pixels (red pixels in the right panel in Figure 9). The histograms in the case of B d equal to 100 m further confirm that with a wider buffer it is likely the area A − h includes a third class of land use (vegetation in this case), represented by the third peak at -14 dB that appears clearly on the right of the histograms after the second run.
Summarizing, the sensitivity analysis suggested us to run the algorithm with a buffer width B d equal to 50 m, and to perform a double cycle, in order to produce histograms with a more pronounced bimodal characteristic and decouple the results from the choice of the first VH 0 value.

4.2. Inundation dynamics

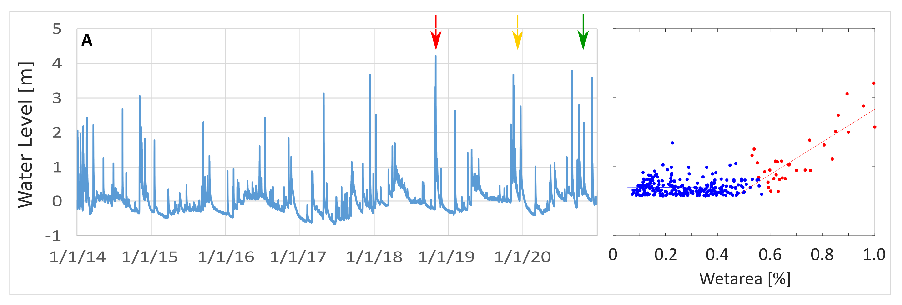
The results of the classification of the water surface area for the 300 images from 2014 to 2021 is shown in Figure 10, in terms of the proportion of total active corridor area inundated by water as a function of the hydrometric level at the Venzone gauging station. Hydrometric data were shifted back by 1 hour with respect to the image timing, to take into account the flood propagation from Venzone to the study reach. The 1 hour shift has been evaluated referring to a second gauging station and approximated hydraulic computations.
Figure 10 shows two distinct behaviors: i) for a water level between 0.25 m and 1 m (red points), the wet area proportion increases markedly from 20% to 60%; ii) for a water level higher than 1 m (blue points) the wet area proportion increases less rapidly, reaching 100%, i.e. full inundation of the active corridor, for a water level of about 3 m. At flow levels lower than 1 m the number of channels increases significantly, with the activation of lateral channels and submergence of low bars. For higher water levels, channels start to merge and the higher bars and vegetated islands are submerged. The values observed from this analysis are similar to what has been observed on shorter reaches by [59,60] who used field surveys and fixed cameras.
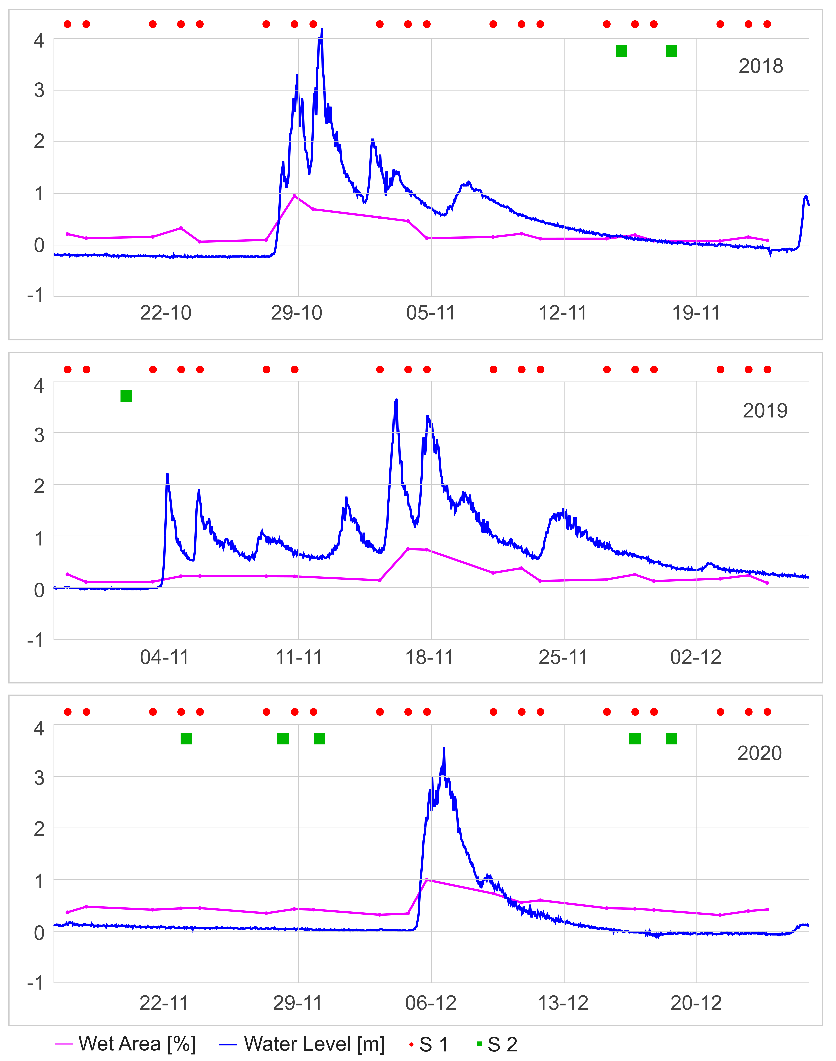
The potentiality of the SAR images mapping is well expressed by the analysis at the single flood scale, for the events in October 2018, November 2019, and December 2020 scale (red, yellow and green arrows in Figure 10A). Figure 11 shows the hydrographs (blue line) registered at the Venzone gauging station and the corresponding time evolution of wet area proportion evaluated at reach scale (magenta line), for the three events. At the top of each panel the red points show the acquisition time of the SAR Sentinel-1 images, whereas green points show the available multi-spectral Sentinel-2 images, highlighting the impossibility to evaluate the during-flood dynamics with this passive sensor.
The analysis shows that in all three events the entire active corridor was inundated (values of the wet area proportion up to 1). Moreover, despite the observed changes in the local configuration of the channel network, the analysis shows little variations in the wet area proportion before and after the flood, indicating a sort of equilibrium at the reach scale. The large variability of the blue points in Figure 10B shows anyway that, particularly at low flow, the channel network configuration may change not only in terms of the location of the channel, but also in terms of the total wet area.
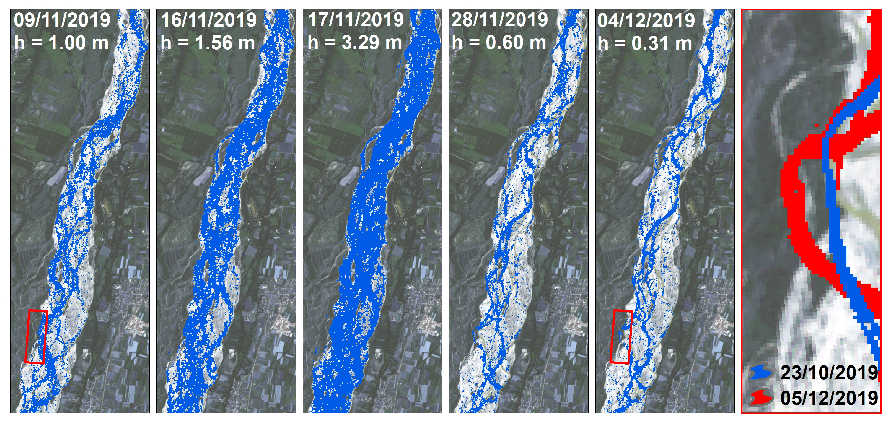
Figure 12 reports with more details the inundation dynamics observed during the event in 2019. November 2019 was a very rainy month, with high flows occurring during the entire month, and 5 subsequent peaks, the highest reaching more than 3.5 m. The first five panels show 5 of the 14 classified SAR images for this month, with water level ranging from 0.31 m to 3.29 m. The images help visualizing the increase in the wet area for higher values of the flow level. Moreover, the classified maps show the changes of the channel network before and after the flood, with several channels formed / closed at high flow. The red box in the bottom-left part of the reach highlights a local example of lateral bank erosion. To better observe the morphological changes a zoom on the red box is reported in the right panel of Figure 12, whit the channel location before the flood mapped in blue and the channel after the flood in red. Bank erosion occurred along 340 m, with an average retreat of about 130 m.
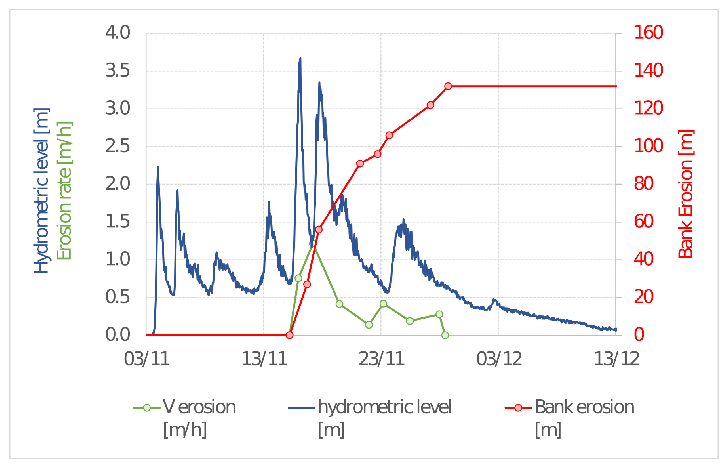
The high temporal resolution of the Sentinel-1 images allows a detailed investigation of the processes of bank erosion. In Figure 13 the time evolution of the cumulative bank erosion (in red) and the erosion velocity (in green) are reported, compared to the flow level (in blue). The analysis shows no erosion during the first 3 smaller floods, with the bank retreat starting during the major peak. In this phase, the bank was eroded with a rate larger than 1 m/h. The erosion continued for several days, with a rate of tens of cm per hour, even if the flow level decreased to values lower than those of the first three floods. These observations support previous studies, pointing out the role of major floods and bank saturation for bank erosion initiation [61].

5. Discussion and conclusions

5.1. Advantages and Limitations of the Proposed Procedure

In this paper was presented an unsupervised and cloud based algorithm, developed within the Python API of Google Earth Engine, which allows the processing of a Sentinel-1 image stack for the automatic detection of river flood dynamics and the associated morphological evolution. As recently pointed out by [62], GEE is a computing platform that can help geomorphologists (and other scientists) using huge amounts of spatially and temporally rich data (in the order of petabytes), overcoming the limitations caused by computing and data storage costs. Remote sensing data significantly transformed fluvial geomorphology in the last decade [10], with most applications involving multi-spectral passive aerial or satellite imagery [63]. Active SAR satellite data such as Sentinel-1 imagery has been demonstrated to provide a valuable asset to map inundated areas [28,64,65], with high accuracy of the water mapping when compared to other sources.
Our investigation confirms the potentiality of this technique and shows that an unsupervised, cloud-based algorithm produces accurate results, with limited need of parameter calibration. In particular, the analysis pointed out the effect of the buffer distance from the estimated edges B d and of the starting value of the backscattering threshold VH 0 needed to compute the initial wet-dry edges. We showed that a relatively small buffer width (compared to the channel width) seems more appropriate to avoid including other land classes in the area of interest where the histograms will be produced. In this way, the selected Otsu thresholding algorithm [50] is most efficient. The sensitivity analysis highlights also that a second cycle, with the computed threshold as starting point may increase the accuracy of the model, producing a more clearly bimodal histograms. However, differences are not large and a cost/benefit analysis depends on the objectives of the study.
Moreover, the proposed procedure is designed to enrich the imagery metadata through flow levels at the time of image acquisition. This allows an automatic selection of the images, based on the flow conditions of interest for the study. Wherever such flow data are available, the GEE procedure automatically extract images above (or below) a defined threshold, significantly reducing the computation time and the operator intervention.
Currently, the processing chain implemented for VH band of Sentinel-1 data requires a limited computational effort to process the images of a flood event (15 - 20 images), in the order of just a few minutes.
The planimetric output for the flooded areas exhibits jaggedness as a result of speckling in SAR data caused by both existing vegetation and water motion, which creates a rippling effect on the water surface. Despite the application of denoising operations, the inherent variability of the backscatter signal has made it challenging to achieve continuous classification, thereby posing a challenge for future development of the methodology.

5.2. Potentiality for fluvial geomorphology

The framework was tested on a 13 km long river section of the Tagliamento River, a large and dynamic gravel bed river, where significant changes of the channel network occur frequently. This gave us the opportunity to test the advantages of SAR data to investigate river dynamics at the sub-flood temporal scale. Indeed, SAR imagery is not affected by cloud cover and this is a foremost advantage when considering flood dynamics. Figure 11 shows the significant difference of usable images considering Sentinel-1 and Sentinel-2 missions, with the latter negatively affected by clouds. Multi-spectral Sentinel-2 imagery provides only before-after flood mapping, rarely allowing for a detailed monitoring during floods.
The application was successful in computing the relationship between wet area proportion and flow level, using 300 images over a period of 7 years. Similar analysis on closeby reaches made in the past [59,60] involved time-consuming field measurements and the installation of fixed cameras, to overcome the lack of remotely-sensed imagery at high flow. The possibility to easily extend this application to other reaches on the same river and in other catchments, opens new perspectives for river managers, assessing differences caused by human intervention and or natural processes, as well as temporal evolution of the morphology.
Furthermore, the proposed mapping procedure proved valid in quantifying river bank erosion rates at the scale of single floods. Bank erosion is a relevant morphological process that affects river evolution and ecology [66]. Predicting and modeling river bank erosion is a challenging task, because it strongly depends on local effects as well as a combination of hydraulic and geotechnical processes of the river and the bank itself, including the root reinforcement in presence of riparian vegetation. To improve our ability to model this process, more observations and quantitative data are essential. Recently, [67] proposed a global inventory of riverbank erosion, based on Landsat imagery of the last 20 years, confirm channel width as the main control, but also highlighting large variability among rivers.
Our application showed that SAR data can be successfully used to quantify riverbank erosion at the event scale, producing valuable information on the erosion rate at daily scale, compared to the monthly/yearly scale of previous remote sensing applications. This allowed for an accurate evaluation of when the bank erosion process started, as well as the relationship with the flow level and its variations in time.
The ground resolution of Sentinel-1 images limits the application to rivers larger than a few hundred meters, to avoid the presence of channels smaller than the pixel size. Higher ground resolution satellites already exist (e.g., COSMO SkyMed and ICEYE) although not easily available as Sentinel-1. However, the fast-evolving number and technology of satellites will soon provide freely accessible imagery at meter or sub-meter resolution, opening the possibility to integrate multi-mission data and achieve sub-daily monitoring of river dynamics during flood events.

References

  1. Anderson, E.P.; Jackson, S.; Tharme, R.E.; Douglas, M.; Flotemersch, J.E.; Zwarteveen, M.; Lokgariwar, C.; Montoya, M.; Wali, A.; Tipa, G.T.; Jardine, T.D.; Olden, J.D.; Cheng, L.; Conallin, J.; Cosens, B.; Dickens, C.; Garrick, D.; Groenfeldt, D.; Kabogo, J.; Roux, D.J.; Ruhi, A.; Arthington, A.H. Understanding rivers and their social relations: A critical step to advance environmental water management. WIREs Water 2019, 6, 1–21. [CrossRef]
  2. Petsch, D.K.; Cionek, V.d.M.; Thomaz, S.M.; dos Santos, N.C.L. Ecosystem services provided by river-floodplain ecosystems. Hydrobiologia 2022. [CrossRef]
  3. Tockner, K.; Stanford, J.A. Riverine flood plains: present state and future trends. Environmental Conservation 2002, 29, 308–330. [CrossRef]
  4. Fryiers, K.A.; Brierley, G.J. In Geomorphic Analysis of River Systems; John Wiley and Sons, Ltd, 2012; pp. 1–345. [CrossRef]
  5. Corenblit, D.; Tabacchi, E.; Steiger, J.; Gurnell, A.M. Reciprocal interactions and adjustments between fluvial landforms and vegetation dynamics in river corridors: A review of complementary approaches. Earth-Science Reviews 2007, 84, 56–86. [CrossRef]
  6. Phillips, J.D. Evolutionary geomorphology: thresholds and nonlinearity in landform response to environmental change. Hydrology and Earth System Sciences 2006, 10, 731–742. [CrossRef]
  7. Fryirs, K.A. River sensitivity: a lost foundation concept in fluvial geomorphology. Earth Surface Processes and Landforms 2017, 42, 55–70. [CrossRef]
  8. European Commission. Water Framework Directive, 2000. https://eur-lex.europa.eu/eli/dir/2000/60/oj.
  9. European Commission. Flood Directive, 2007. https://eur-lex.europa.eu/eli/dir/2007/60/oj.
  10. Piégay, H.; Arnaud, F.; Belletti, B.; Bertrand, M.; Bizzi, S.; Carbonneau, P.; Dufour, S.; Liébault, F.; Ruiz-Villanueva, V.; Slater, L. Remotely sensed rivers in the Anthropocene: state of the art and prospects. Earth Surface Processes and Landforms 2020, 45, 157–188. [CrossRef]
  11. Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [CrossRef]
  12. Gomes, V.C.F.; Queiroz, G.R.; Ferreira, K.R. An Overview of Platforms for Big Earth Observation Data Management and Analysis. Remote Sensing 2020, 12. [CrossRef]
  13. Smith, L. Satellite remote sensing of river inundation area, stage, and discharge: A review. Hydrological Processes 1997, 11, 1427–1439. [CrossRef]
  14. Pavelsky, T.M.; Smith, L.C. RivWidth: A Software Tool for the Calculation of River Widths From Remotely Sensed Imagery. IEEE Geoscience and Remote Sensing Letters 2008, 5, 70–73. [CrossRef]
  15. Monegaglia, F.; Zolezzi, G.; Güneralp, I.; Henshaw, A.J.; Tubino, M. Automated extraction of meandering river morphodynamics from multitemporal remotely sensed data. Environmental Modelling and Software 2018, 105, 171–186. [CrossRef]
  16. Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–4220. [CrossRef]
  17. Isikdogan, F.; Bovik, A.; Passalacqua, P. RivaMap: An automated river analysis and mapping engine. Remote Sensing of Environment 2017, 202, 88–97. [CrossRef]
  18. Spada, D.; Molinari, P.; Bertoldi, W.; Vitti, A.; Zolezzi, G. Multi-Temporal Image Analysis for Fluvial Morphological Characterization with Application to Albanian Rivers. ISPRS International Journal of Geo-Information 2018, 7. [CrossRef]
  19. Brakenridge, G.R.; Knox, J.C.; Paylor, E.D.; Magilligan, F.J. Radar remote sensing aids study of the Great Flood of 1993. Eos, Transactions American Geophysical Union 1994, 75, 521–527. [CrossRef]
  20. Dellepiane, S.; Angiati, E.; Vernazza, G. Processing and segmentation of COSMO-SkyMed images for flood monitoring. 2010 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2010, pp. 4807–4810. [CrossRef]
  21. Pulvirenti, L.; Chini, M.; Pierdicca, N.; Guerriero, L.; Ferrazzoli, P. Flood monitoring using multi-temporal COSMO-SkyMed data: Image segmentation and signature interpretation. Remote Sensing of Environment 2011, 115, 990–1002. [CrossRef]
  22. Amitrano, D.; Di Martino, G.; Iodice, A.; Riccio, D.; Ruello, G. Unsupervised Rapid Flood Mapping Using Sentinel-1 GRD SAR Images. IEEE Transactions on Geoscience and Remote Sensing 2018, 56, 3290–3299. [CrossRef]
  23. Moharrami, M.; Javanbakht, M.H.; Attarchi, S. Automatic flood detection using sentinel-1 images on the google earth engine. Environmental Monitoring and Assessment 2021, 193. [CrossRef]
  24. Zhou, S.; Kan, P.; Silbernagel, J.; Jin, J. Application of Image Segmentation in Surface Water Extraction of Freshwater Lakes using Radar Data. ISPRS International Journal of Geo-Information 2020, 9. [CrossRef]
  25. Amitrano, D.; Di Martino, G.; Iodice, A.; Riccio, D.; Ruello, G. A New Framework for SAR Multitemporal Data RGB Representation: Rationale and Products. IEEE Transactions on Geoscience and Remote Sensing 2015, 53, 117–133. [CrossRef]
  26. Papa, M.N.; Ruello, G.; Mitidieri, F.; Amitrano, D. Advanced Technologies for Satellite Monitoring of Water Resources. Frontiers in Water-Energy-Nexus—Nature-Based Solutions, Advanced Technologies and Best Practices for Environmental Sustainability; Naddeo, V.; Balakrishnan, M.; Choo, K.H., Eds.; Springer International Publishing: Cham, 2020; pp. 157–160. [CrossRef]
  27. Klemenjak, S.; Waske, B.; Valero, S.; Chanussot, J. Automatic Detection of Rivers in High-Resolution SAR Data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2012, 5, 1364–1372. [CrossRef]
  28. Obida, C.B.; Blackburn, G.A.; Whyatt, J.D.; Semple, K.T. River network delineation from Sentinel-1 SAR data. International Journal of Applied Earth Observation and Geoinformation 2019, 83. [CrossRef]
  29. Nykanen, D.; Foufoula-Georgiou, E.; Sapozhnikov, V. Study of spatial scaling in braided river patterns using synthetic aperture radar imagery. Water Resources Research 1998, 34, 1795–1808. [CrossRef]
  30. Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sensing of Environment 2017, 202, 18–27. [CrossRef]
  31. Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: a fully automated processing chain. International Journal of Remote Sensing 2016, 37, 2990–3004. [CrossRef]
  32. Jong-Sen Lee, E.P., Ed. Polarimetric Radar Imaging; CRC Press, 2009. [CrossRef]
  33. Hoekman, D.H. Radar remote sensing data for applications in forestry; Wageningen University and Research, 1990.
  34. Ulander, L.M.H. Radiometric slope correction of synthetic-aperture radar images. IEEE Transactions on Geoscience and Remote Sensing 1996, 34, 1115–1122. [CrossRef]
  35. Lee, J.S. Digital Image Enhancement and Noise Filtering by Use of Local Statistics. IEEE Transactions on Pattern Analysis and Machine Intelligence 1980, PAMI-2, 165–168. [CrossRef]
  36. Lee, J.S. Refined filtering of image noise using local statistics. Computer Graphics and Image Processing 1981, 15, 380–389. [CrossRef]
  37. Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise. IEEE Transactions on Pattern Analysis and Machine Intelligence 1982, PAMI-4, 157–166. [CrossRef]
  38. Lopes, A.; Nezry, E.; Touzi, R.; Laur, H. Maximum A Posteriori Speckle Filtering And First Order Texture Models In Sar Images. 10th Annual International Symposium on Geoscience and Remote Sensing. IEEE, 1990, pp. 2409–2412. [CrossRef]
  39. Baraldi, A.; Parmiggiani, F. A refined gamma MAP SAR speckle filter with improved geometrical adaptivity. IEEE Transactions on Geoscience and Remote Sensing 1995, 33, 1245–1257. [CrossRef]
  40. Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence 1990, 12, 629–639. [CrossRef]
  41. Lee, J.S. Digital image smoothing and the sigma filter. Comput. Vis. Graph. Image Process. 1983, 24, 255–269.
  42. Lee, J.S.; Wen, J.H.; Ainsworth, T.L.; Chen, K.S.; Chen, A.J. Improved Sigma Filter for Speckle Filtering of SAR Imagery. IEEE Transactions on Geoscience and Remote Sensing 2009, 47, 202–213. [CrossRef]
  43. Argenti, F.; Lapini, A.; Bianchi, T.; Alparone, L. A Tutorial on Speckle Reduction in Synthetic Aperture Radar Images. IEEE Geoscience and Remote Sensing Magazine 2013, 1, 6–35. [CrossRef]
  44. Singh, P.; Diwakar, M.; Shankar, A.; Pandey, R.S.; Kumar, M. A Review on SAR Image and its Despeckling. Archives of Computational Methods in Engineering 2021, 28, 4634–4653. [CrossRef]
  45. Baraha, S.; Sahoo, A.K.; Modalavalasa, S. A systematic review on recent developments in nonlocal and variational methods for SAR image despeckling. Signal Processing 2022, 196, 108521. [CrossRef]
  46. Hummel, R.; Moniot, R. Reconstructions from zero crossings in scale space. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37, 2111–2130. [CrossRef]
  47. Koenderink, J. The structure of images. Biological Cybernetics 1984, 50, 363–370. [CrossRef]
  48. Black, M.; Sapiro, G.; Marimont, D.; Heeger, D. Robust anisotropic diffusion. IEEE Transactions on Image Processing 1998, 7, 421–432. [CrossRef]
  49. Guo, Z.; Wu, L.; Huang, Y.; Guo, Z.; Zhao, J.; Li, N. Water-Body Segmentation for SAR Images: Past, Current, and Future. Remote Sensing 2022, 14. [CrossRef]
  50. Otsu, N. A threshold selection method from gray level histograms. IEEE Transactions on Systems, Man, and Cybernetics 1979, 9, 62–66. [CrossRef]
  51. Kheradmandi, N.; Mehranfar, V. A critical review and comparative study on image segmentation-based techniques for pavement crack detection. Construction and Building Materials 2022, 321, 126162. [CrossRef]
  52. Donchyts, G.; Schellekens, J.; Winsemius, H.; Eisemann, E.; Van de Giesen, N. A 30 m Resolution Surface Water Mask Including Estimation of Positional and Thematic Differences Using Landsat 8, SRTM and OpenStreetMap: A Case Study in the Murray-Darling Basin, Australia. Remote Sensing 2016, 8. [CrossRef]
  53. Canny, J. A Computational Approach to Edge Detection. IEEE Transactions on Pattern Analysis and Machine Intelligence 1986, PAMI-8, 679–698. [CrossRef]
  54. Tockner, K.; Ward, J.V.; Arscott, D.B.; Edwards, P.J.; Kollmann, J.; Gurnell, A.M.; Petts, G.E.; Maiolini, B. The Tagliamento River: a model ecosystem of European importance. Aquatic Sciences 2003, 65, 239–253. [CrossRef]
  55. Tarquini, S.; Isola, I.; Favalli, M.; Mazzarini, F.; Bisson, M.; Pareschi, M.; Boschi, E. TINITALY/01: a new triangular irregular network of Italy. Annals of Geophysics 2007, 50. [CrossRef]
  56. Hoekman, D.; Reiche, J. Multi-model radiometric slope correction of SAR images of complex terrain using a two-stage semi-empirical approach. Remote Sensing of Environment 2015, 156, 1–10. [CrossRef]
  57. Vollrath, A.; Mullissa, A.; Reiche, J. Angular-Based Radiometric Slope Correction for Sentinel-1 on Google Earth Engine. Remote Sensing 2020, 12. [CrossRef]
  58. Doering, M.; Uehlinger, U.; Rotach, A.; Schlaepfer, D.R.; Tockner, K. Ecosystem expansion and contraction dynamics along a large Alpine alluvial corridor (Tagliamento River, Northeast Italy). Earth Surface Processes and Landforms 2007, 32, 1693–1704. [CrossRef]
  59. van der Nat, D.; Schmidt, A.P.; Tockner, K.; Edwards, P.J.; Ward, J.V. Inundation Dynamics in Braided Floodplains: Tagliamento River, Northeast Italy. Ecosystems 2002, 5, 636–647. [CrossRef]
  60. Welber, M.; Bertoldi, W.; Tubino, M. The response of braided planform configuration to flow variations, bed reworking and vegetation: The case of the Tagliamento River, Italy. Earth Surface Processes and Landforms 2012, 37, 572–582. [CrossRef]
  61. Rinaldi, M.; Darby, S.E. 9 Modelling river-bank-erosion processes and mass failure mechanisms: progress towards fully coupled simulations. In Gravel-Bed Rivers VI: From Process Understanding to River Restoration; Elsevier, 2007; Vol. 11, Developments in Earth Surface Processes, pp. 213–239. [CrossRef]
  62. Boothroyd, R.J.; Williams, R.D.; Hoey, T.B.; Barrett, B.; Prasojo, O.A. Applications of Google Earth Engine in fluvial geomorphology for detecting river channel change. WIREs Water 2021, 8, e21496. [CrossRef]
  63. Bizzi, S.; Demarchi, L.; Grabowski, R.; Weissteiner, C.J.; Van de Bund, W. The use of remote sensing to characterise hydromorphological properties of European rivers. Aquatic Sciences 2016, 78, 57–70. [CrossRef]
  64. Clement, M.; Kilsby, C.; Moore, P. Multi-temporal synthetic aperture radar flood mapping using change detection. Journal of Flood Risk Management 2018, 11, 152–168. [CrossRef]
  65. Wu, X.; Zhang, Z.; Xiong, S.; Zhang, W.; Tang, J.; Li, Z.; An, B.; Li, R. A Near-Real-Time Flood Detection Method Based on Deep Learning and SAR Images. Remote Sensing 2023, 15. [CrossRef]
  66. Florsheim, J.L.; Mount, J.F.; Chin, A. Bank Erosion as a Desirable Attribute of Rivers. BioScience 2008, 58, 519–529. [CrossRef]
  67. Langhorst, T.; Pavelsky, T. Global Observations of Riverbank Erosion and Accretion From Landsat Imagery. Journal of Geophysical Research: Earth Surface 2023, 128, e2022JF006774. [CrossRef]
Preprints 75817 g001
Figure 1. Diagram of the proposed framework (left) and GEE architecture (right) [30] for mapping the channel area from Sentinel-1 imagery.
Figure 1. Diagram of the proposed framework (left) and GEE architecture (right) [30] for mapping the channel area from Sentinel-1 imagery.
Preprints 75817 g001
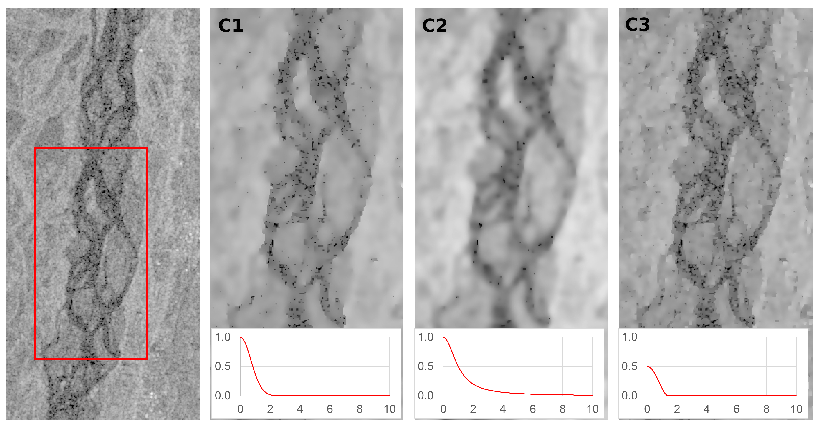
Preprints 75817 g002
Figure 2. An example of the different denoising functions on Sentinel-1 imagery. From left to right: original VH band; denoised images using equations 5, 6, and 7, respectively. The three denoising functions are also plotted in the bottom sub-panels as a function of ∥ ∇ I ∥ .
Figure 2. An example of the different denoising functions on Sentinel-1 imagery. From left to right: original VH band; denoised images using equations 5, 6, and 7, respectively. The three denoising functions are also plotted in the bottom sub-panels as a function of ∥ ∇ I ∥ .
Preprints 75817 g002
Preprints 75817 g003
Figure 3. An example of the thresholding algorithm. From left to right: definition of the initial wet-dry edges E 0 and of the area A h (as a buffer with a distance B d ) in which the Otsu algorithm is then applied.
Figure 3. An example of the thresholding algorithm. From left to right: definition of the initial wet-dry edges E 0 and of the area A h (as a buffer with a distance B d ) in which the Otsu algorithm is then applied.
Preprints 75817 g003
Preprints 75817 g004
Figure 4. Three examples of the effect of on the wet-dry edges E 0 for different values of VH 0 , namely a low value (row A) a high value (row B) and a correct value (row C). For each example, the left panel shows the SAR image with the initial wet-dry edges (red line) and the cross section (green line) reported in the central panel. On the right, the histogram of the SAR backscatter intensity.
Figure 4. Three examples of the effect of on the wet-dry edges E 0 for different values of VH 0 , namely a low value (row A) a high value (row B) and a correct value (row C). For each example, the left panel shows the SAR image with the initial wet-dry edges (red line) and the cross section (green line) reported in the central panel. On the right, the histogram of the SAR backscatter intensity.
Preprints 75817 g004
Preprints 75817 g005
Figure 5. Location of the Tagliamento catchment in north east Italy (left) and aerial view of the study site (right). The inset panel shows the longitudinal bed profile of the river, with the investigated reach highlighted in red.
Figure 5. Location of the Tagliamento catchment in north east Italy (left) and aerial view of the study site (right). The inset panel shows the longitudinal bed profile of the river, with the investigated reach highlighted in red.
Preprints 75817 g005
Preprints 75817 g006
Figure 6. A) seasonal flow variation from 2002 to 2022, and B) flow regime for the years 2018, 2019 and 2020, as measured at the Venzone gouging station. In panel B) the gray solid line and the two gray dashed lines are the median, the maximum, and the minimum value for every single day in the period 2002 - 2022, respectively.
Figure 6. A) seasonal flow variation from 2002 to 2022, and B) flow regime for the years 2018, 2019 and 2020, as measured at the Venzone gouging station. In panel B) the gray solid line and the two gray dashed lines are the median, the maximum, and the minimum value for every single day in the period 2002 - 2022, respectively.
Preprints 75817 g006
Preprints 75817 g007
Figure 7. Probability density functions of the estimated threshold t i between wet and dry areas, for the six increasing values of the buffer amplitude B d .
Figure 7. Probability density functions of the estimated threshold t i between wet and dry areas, for the six increasing values of the buffer amplitude B d .
Preprints 75817 g007
Preprints 75817 g008
Figure 8. Comparison of the interpolated probability density functions obtained in the six cases with B d varying from 50 to 300 meter (left); and fitting of the most likely threshold values with prediction bounds and residuals (right).
Figure 8. Comparison of the interpolated probability density functions obtained in the six cases with B d varying from 50 to 300 meter (left); and fitting of the most likely threshold values with prediction bounds and residuals (right).
Preprints 75817 g008
Preprints 75817 g009
Figure 9. Comparison of the histograms and related threshold values between first and second cycle (left and middle panels, respectively) in the cases of buffer width B d equal to 50 and 100 m (first and second row, respectively). The right panel shows the differences in the classified water surface area in the case of B d equal to 50 m.
Figure 9. Comparison of the histograms and related threshold values between first and second cycle (left and middle panels, respectively) in the cases of buffer width B d equal to 50 and 100 m (first and second row, respectively). The right panel shows the differences in the classified water surface area in the case of B d equal to 50 m.
Preprints 75817 g009
Preprints 75817 g010
Figure 10. A) Water level recorded at the gauging station of Venzone from 2014 to 2021; B) wet area proportion for the 300 analyzed images.
Figure 10. A) Water level recorded at the gauging station of Venzone from 2014 to 2021; B) wet area proportion for the 300 analyzed images.
Preprints 75817 g010
Preprints 75817 g011
Figure 11. Temporal evolution of water level (blue line) and the corresponding wet area proportion (magenta line) for the three floods of October 2018, November 2019, and December 2020 (top to bottom panels, respectively). Red dots are the available Sentinel-1 images and the green dots are the Sentinel-2 available images with cloud cover less than 15%.
Figure 11. Temporal evolution of water level (blue line) and the corresponding wet area proportion (magenta line) for the three floods of October 2018, November 2019, and December 2020 (top to bottom panels, respectively). Red dots are the available Sentinel-1 images and the green dots are the Sentinel-2 available images with cloud cover less than 15%.
Preprints 75817 g011
Preprints 75817 g012
Figure 12. Maps of the estimated wet area during the floods in November 2019, for different values of the water level. The red box in the bottom left locates a major lateral bank erosion event highlighted in the last panel on the right.
Figure 12. Maps of the estimated wet area during the floods in November 2019, for different values of the water level. The red box in the bottom left locates a major lateral bank erosion event highlighted in the last panel on the right.
Preprints 75817 g012
Preprints 75817 g013
Figure 13. Time evolution of the cumulative lateral erosion (red line) and erosion rate (green line), compared to the flow level measured at the Venzone gauging station (blue line).
Figure 13. Time evolution of the cumulative lateral erosion (red line) and erosion rate (green line), compared to the flow level measured at the Venzone gauging station (blue line).
Preprints 75817 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated