Memoryless Property of the Income Distribution as an Indication for Testing the Equality of Opportunity: Evidence from China (1978-2015)

Preprint

Article

Memoryless Property of the Income Distribution as an Indication for Testing the Equality of Opportunity: Evidence from China (1978-2015)

Altmetrics

Downloads

138

Views

Comments

Yong Tao^*

This version is not peer-reviewed

Submitted:

14 March 2023

Posted:

15 March 2023

You are already at the latest version

Alerts

Abstract

It has been well known that the exponential distribution is the only continuous distribution that has the memoryless property. Here, we observe that, if the exponential distribution dominates an economy as a probability distribution of income acquisition, then the memoryless property imposes equal opportunities on agents in this economy to acquire earnings. Based on this observation, we propose to identify the emergence of an exponential income distribution as a potential necessary condition for guaranteeing the equality of opportunity. Together with other conditions (such as social and economic mobility), it would promote equal opportunities for income acquisition among citizens. Empirically, we employ the latest data available from four representative market-economy countries (the United Kingdom, the United States, Canada, and China) to demonstrate that the exponential distribution is a stylized feature of the income structure of the low- and middle-income class, which occupies the great majority of populations. By contrast, the top income classes in these countries obey the Pareto distribution. To validate the relationship between exponential distribution and equal opportunity, we empirically show how the income structure of the low- and middle-income class in China (from 1978 to 2015) evolved towards an exponential distribution after the market-oriented economic reformation.

Keywords:

Subject: Business, Economics and Management - Economics

1. Introduction

Nowadays, it has been known that the Matthew effect in income allocations leads to the Pareto distribution of income (Champernowne, 1953; Wold and Whittle, 1957; Angle, 1993; Lux and Marchesi, 1999; Saichev et al., 2009; Benhabib et al., 2011; Malevergne et al., 2013). At the end of the 19th century, the economist Pareto (1897) first found that the rich part of populations in several European countries for the 15th-19th centuries obeyed a Pareto distribution. This finding was later supported by substantial empirical evidence (Mandelbrot, 1960; Aoyama et al., 2000; Atkinson et al., 2011; Aoki and Nirei, 2017; Jones and Kim, 2018; Tao et al., 2019). Today, the Pareto distribution has been observed universally in the richest class (1%~3% of populations); however, this distribution could apply to a larger proportion of populations when going further back in history to Renaissance Europe (Souma, 2002), Hungarian medieval society (Hegyi et al., 2007), and ancient Egypt (Abul-Magd, 2002). For example, there had been evidence showing that the wealth structure of an ancient Egypt city in the 14th century BC followed a Pareto distribution (Abul-Magd, 2002).

As the time came to the end of the 20th century, it had been found that the income structure of market-economy countries around the world uniformly exhibited a two-class pattern (Dragulescu and Yakovenko, 2001; Nirei and Souma, 2007; Newby et al., 2011; Prinz, 2016; Shaikh, 2017; Irwin and Irwin, 2017; Rosser, 2019; Tao et al., 2019; Ma and Ruzic, 2020; Lim and Min, 2020): the great majority of populations obeyed an exponential distribution and the remaining (richest) part followed a Pareto distribution. Empirical evidence had covered more than 66 countries (Tao et al., 2019), ranging from Europe to Latin America, North America, and Asia. In the economic literature, it has been known that the economic mechanism for generating the Pareto distribution is related to the proportional growth (i.e., Gibrat’s law for income dynamics), which highlights the Matthew effect in income accumulation (Gabaix, 1999; Malevergne et al., 2013; Gabaix et al., 2016; Aoki and Nirei, 2017; Jones and Kim, 2018). However, there is scant understanding of the economic mechanism for driving the exponential income distribution. In the theory of probability, it has been well known that the exponential distribution is the only (continuous) memoryless distribution (Marsaglia and Tubilla, 1975; Shimizu, 1979; Huang, 1981). The memoryless property says that knowledge of what has occurred in the past has no effect on future probabilities. In this paper, we find that the memoryless property has an economic significance in identifying a fair income distribution. In particular, we observe that, if the exponential distribution dominates an economy as a probability distribution of income acquisition, then the memoryless property would impose equal opportunities on agents in this economy to acquire earnings. Based on this finding, we propose to identify the emergence of an exponential income distribution as a potential condition for equalizing opportunities for income acquisition among citizens. Despite this, we need to clarify that the emergence of an exponential income structure does not indicate an exponential probability distribution of income. Conversely, the latter can lead to the former. Therefore, we identify the exponential income distribution as a necessary condition for promoting the equality of opportunity. However, if the exponential income structure is broken, we must deduce that the probability distribution of income has “memories” for certain social members, which would undermine the equality of opportunity in the sense of Rawls (1999). To investigate the economic feasibility of income dynamics for generating an exponential income distribution, we further employ the random growth theory of income distribution (Gabaix, 1999; Gabaix et al., 2016; Aoki and Nirei, 2017; Jones and Kim, 2018) to show that, if all agents in an economy have equal opportunities to acquire any given income, then the resulting income structure of this economy yields an exponential distribution.

The rest of this paper is organized as follows. Section 2 introduces the memoryless property of the exponential distribution, and shows that, if the exponential distribution dominates an economy as a probability distribution of income acquisition, then the memoryless property imposes equal opportunities on agents in this economy to acquire earnings. Section 3 shows that the random growth theory of income distribution can provide an economic description for the income dynamics of generating the exponential distribution and the Pareto distribution. Section 4 empirically shows that the income structure of a market-economy country can be approximately described by a two-class distribution function, where the low- and middle-income class obeys the exponential distribution and the top income class obeys the Pareto distribution. In section 5, we use the random growth theory to provide a possible explanation for why the income structure of a market-economy country is described by a two-class distribution. Section 6 concludes.

2. Memoryless property and exponential income distribution

To explore the potential relationship between exponential income distribution and equal opportunity, it has been theoretically shown that the exponential income distribution can be generated in a peer-to-peer economic network that shares the publicly available technology, which eliminates the opportunity inequality of market competition (Tao, 2016, 2021; Tao et al., 2021). This peer-to-peer economic network is simulated by an idealized Arrow-Debreu economy (Arrow and Debreu, 1954). Because the peer-to-peer economic network is a decentralized market economy that highlights the equal opportunity of competition, Tao (2016, 2021) proposes to identify the equal opportunity of market competition as the underlying economic mechanism for driving the exponential income distribution. However, this proposal still remains open. In this paper, we provide a novel perspective to formalize the relationship between exponential income distribution and equal opportunity. To this end, we first introduce the memoryless property of the exponential distribution.

Let

X

be a non-negative random variable with the distribution

P (X \geq t)

. We say that the distribution

P (X \geq t)

lacks memory at

s

P (X \geq s) > 0

and the following equation (1) is satisfied1 (Marsaglia and Tubilla, 1975; Shimizu, 1979; Huang, 1981).

P (X \geq s + t| X \geq s) = P (X \geq t),

(1)

where

P (X \geq s + t| X \geq s)

denotes the conditional probability of

X \geq s + t

given

X \geq s

In the theory of probability, it has been proved that the exponential distribution is the only continuous distribution to satisfy equation (1) (Marsaglia and Tubilla, 1975; Shimizu, 1979; Huang, 1981). Therefore, let us write

P (X \geq t)

as an exponential distribution2:

P (X \geq t) = e x p (- \frac{t}{θ}),

(2)

where

0 \leq t < + \infty

and

θ > 0

, with

θ

being a parameter.

If we use the exponential distribution (2) to describe the income structure of an economy, then

P (X \geq t)

denotes the fraction of population with the income higher than

t

, where

t

denotes the income level. Here, we further show that, if the exponential distribution (2) dominates the economy as a probability distribution of income acquisition, then the memoryless property (1) imposes equal opportunities on agents in this economy to acquire earnings. To this end, we assume that the income dynamics allow agents to change their income status such that the exponential income distribution (2) can be regarded as a probability distribution of income acquisition. This means that social and economic mobility is allowed for. Without loss of generality, let us consider two agents A and B in this economy who have the incomes

X_{A}

and

X_{B}

, respectively. We further assume that the agent A is a rich person who has savings of 1000000 dollars, while the agent B is a poor person who has savings of 10 dollars. Then, we ask a question: In future, who will more likely win earnings of 10000 dollars given their savings?

Intuitively, it seems that the agent A should win 10000 dollars more likely. However, by the memoryless property (1), the agent A’s probability of winning 10000 dollars is denoted by

P (X_{A} \geq 1010000| X_{A} \geq 1000000) = P (X_{A} \geq 10000),

(3)

while the agent B’s probability of winning 10000 dollars is denoted by

P (X_{B} \geq 10010| X_{B} \geq 10) = P (X_{B} \geq 10000) .

(4)

Equations (3) and (4) indicate:

P (X_{A} \geq 1010000| X_{A} \geq 1000000) = P (X_{B} \geq 10010| X_{B} \geq 10),

(5)

which means that agents A and B have equal opportunities to win 10000 dollars!

In this sense, the memoryless property (1) may promote the emergence of an equal-opportunity economy in which an agent’s future earnings are irrelevant with the agent’s past income accumulation. This property radically distinguishes the exponential income distribution (2) from the Pareto distribution of income, because the latter is driven by the Matthew effect in income accumulation, that is, an agent’s future earnings benefit from the agent’s past income accumulation. To see this, let us write the Pareto distribution as below (Aoki and Nirei, 2017; Jones and Kim, 2018):

F (X \geq t) = {(t / μ_{0})}^{- β},

(6)

where

t \geq μ_{0} > 0

and

β \geq 1

Now, we assume that the probability distribution of income acquisition is denoted by the Pareto law (6). Then, by equation (6), it is easy to work out

F (X \geq s + t| X \geq s) = \frac{F (X \geq s + t \cap X \geq s)}{F (X \geq s)} = \frac{F (X \geq s + t)}{F (X \geq s)} = {(1 + \frac{t}{s})}^{- β},

(7)

which means that an agent’s probability of acquiring future earnings

t

is positively dependent on the agent’s past income accumulation

s

, indicating the Matthew effect in income accumulation. In particular, by equation (7) we have

\lim_{s \to + \infty} F (X \geq s + t| X \geq s) = 1;

(8)

that is, if an agent’s past income accumulation

s

is sufficiently large, then the agent has the potential to win any earnings

t

in the future.

In political philosophy, the “veil of ignorance” is proposed to promote an equal-opportunity society (Rawls, 1999). Because the memoryless property (1) separates the past information from future events, an exponential probability distribution of income might facilitate the emergence of a “veil of ignorance”, in which all agents tend to “forget” the knowledge of past income accumulations. However, we observe that the memoryless property (1) promotes equal opportunities of income acquisition if and only if the income dynamics allow agents to change their income status such that the exponential distribution (2) can be regarded as a probability distribution of income acquisition. From this sense, the exponential income distribution can only serve as a potential necessary condition for equalizing opportunities for income acquisition among citizens. To investigate the economic feasibility of income dynamics for generating an exponential income distribution, we next consider the random growth theory of income distribution in the economic literature (Gabaix, 1999; Gabaix et al., 2016; Aoki and Nirei, 2017; Jones and Kim, 2018).

3. Income dynamics

Let us consider a free-market economy in which agents are heterogeneous in their income. If we denote the income of an agent by

x (τ)

at the time

τ

, then, by the setting of the random growth theory, the agent’s income will obey the Ito process (Gabaix, 1999; Gabaix et al., 2016):

d x = A (x, τ) d τ + B (x, τ) d W (τ),

(9)

where,

W (τ)

denotes the standard Brownian motion, and

A (x, τ)

and

B (x, τ)

are two continuous functions of

x

and

τ

Based on equation (9), by Ito’s Lemma, it has been known that the density of the income distribution

f (x, τ)

satisfies a Kolmogorov forward equation (Gabaix, 1999; Gabaix et al., 2016; Aoki and Nirei, 2017; Jones and Kim, 2018):

\frac{\partial f (x, τ)}{\partial τ} = - δ f (x, τ) - \frac{\partial [A (x, τ) f (x, τ)]}{\partial x} + \frac{1}{2} \frac{\partial^{2} [{B (x, τ)}^{2} f (x, τ)]}{\partial x^{2}},

(10)

where the term

- δ f (x, τ)

denotes the “stabilizing force” with the constant

δ \geq 0

, and it means that agents may retire at rate

δ

(Gabaix et al., 2016).

If a stationary distribution,

\lim_{τ \to \infty} f (x, τ) = f (x)

, exists, then it satisfies

0 = - δ f (x) - \frac{\partial [A (x, τ) f (x)]}{\partial x} + \frac{1}{2} \frac{\partial^{2} [{B (x, τ)}^{2} f (x)]}{\partial x^{2}} .

(11)

To derive the Pareto distribution, one needs to assume (Gabaix, 1999; Malevergne et al., 2013; Gabaix et al., 2016; Jones and Kim, 2018):

A (x, τ) = ω_{0} x

and

B (x, τ) = σ_{0} x

, where

ω_{0}

and

σ_{0}

are two constants. Substitute both of them into equation (9) we have

d x = ω_{0} x d τ + σ_{0} x d W (τ),

(12)

By equation (12), the increment of the expected value of an agent’s income is equal to

d E [x] = ω_{0} E [x] d τ,

(13)

where we have used

E [\int x d W (τ)] = 0

Equation (13) means that the increment of the expected value of an agent’s income depends on the agent’s current (expected) income

E [x]

, indicating the Matthew effect in income accumulation. This equation is well known as Gibrat’s law (Gabaix, 1999; Malevergne et al., 2013; Gabaix et al., 2016; Jones and Kim, 2018). Now, we show that Gibrat’s law for income dynamics leads to the Pareto distribution. To this end, substitute

A (x, τ) = ω_{0} x

and

B (x, τ) = σ_{0} x

into equation (11) we get the stationary solution:

f (x) \propto x^{- β - 1},

(14)

which is a Pareto distribution, where

β = \frac{- (ω_{0} - \frac{σ_{0}^{2}}{2}) + \sqrt{{(ω_{0} - \frac{σ_{0}^{2}}{2})}^{2} + 2 σ_{0}^{2} δ}}{σ_{0}^{2}}

. The cumulative distribution of equation (14) is equation (6).

To eliminate the Matthew effect in income accumulation, we assume

A (x, τ) = ω_{0}

and

B (x, τ) = σ_{0}

. Then equation (9) is written as:

d x = ω_{0} d τ + σ_{0} d W (τ),

(15)

which indicates that the increment of the expected value of an agent’s income yields

d E [x] = ω_{0} d τ

that has nothing to do with the agent’s current income

E [x]

. In other words, each agent has an identical expected increment of income in the future. This implies equal opportunities of income acquisition among agents. Substituting

A (x, τ) = ω_{0}

and

B (x, τ) = σ_{0}

into equation (11) it is easy to get the stationary solution:

f (x) \propto e x p (- \frac{x}{θ}),

(16)

which is an exponential distribution, where

θ = \frac{σ_{0}^{2}}{{- ω}_{0} + \sqrt{ω_{0}^{2} + 2 σ_{0}^{2} δ}}

. The cumulative distribution of equation (16) is equation (2).

Within the framework of the random growth theory, the setting for

A (x, τ) = ω_{0}

and

B (x, τ) = σ_{0}

implies an ideal society in which the future earning of each agent has nothing to do with the agent’s past income accumulation. In a real society, such a setting may be undermined. For example, the Matthew effect in income accumulation would break this setting. However, we next empirically show that, for a market-economy country, the income structure of the low- and middle-income class, which occupies the majority of the populations, can be approximately described by an exponential distribution.

4. Empirical evidence

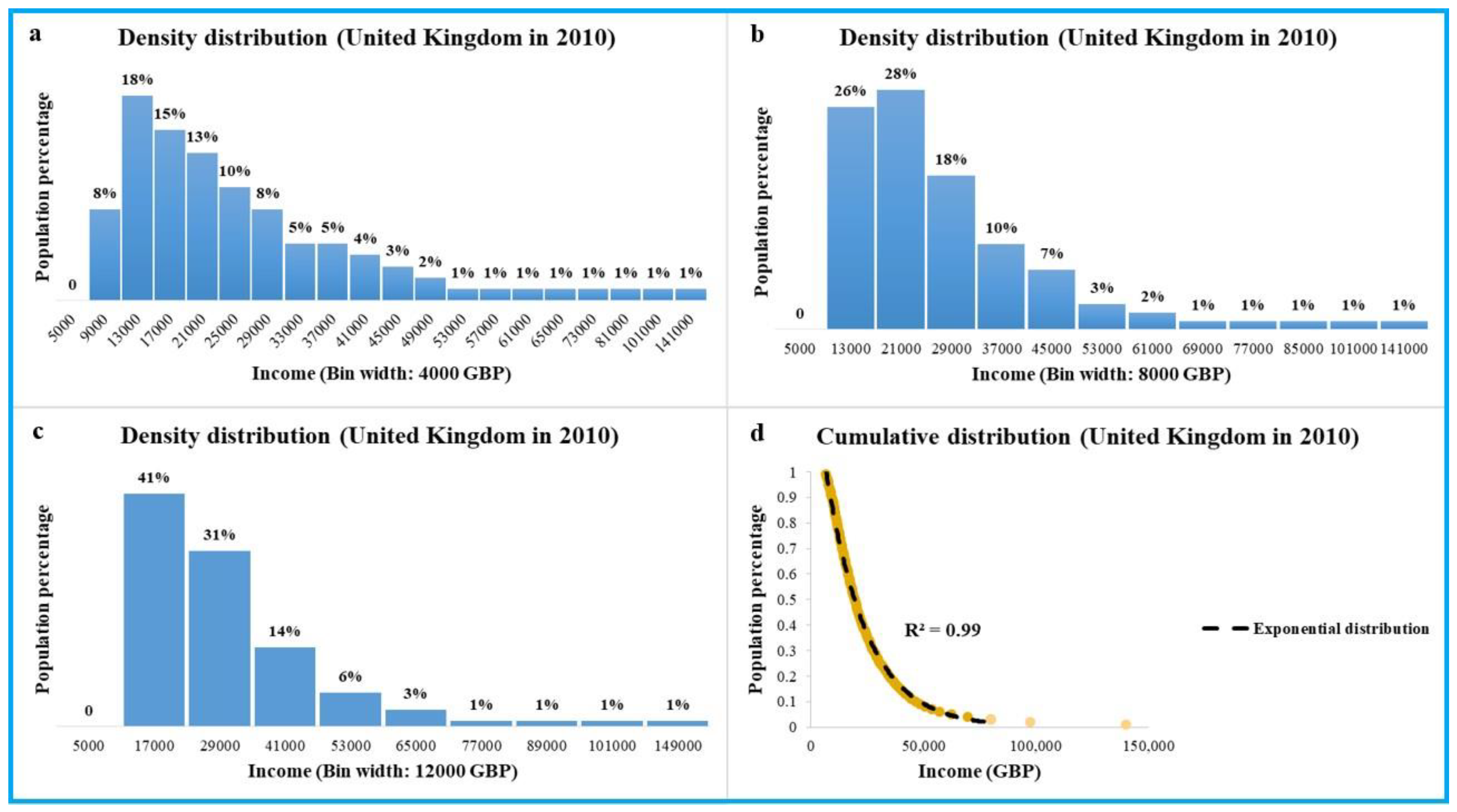
There has been a large body of empirical literature to support the coexistence between exponential income distribution and Pareto income distribution (Dragulescu and Yakovenko, 2001; Nirei and Souma, 2007; Newby et al., 2011; Prinz, 2016; Shaikh, 2017; Irwin and Irwin, 2017; Rosser, 2019; Tao et al., 2019; Ma and Ruzic, 2020; Lim and Min, 2020). However, there is scant empirical evidence for supporting the potential connection between the emergence of an exponential income distribution and the rise of a market economy. In this paper, we employ the household income data from four representative market-economy countries to investigate this connection. The four countries include three typical developed economies (the United Kingdom, the United States, and Canada) and one developing economy (China) that is the world’s second largest economy. In particular, because China is a special sample that has undergone the transition from a centrally planned economy to a market economy, it is interesting to check if there is a transition towards an exponential income distribution after the market-oriented economic reformation. Here, we first demonstrate that it is more reasonable to analyze the household income data by using the cumulative distribution function, rather than the density distribution function. To this end, we show that when one employs the density distribution function to analyze the household income data, the results may be inconsistent. In Figure 1, we use the household income data from the United Kingdom in 2010 to show this inconsistency: The shape of the density distribution of income may depend on the bin width of the histogram. For example, when the bin width is denoted by 4000 GBP, Figure 1a shows a right-skewed density distribution with a peak, which is close to a Log-normal distribution or a Gamma distribution. Unfortunately, when the bin width is increased to 8000 GBP, as shown in Figure 1b, the shape of density distribution begins to deviate from the pattern of a Log-normal distribution or a Gamma distribution. In particular, when the bin width is increased to 12000 GBP, the shape of density distribution turns to a monotonic function, see Figure 1c. This means that, for the same data, density distribution may lead to inconsistent graphs. However, when one uses the cumulative distribution function to describe the household income data, there are no such inconsistencies. Figure 1d shows that the great majority of populations in the United Kingdom obeys the exponential income distribution (2), which is a cumulative distribution function. Henceforth, we therefore employ the cumulative distribution function to analyze the household income data.

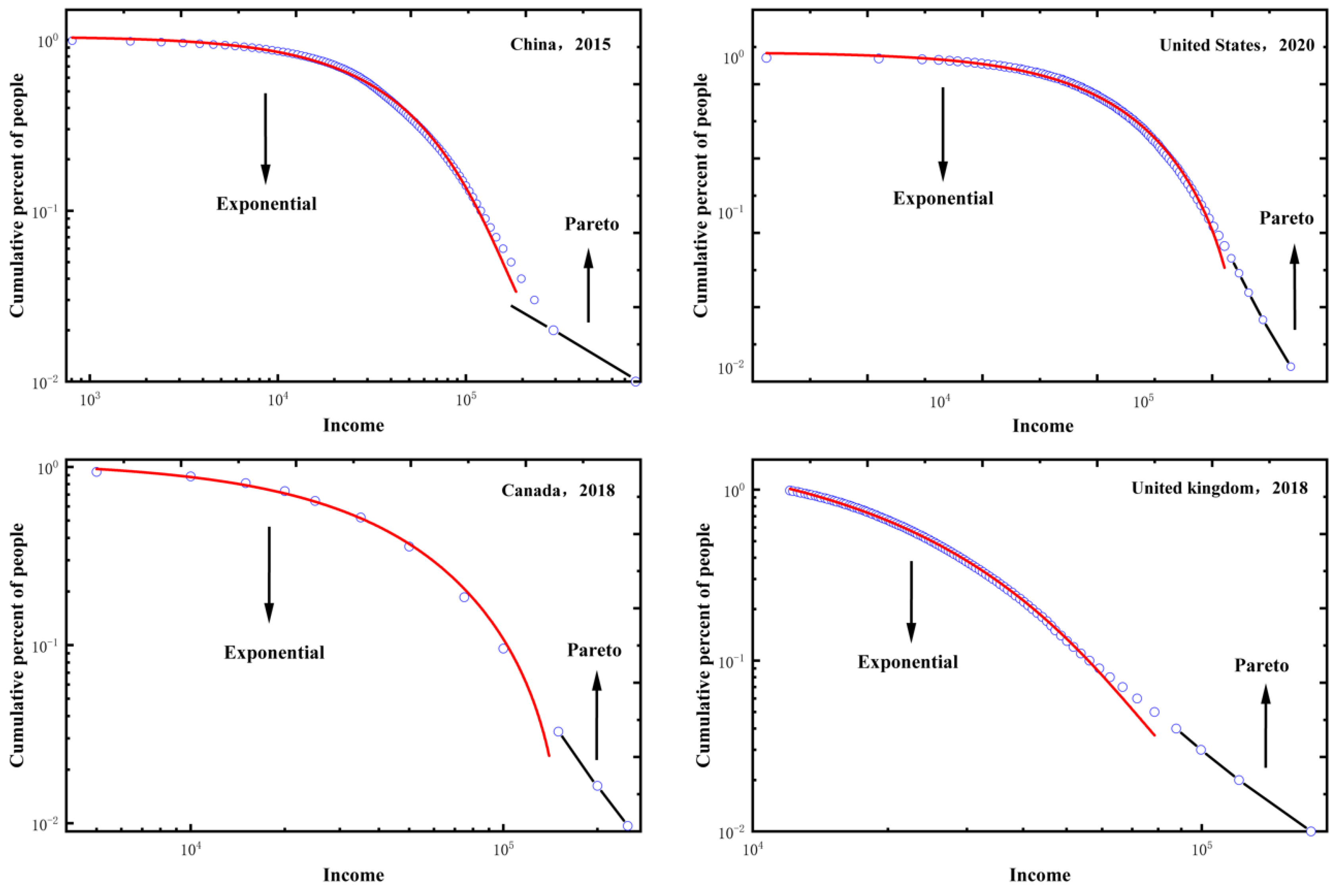
Because Dragulescu and Yakovenko (2001), Yakovenko and Rosser (2009), and Tao et al (2019) had employed the data from China (since 2013), the United Kingdom (since 1994), Canada (since 2012), and the United States (since 1983) to observe the emergence of a two-class income structure that was linked by exponential and Pareto parts, here we selected the dataset from the latest year available for four countries4. Figure 2 shows that the income structures of China (up to 2015), the United Kingdom (up to 2018), Canada (up to 2018), and the United States (up to 2020) uniformly exhibit a two-class pattern in which the low- and middle-income class obeys the exponential income distribution (2) and the top income class follows the Pareto distribution (6), where the cumulative distributions of income are shown on log-log scales to distinguish between exponential and Pareto distributions. The empirical observation supports the exponential income distribution as a stylized feature of the income structure of the low- and middle-income class, which occupies the great majority of the populations, in a market-economy country. 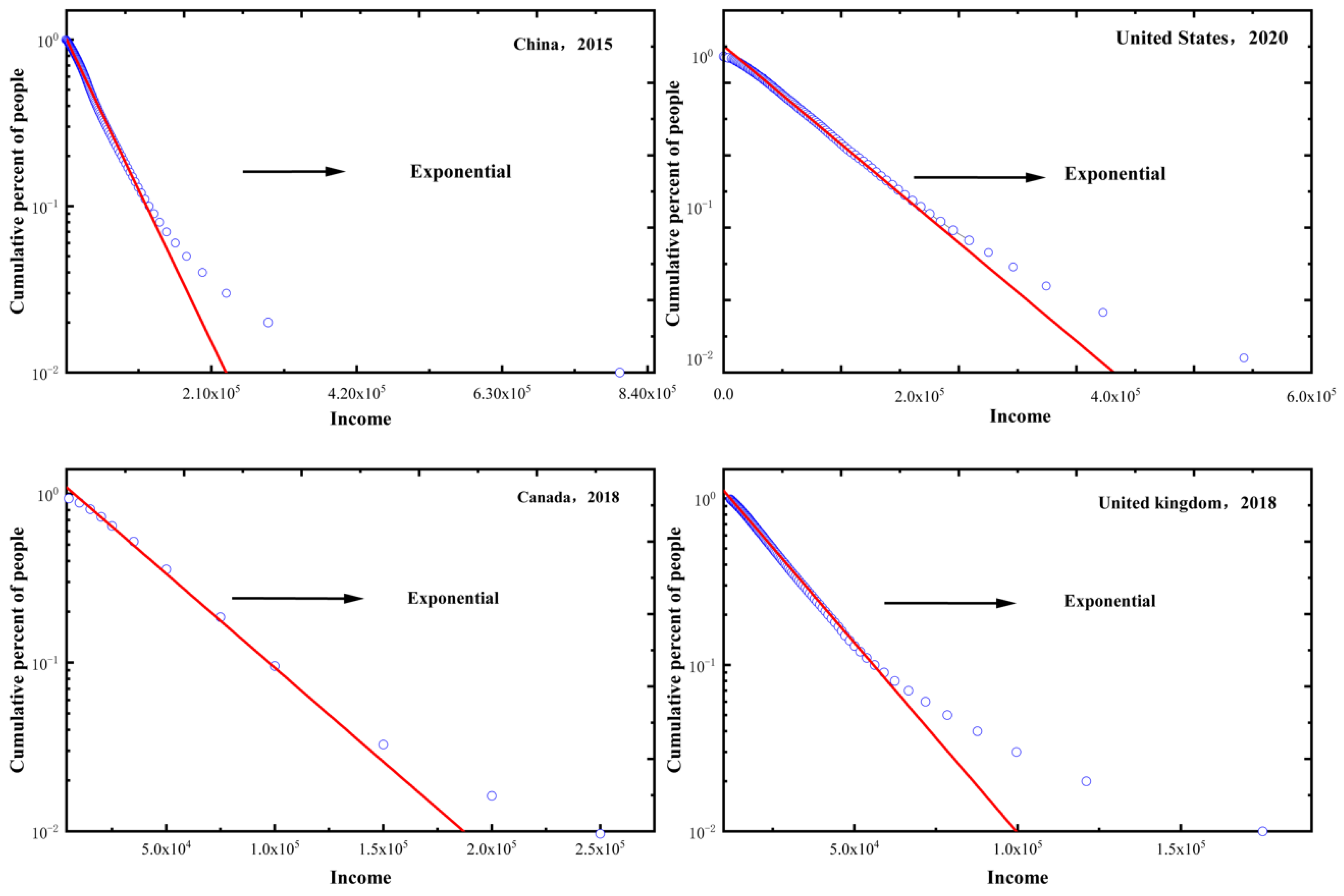In Figure 3, we further use the semi-log scale (vertical axis) to independently show the fitting effect of exponential distribution to the data of the low- and middle-income class for these four countries, respectively, where the exponential distribution is presented as a straight line.

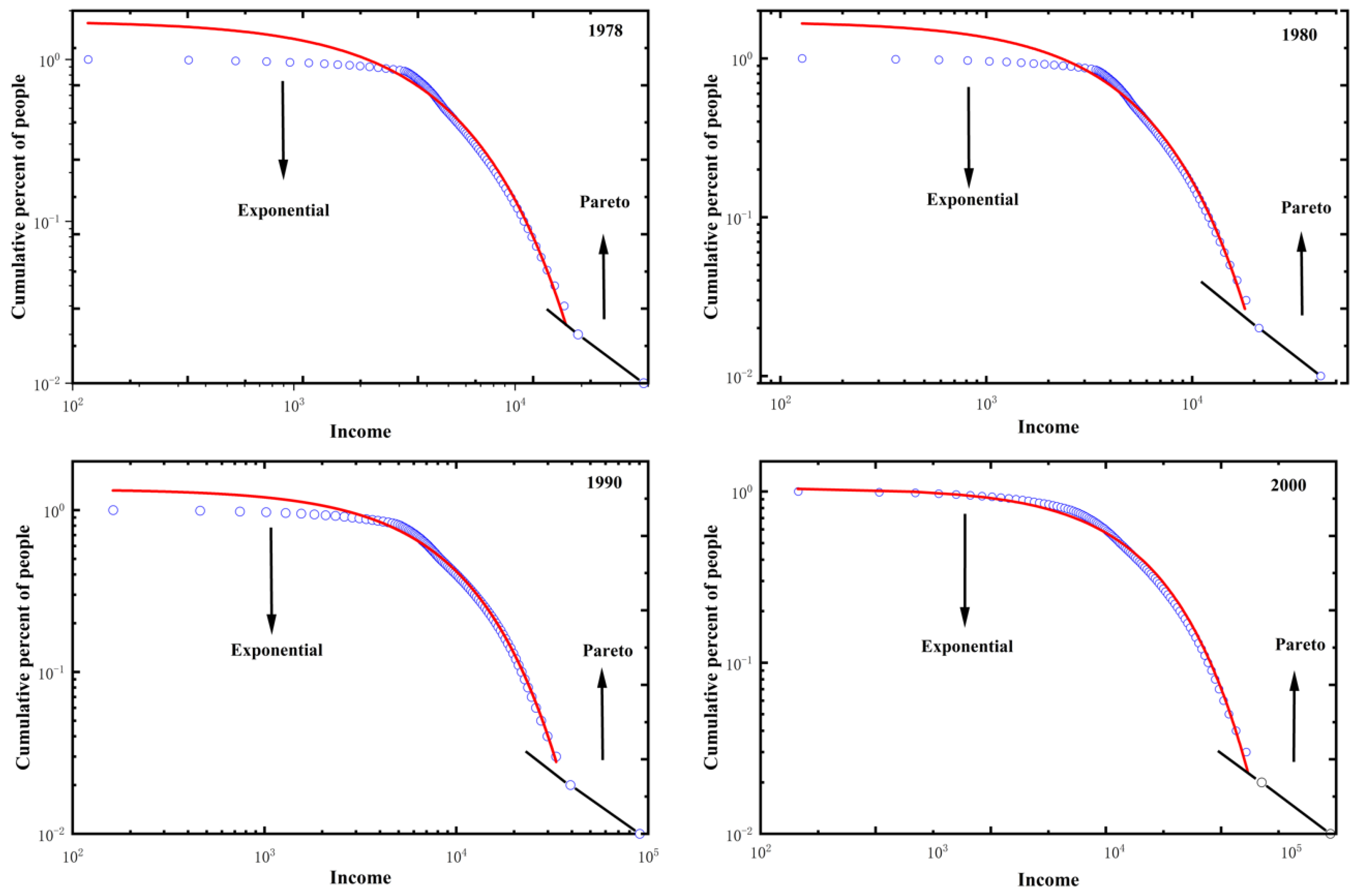
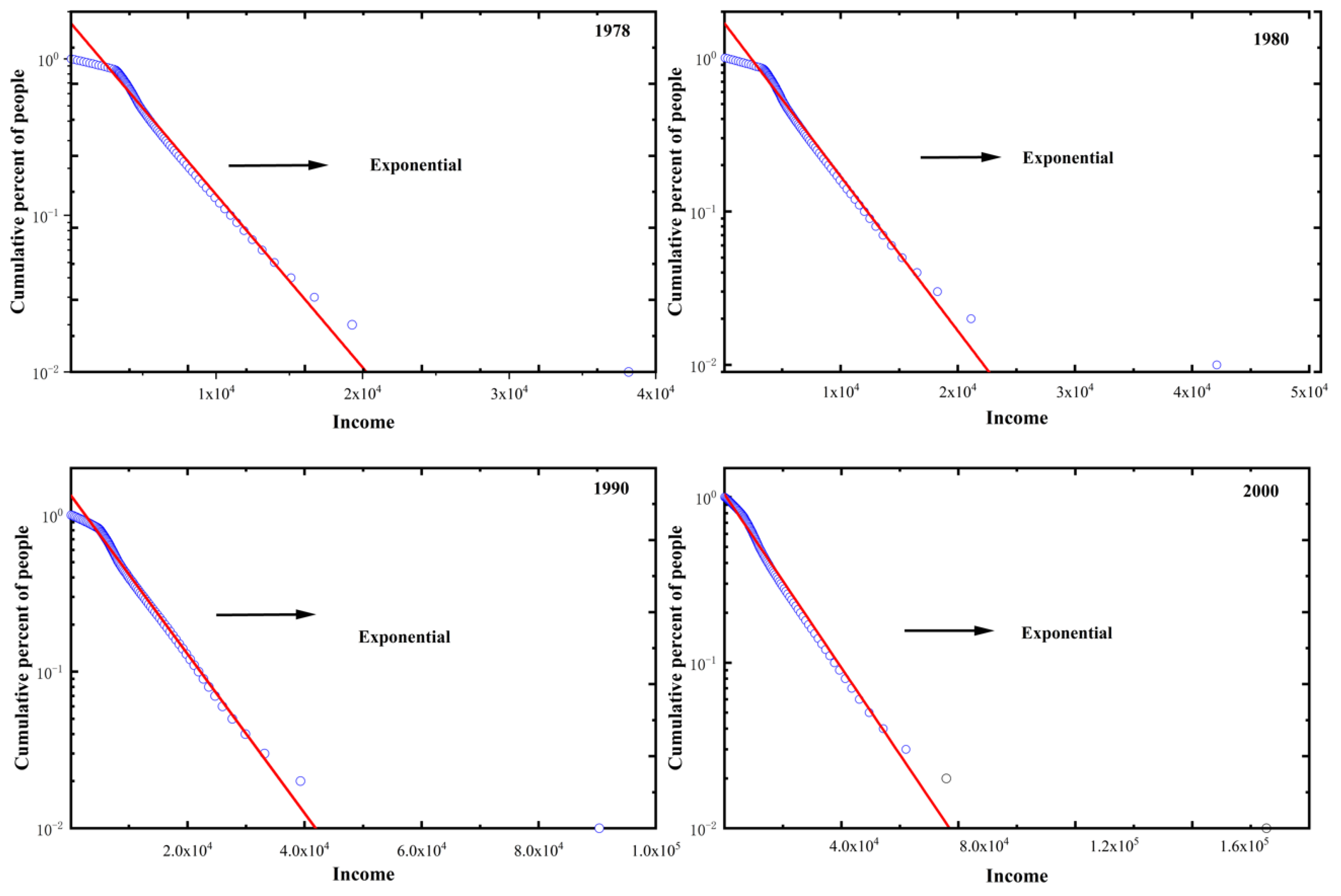
Differing from the existing literature, we particularly selected the household income data of China from 1978 to 2000 to demonstrate that the emergence of an exponential income distribution is relevant with the rise of a market economy. This period of time covers the main stages of China’s market-oriented economic reformation. In Figure 4, we empirically show that the income structure of the low- and middle-income class in China gradually evolved to an exact exponential distribution from the 1990s to the 2000s. By contrast, the low- and middle-income class in China around the 1990s only approximately obeyed the exponential income distribution, while the income structures in 1978 and 1980 radically differed from the exponential distribution. In Figure 5, we further use the semi-log scale (vertical axis) to independently show the fitting effect of exponential distribution to the data of the low- and middle-income class for China, where the exponential distribution is presented as a straight line. This is strong evidence for supporting the relevance of the exponential income distribution to the rise of a market economy.

5. Discussion

Here, we employ the random growth theory of income distribution (Gabaix, 1999; Gabaix et al., 2016; Aoki and Nirei, 2017; Jones and Kim, 2018) to provide a possible explanation for why the income structure of a market-economy country is approximately described by a two-class distribution functions. It is well known that Gibrat’s law for income dynamics leads to the Pareto tail of income distribution (Gabaix, 1999; Gabaix et al., 2016; Aoki and Nirei, 2017; Jones and Kim, 2018), which describes the top income class. This law tries to illustrate that the increment of the expected value of an agent’s income is equal to

d E [x] = ω_{0} E [x] d τ

, namely, equation (13). Thus far, Gibrat’s law is still an assumption. It may be suitable for the top income class. However, there is no solid evidence for supporting that Gibrat’s law governs the low- and middle-income class. In fact, there has been a large volume of empirical literature in testing the validity of Gibrat’s law by using the data of firm size (Almus, 2000; Becchetti and Trovato, 2002; Santarelli, et al., 2006). If we denote a firm’s size by

x

, then Gibrat’s law indicates

d x / x ~ ω_{0} d τ

, which means that the growth rate of a firm’s size is irrelevant with its current size

x

. Nevertheless, it has been empirically found that Gibrat’s law is not rejected for large firms, while it does not hold for small and medium sized firms (Almus, 2000; Becchetti and Trovato, 2002; Santarelli, et al., 2006). In this regard, the empirical investigations (Almus, 2000; Becchetti and Trovato, 2002) show that smaller firms have larger growth rate than larger ones; that is, for the small and medium sized firms, the growth rate of size,

\frac{d x}{d τ} / x

, should be a decreasing function with respect to the size

x

(namely, smaller firms have larger growth rate). Following this empirical finding, we simply assume for all the firms

d x / x ~ x^{a - 1} d τ,

(17)

where

0 \leq a \leq 1

When

a = 1

, equation (17) becomes Gibrat’s law, which holds for the large firms. When

0 \leq a < 1

, equation (17) agrees with the empirical investigations (Almus, 2000; Becchetti and Trovato, 2002) that require smaller firms to have larger growth rate. Now, we assume that equation (17) holds for households’ income as well. Thus, we propose to modify equation (12) as10

d x = ω_{0} x^{a} d τ + σ_{0} x^{a} d W (τ) .

(18)

By equation (18), it is easy to obtain

d E [x] = ω_{0} E [x^{a}] d τ,

(19)

which agrees with equation (17).

Equation (19) means that the increment of the expected value of an agent’s income,

d E [x]

, depends on

E [x^{a}]

, which characterizes the Matthew effect in income accumulation as long as

a > 0

. For example, as

a \to 1

, the Matthew effect become stronger, and as

a \to 0

, the Matthew effect become weaker. In particular, when

a = 0

, the Matthew effect vanishes and each agent has an identical expected increment of income in the future. This indicates that

a = 0

corresponds to a perfect market economy, which equalizes opportunities for income acquisition among citizens. However, a real market economy is not so perfect, and it instead may lead to the inequality of opportunity, i.e.,

a > 0

. As such, for an imperfect market economy, we anticipate that

a

would become larger for the high-income population; for instance, if an agent is richer, by using the advantage of wealth this agent might become more capable in breaking the rules of fair competition, so as to enlarge

a

(for pursuing higher earnings). At this rate, as

a \to 1

, the income distribution yields a Pareto law, which accounts for our empirical observation for the top income class, as shown in Figure 2. By contrast, the low-income families are less capable to enlarge

a

, and this in turn leads to less opportunities for pursuing earnings. At this rate, as

a \to 0

, the income distribution yields an exponential pattern, which accounts for our empirical observation for the low- and middle-income class, as shown in Figure 2. However, if the market economy is perfectly competitive,

a

will stay at zero to guarantee the equality of opportunity. Then, nobody can use the advantage of wealth to break the rules of fair competition. As is well known, the institutional arrangement of a free-market economy is to establish an equal-opportunity market competition system. This means that, with the establishment of a market economy, we anticipate that the income structure of a part of the population would evolve to an exponential pattern. In particular, along with the further improvement of a market economy, we anticipate that the proportion of exponential-distribution families would be enlarged. This accounts for our empirical observation for China from 1978 to 2000, as shown in Figure 4.

However, it is important to stress that the emergence of an exponential income structure does not indicate an exponential probability distribution of income. Conversely, the latter can lead to the former. Therefore, we propose to identify the emergence of an exponential income distribution as a potential necessary condition for equalizing opportunities for income acquisition among citizens. In fact, there are other conditions to guarantee the equality of opportunity together. For example, to promote an exponential income structure to an exponential probability distribution of income, social and economic mobility11 should be allowed. Despite this, if the exponential income structure is broken, by equation (1) we must deduce that the probability distribution of income has “memories” for certain persons, which might break equal opportunities of income acquisition. On the other hand, even if social and economic mobility is allowed, if the probability distribution of income goes against the memoryless property (1), then the equal opportunities of income acquisition still cannot be guaranteed. For example, social and economic mobility is allowed, but then the probability distribution of income acquisition is denoted by the Pareto law (6), which, by equation (7), leads to the inequality of opportunity.

6. Conclusion

In this paper, we have shown that, if the exponential distribution dominates an economy as a probability distribution of income acquisition, then the memoryless property imposes equal opportunities on agents in this economy to acquire earnings. As such, the exponential income distribution can serve as a potential necessary condition for equalizing opportunities for income acquisition among citizens. To validate the relationship between exponential distribution and equal opportunity, we particularly employ the household income data of China from 1978 to 2015 to demonstrate that the emergence of an exponential income distribution is relevant with the rise of a market economy. This period of time covers the main stages of China’s market-oriented economic reformation. Our investigation shows that the income structure of the low- and middle-income class in China gradually evolved to an exponential distribution after the market-oriented economic reformation. This is strong evidence that the emergence of an exponential income distribution is related to weakening of some monopoly power, where we identify a centrally planned economy as a certain kind of state monopoly. In the process of transition from a centrally planned economy to a market economy, the most essential change is to establish an equal-opportunity market competition system, which will help to reduce the state monopoly. In this sense, the emergence of an exponential distribution implies its connection with equal opportunity.

However, the emergence of an exponential income structure does not indicate an exponential probability distribution of income. Only the latter has the memoryless property. Therefore, we propose to identify the emergence of an exponential income distribution as a potential necessary condition for equalizing opportunities for income acquisition among citizens. In fact, there should be some other conditions of promoting the equality of opportunity together. For example, to promote an exponential income structure to an exponential probability distribution of income, social and economic mobility should be allowed. Despite this, if the exponential income structure is broken, by equation (1) we must deduce that the probability distribution of income has “memories” for certain persons, which might break equal opportunities of income acquisition. On the other hand, even if social and economic mobility is allowed, if the probability distribution of income goes against the memoryless property (1), then the equal opportunities of income acquisition still cannot be guaranteed. For example, social and economic mobility is allowed, but then the probability distribution of income acquisition is denoted by the Pareto law (6), which, by equation (7), leads to the inequality of opportunity.

Author Contributions

The author performed the research in this paper independently.

Data Availability Statement

This study analyzed publicly available datasets. These datasets can be accessed here: Data resource for China: http://wid.world/data/; Data resource for the United States: https://ipums.org/; Data resource for Canada: https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1110000801; Data resource for the United Kingdom: https://www.gov.uk/government/statistics/percentile-points-from-1-to-99-for-total-income-before-and-after-tax.

Acknowledgments

This article is dedicated to my mother.

Conflicts of Interest

The author declares no conflict of interest.

Notes

1	Equation (1) is referred to as the “memoryless property”. For the income distribution, we propose to identify equation (1) as the benchmark process of equal opportunities for income acquisition.
2	If we replace $t$ by $t^{'} - μ$ and $X + μ$ by $X^{'}$ , respectively, then the exponential distribution (2) can be generally written as the 2-parameter form $P (X^{'} \geq t^{'}) = e x p (- \frac{t^{'} - μ}{θ})$ , where $t^{'} \geq μ$ . This indicates that the 2-parameter exponential distribution likewise satisfies the memoryless property (1); that is, equation (1) is invariable under the translation transformations $s \to s^{'} - μ$ and $t \to t^{'} - μ$ . However, for simplicity, in this paper we only use the 1-parameter form (2) to show the relationship between exponential income distribution and equal opportunity.
3	Data resource for the United Kingdom: https://www.gov.uk/government/statistics/percentile-points-from-1-to-99-for-total-income-before-and-after-tax
4	The data analyses were performed in 2022.
5	Data resource for China: http://wid.world/data/
6	Data resource for the United States: https://ipums.org/
7	Data resource for Canada: https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1110000801
8	Data resource for the United Kingdom: https://www.gov.uk/government/statistics/percentile-points-from-1-to-99-for-total-income-before-and-after-tax
9	Data resource for China: http://wid.world/data/
10	Obviously, there are many possible differential forms that relate equation (12) to equation (15) by using the parameter $a$ . For example, one can construct a convex differential form $d x = [(1 - a) ω_{0} + a ω_{c} x] d τ + [(1 - a) σ_{0} + a σ_{c} x] d W (τ)$ , where $ω_{c}$ and $σ_{c}$ are two constants. When $a = 0$ , it becomes equation (15) and when $a = 1$ , it becomes equation (12). It is easy to check that the convex differential form satisfies the empirical findings (Almus, 2000; Becchetti and Trovato, 2002) that require smaller firms to have larger growth rate. That is, we have $\frac{d E [x]}{E [x]} = [\frac{(1 - a) ω_{0}}{E [x]} + a ω_{c}] d τ$ . In particular, when $0 < a < 1$ , it yields $\frac{d E [x]}{E [x]} = \frac{(1 - a) ω_{0}}{E [x]} d τ$ for $E [x] \to 0$ and yields $\frac{d E [x]}{E [x]} = a ω_{c} d τ$ for $E [x] \to \infty$ . This means that the convex differential form would lead to an exponential distribution for low $x$ and lead to a Pareto distribution for high $x$ .
11	There is a large body of literature of studying social and economic mobility (Jantti and Jenkins, 2015; Stojkoski, 2022; Stojkoski et al., 2022).

References

Abul-Magd, A. Y. (2002): Wealth distribution in an ancient Egyptian society. Physical Review E 66, 057104.
Almus, M. (2000): Testing “Gibrat’s Law” for Young Firms – Empirical Results for West Germany. Small Business Economics 15, 1-12.
Angle, J. (1993): Deriving the Size Distribution of Personal Wealth from “The Rich Get Richer, the Poor Get Poorer”. Journal of Mathematical Sociology 18, 27-46.
Aoyama, H., Souma,W., Nagahara, Y., Okazaki, M. P., Takayasu, H., and Takayasu, M. (2000): Pareto’s law for income of individuals and debt of bankrupt companies. Fractals 8, 293-3000.
Aoki, S. and Nirei, M. (2017): Zipf’s Law, Pareto’s Law, and the Evolution of Top Incomes in the United States. American Economic Journal: Macroeconomics, 9, 36-71.
Arrow, K. J. and Debreu, G. (1954): Existence of an Equilibrium for a competitive economy. Econometrica 22, 265-290.
Atkinson, A. B., Piketty, T., and Saez, E. (2011): Top Incomes in the Long Run of History. Journal of Economic Literature 49, 3-71.
Becchetti, L. and Trovato, G. (2002): The Determinants of Growth for Small and Medium Sized Firms. The Role of the Availability of External Finance. Small Business Economics 19, 291–306.
Benhabib, J., Bisin, A. and Zhu, S. (2011): The Distribution of Wealth and Fiscal Policy in Economies With Finitely Lived Agents. Econometrica, 79, 123-157.
Champernowne, D. G. (1953): A Model of Income Distribution. Economic Journal 63, 318-351.
Dragulescu, A. and Yakovenko, V. M. (2001): Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Physica A 299, 213-221.
Gabaix, X. (1999): Zipf’s Law for Cities: An Explanation. Quarterly Journal of Economics 114, 739-767.
Gabaix, X. et al. (2016): The Dynamics of Inequality. Econometrica 84, 2071–2111.
Hegyi, G., Neda, Z., and Santos, M. A. (2007): Wealth distribution and Pareto’s law in the Hungarian medieval society. Physica A 380, 271-277.
Huang, J. S. (1981): On a “lack of memory” property. Annals of the Institute of Statistical Mathematics 33, 131-134.
Irwin. R. J. and Irwin, T. C. (2017): Stability of an exponential distribution for New Zealand taxable personal income. New Zealand Economic Papers 51, 49-59.
Jantti, M. and Jenkins, S. P. (2015): Income mobility. Handbook of Income Distribution 2, 807-935.
Jones, C. I. and Kim, J. (2018): A Schumpeterian Model of Top Income Inequality. Journal of Political Economy 126, 1785-1826.
Lim, G. and Min, S. (2020): Analysis of Solidarity Effect for Entropy, Pareto, and Gini Indices on Two-Class Society Using Kinetic Wealth Exchange Model. Entropy 22, 386.
Lux, T. and Marchesi, M. (1999): Scaling and criticality in a stochastic multi-agent model of a financial market, Nature 397, 498-500.
Ma, L. and Ruzic, D. (2020): Globalization and top income shares. Journal of International Economics 125, 103312.
Malevergne, Y., Saichev A., and Sornette, D. (2013): Zipf’s law and maximum sustainable growth. Journal of Economic Dynamics and Control 37, 1195-1212.
Mandelbrot, B. (1960): The Pareto-Levy law and the distribution of income. International Economic Review 1, 79-106.
Marsaglia, G. and Tubilla, A. (1975): A note on the “lack of memory” property of the exponential distribution, Annals of Probability 3, 353-354.
Newby, M., Behr, A., and Feizabadi, M. S. (2011): Investigating the distribution of personal income obtained from the recent U.S. data. Economic Modelling 28, 1170-1173.
Nirei, M. and Souma, W. (2007): A Two Factor Model of Income Distribution Dynamics. Review of Income and Wealth 53, 440-459.
Pareto, V. (1897): Cours d’ Economie Politique. L’ Universite de Lausanne.
Prinz, A. (2016): Do capitalistic institutions breed billionaires? Empirical Economics 51, 1319-1332.
Rawls, J. (1999): A theory of justice (Revised Edition). Harvard University Press, Cambridge.
Rosser, J. B. (2019): The Minsky moment as the revenge of entropy. Macroeconomic Dynamics 24, 7-23.
Saichev, A., Malevergne, Y. and Sornette, D. (2009): Theory of Zipf’s Law and beyond, Lecture Notes in Economics and Mathematical Systems, Volume 632, Springer.
Santarelli, et al. (2006): Gibrat’s Law: An Overview of the Empirical Literature. In: Santarelli, E. (eds) Entrepreneurship, Growth, and Innovation. International Studies in Entrepreneurship, vol 12. Springer, Boston, MA. https://doi.org/10.1007/0-387-32314-7_3.
Shaikh, A. (2017): Income distribution, econophysics and Piketty. Review of Political Economy 29, 18-29.
Shimizu, R. (1979): On a lack of memory property of the exponential distribution. Annals of the Institute of Statistical Mathematics 31, 309-313.
Souma, W. (2002): Empirical Science of Financial Fluctuations: The Advent of Econophysics, Springer, Tokyo.
Stojkoski, V. (2022): Measures of physical mixing evaluate the economic mobility of the typical individual. arXiv: 2205.02800.
Stojkoski, V. et al. (2022): Income inequality and mobility in geometric Brownian motion with stochastic resetting: theoretical results and empirical evidence of non-ergodicity. Philosophical Transactions of the Royal Society A 380, 20210157.
Tao, Y. (2016): Spontaneous economic order, Journal of Evolutionary Economics 26, 467-500.
Tao, Y., Wu, X., Zhou, T., Yan, W., Huang, Y., Yu, H., Mondal, B., and Yakovenko, V. M. (2019): Exponential structure of income inequality: evidence from 67 countries. Journal of Economic Interaction and Coordination 14, 345-376.
Tao, Y. (2021): Exponential Income Distribution and Evolution of Unemployment Compensation in the United Kingdom. Preprints 2021, 2021070350 (doi: 10.20944/preprints202107.0350.v1).
Tao, Y., Sornette, D., and Lin, L. (2021): Emerging social brain: a collective self-motivated Boltzmann machine. Chaos, Solitons & Fractals 143, 110543.
Wold, H. O. A. and Whittle, P. (1957): A Model Explaining the Pareto Distribution of Wealth. Econometrica, 25, 591-595.
Yakovenko, V. M. and Rosser, J. B. (2009): Statistical mechanics of money, wealth, and income. Reviews of Modern Physics 81, 1703-1725.

Figure 1. Density distribution may lead to inconsistent graphs3. a: When the bin width is denoted by 4000 GBP, the histogram of density distribution is a right-skewed graph with a peak, which is close to a Log-normal distribution or a Gamma distribution. b: When the bin width is increased to 8000 GBP, the histogram of density distribution begins to deviate from a Log-normal distribution or a Gamma distribution. c: When the bin width is increased to 12000 GBP, the histogram of density distribution turns to a monotonic function. d: The cumulative distribution of income obeys an exponential function.

Figure 2. A larger proportion of populations is evolving towards an exponential income distribution. The low- and middle-income class (about 97% of populations) in China obeys an exponential income distribution5 (currency unit: CNY). The low- and middle-income class (about 95% of populations) in the United States obeys an exponential income distribution6 (currency unit: USD). The low- and middle-income class (about 97% of populations) in Canada obeys an exponential income distribution7 (currency unit: USD). The low- and middle-income class (about 95% of populations) in the United Kingdom obeys an exponential income distribution8 (currency unit: GBP). For the four countries, the top income class obeys the Pareto distribution.

Figure 3. The fitting effect of exponential distribution to the data of the low- and middle-income class for four countries is shown by using semi-log scale (vertical axis).

Figure 4. The income structure of the low- and middle-income class in China gradually evolved to an exponential distribution after the market-oriented economic reformation9.

Figure 5. The fitting effect of exponential distribution to the data of the low- and middle-income class for China is shown by using semi-log scale (vertical axis).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Memoryless Property of the Income Distribution as an Indication for Testing the Equality of Opportunity: Evidence from China (1978-2015)

Abstract

1. Introduction

2. Memoryless property and exponential income distribution

3. Income dynamics

4. Empirical evidence

5. Discussion

6. Conclusion

Author Contributions

Data Availability Statement

Acknowledgments

Conflicts of Interest

Notes

References

MDPI Initiatives

Important Links

Subscribe