Neutrosophic 1-Failed SuperHyperForcing in the SuperHyperFunction To Use Neutrosophic SuperHyperGraphs on Cancer’s Neutrosophic Recognition And Beyond

1. Background

There are some researches covering the topic of this research. In what follows, there are some discussion and literature reviews about them.

First article is titled “properties of SuperHyperGraph and neutrosophic SuperHyperGraph” in Ref. [1] by Henry Garrett (2022). It’s first step toward the research on neutrosophic SuperHyperGraphs. This research article is published on the journal “Neutrosophic Sets and Systems” in issue 49 and the pages 531-561. In this research article, different types of notions like dominating, resolving, coloring, Eulerian(Hamiltonian) neutrosophic path, n-Eulerian(Hamiltonian) neutrosophic path, zero forcing number, zero forcing neutrosophic- number, independent number, independent neutrosophic-number, clique number, clique neutrosophic-number, matching number, matching neutrosophic-number, girth, neutrosophic girth, 1-zero-forcing number, 1-zero- forcing neutrosophic-number, failed 1-zero-forcing number, failed 1-zero-forcing neutrosophic-number, global- offensive alliance, t-offensive alliance, t-defensive alliance, t-powerful alliance, and global-powerful alliance are defined in SuperHyperGraph and neutrosophic SuperHyperGraph. Some Classes of SuperHyperGraph and Neutrosophic SuperHyperGraph are cases of research. Some results are applied in family of SuperHyperGraph and neutrosophic SuperHyperGraph. Thus this research article has concentrated on the vast notions and introducing the majority of notions.

The seminal paper and groundbreaking article is titled “neutrosophic co-degree and neutrosophic degree alongside chromatic numbers in the setting of some classes related to neutrosophic hypergraphs” in Ref. [2] by Henry Garrett (2022). In this research article, a novel approach is implemented on SuperHyperGraph and neutrosophic SuperHyperGraph based on general forms without using neutrosophic classes of neutrosophic SuperHyperGraph. It’s published in prestigious and fancy journal is entitled “Journal of Current Trends in Computer Science Research (JCTCSR)” with abbreviation “J Curr Trends Comp Sci Res” in volume 1 and issue 1 with pages 06-14. The research article studies deeply with choosing neutrosophic hypergraphs instead of neutrosophic SuperHyperGraph. It’s the breakthrough toward independent results based on initial background.

In some articles are titled “(Neutrosophic) SuperHyperModeling of Cancer’s Recognitions Featuring (Neutrosophic) SuperHyperDefensive SuperHyperAlliances” in Ref. [3] by Henry Garrett (2022), “(Neutrosophic) SuperHyperAlliances With SuperHyperDefensive and SuperHyperOffensive Type-SuperHyperSet On (Neutrosophic) SuperHyperGraph With (Neutrosophic) SuperHyperModeling of Cancer’s Recognitions And Related (Neutrosophic) SuperHyperClasses” in Ref. [4] by Henry Garrett (2022), “SuperHyperGirth on SuperHyperGraph and Neutrosophic SuperHyperGraph With SuperHyperModeling of Cancer’s Recognitions” in Ref. [5] by Henry Garrett (2022), “Some SuperHyperDegrees and Co-SuperHyperDegrees on Neutrosophic SuperHyperGraphs and SuperHyperGraphs Alongside Applications in Cancer’s Treatments” in Ref. [6] by Henry Garrett (2022), “SuperHyperDominating and SuperHyperResolving on Neutrosophic SuperHyperGraphs And Their Directions in Game Theory and Neutrosophic SuperHyperClasses” in Ref. [7] by Henry Garrett (2022), “Basic Notions on (Neutrosophic) SuperHyperForcing And (Neutrosophic) SuperHyperModeling in Cancer’s Recognitions And (Neutrosophic) SuperHyperGraphs” in Ref. [8] by Henry Garrett (2022), “Basic Neutrosophic Notions Concerning SuperHyperDominating and Neutrosophic SuperHyperResolving in SuperHyperGraph” in Ref. [9] by Henry Garrett (2022), “Initial Material of Neutrosophic Preliminaries to Study Some Neutrosophic Notions Based on Neutrosophic SuperHyperEdge (NSHE) in Neutrosophic SuperHyperGraph (NSHG)” in Ref. [10] by Henry Garrett (2022), there are some endeavors to formalize the basic SuperHyperNotions about neutrosophic SuperHyperGraph and SuperHyperGraph.

Some studies and researches about neutrosophic graphs, are proposed as book in Ref. [11] by Henry Garrett (2022) which is indexed by Google Scholar and has more than 2347 readers in Scribd. It’s titled “Beyond Neutrosophic Graphs” and published by Ohio: E-publishing: Educational Publisher 1091 West 1st Ave Grandview Heights, Ohio 43212 United State. This research book covers different types of notions and settings in neutrosophic graph theory and neutrosophic SuperHyperGraph theory.

Also, some studies and researches about neutrosophic graphs, are proposed as book in Ref. [12] by Henry Garrett (2022) which is indexed by Google Scholar and has more than 3048 readers in Scribd. It’s titled “Neutrosophic Duality” and published by Florida: GLOBAL KNOWLEDGE - Publishing House 848 Brickell Ave Ste 950 Miami, Florida 33131 United States. This research book presents different types of notions SuperHyperResolving and SuperHyperDominating in the setting of duality in neutrosophic graph theory and neutrosophic SuperHyperGraph theory. This research book has scrutiny on the complement of the intended set and the intended set, simultaneously. It’s smart to consider a set but acting on its complement that what’s done in this research book which is popular in the terms of high readers in Scribd.

1.1. Motivation and Contributions

In this research, there are some ideas in the featured frameworks of motivations. I try to bring the motivations in the narrative ways. Some cells have been faced with some attacks from the situation which is caused by the cancer’s attacks. In this case, there are some embedded analysis on the ongoing situations which in that, the cells could be labelled as some groups and some groups or individuals have excessive labels which all are raised from the behaviors to overcome the cancer’s attacks. In the embedded situations, the individuals of cells and the groups of cells could be considered as “new groups”. Thus it motivates us to find the proper SuperHyperModels for getting more proper analysis on this messy story. I’ve found the SuperHyperModels which are officially called “SuperHyperGraphs” and “Neutrosophic SuperHyperGraphs”. In this SuperHyperModel, the cells and the groups of cells are defined as “SuperHyperVertices” and the relations between the individuals of cells and the groups of cells are defined as “SuperHyperEdges”. Thus it’s another motivation for us to do research on this SuperHyperModel based on the “Cancer’s Neutrosophic Recognition”. Sometimes, the situations get worst. The situation is passed from the certainty and precise style. Thus it’s the beyond them. There are three descriptions, namely, the degrees of determinacy, indeterminacy and neutrality, for any object based on vague forms, namely, incomplete data, imprecise data, and uncertain analysis. The latter model could be considered on the previous SuperHyperModel. It’s SuperHyperModel. It’s SuperHyperGraph but it’s officially called “Neutrosophic SuperHyperGraphs”. The cancer is the disease but the model is going to figure out what’s going on this phenomenon. The special case of this disease is considered and as the consequences of the model, some parameters are used. The cells are under attack of this disease but the moves of the cancer in the special region are the matter of mind. The neutrosophic recognition of the cancer could help to find some treatments for this disease. The SuperHyperGraph and neutrosophic SuperHyperGraph are the SuperHyperModels on the “Cancer’s Neutrosophic Recognition” and both bases are the background of this research. Sometimes the cancer has been happened on the region, full of cells, groups of cells and embedded styles. In this segment, the SuperHyperModel proposes some SuperHyperNotions based on the connectivities of the moves of the cancer in the forms of alliances’ styles with the formation of the design and the architecture are formally called “1-failed SuperHyperForcing” in the themes of jargons and buzzwords. The prefix “SuperHyper” refers to the theme of the embedded styles to figure out the background for the SuperHyperNotions. The neutrosophic recognition of the cancer in the long-term function. The specific region has been assigned by the model [it’s called SuperHyperGraph] and the long cycle of the move from the cancer is identified by this research. Sometimes the move of the cancer hasn’t be easily identified since there are some determinacy, indeterminacy and neutrality about the moves and the effects of the cancer on that region; this event leads us to choose another model [it’s said to be neutrosophic SuperHyperGraph] to have convenient perception on what’s happened and what’s done. There are some specific models, which are well-known and they’ve got the names, and some general models. The moves and the traces of the cancer on the complex tracks and between complicated groups of cells could be fantasized by a neutrosophic SuperHyperPath(-/SuperHyperCycle, SuperHyperStar, SuperHyperBipartite, SuperHyperMultipartite, SuperHyperWheel). The aim is to find either the optimal 1-failed SuperHyperForcing or the neutrosophic 1-failed SuperHyperForcing in those neutrosophic SuperHyperModels. Some general results are introduced. Beyond that in SuperHyperStar, all possible SuperHyperPaths have only two SuperHyperEdges but it’s not enough since it’s essential to have at least three SuperHyperEdges to form any style of a SuperHyperCycle. There isn’t any formation of any SuperHyperCycle but literarily, it’s the deformation of any SuperHyperCycle. It, literarily, deforms and it doesn’t form.

Question 1. 

How to define the SuperHyperNotions and to do research on them to find the “ amount of 1-failed SuperHyperForcing” of either individual of cells or the groups of cells based on the fixed cell or the fixed group of cells, extensively, the “amount of 1-failed SuperHyperForcing” based on the fixed groups of cells or the fixed groups of group of cells?

Question 2. 

What are the best descriptions for the “Cancer’s Neutrosophic Recognition” in terms of these messy and dense SuperHyperModels where embedded notions are illustrated?

It’s motivation to find notions to use in this dense model is titled “SuperHyperGraphs”. Thus it motivates us to define different types of “1-failed SuperHyperForcing” and “neutrosophic 1-failed SuperHyperForcing” on “SuperHyperGraph” and “Neutrosophic SuperHyperGraph”. Then the research has taken more motivations to define SuperHyperClasses and to find some connections amid this SuperHyperNotion with other SuperHyperNotions. It motivates us to get some instances and examples to make clarifications about the framework of this research. The general results and some results about some connections are some avenues to make key point of this research, “Cancer’s Neutrosophic Recognition”, more understandable and more clear.

The framework of this research is as follows. In the beginning, I introduce basic definitions to clarify about preliminaries. In the subsection “Preliminaries”, initial definitions about SuperHyperGraphs and neutrosophic SuperHyperGraph are deeply-introduced and in-depth-discussed. The elementary concepts are clarified and illustrated completely and sometimes review literature are applied to make sense about what’s going to figure out about the upcoming sections. The main definitions and their clarifications alongside some results about new notions, 1-failed SuperHyperForcing and neutrosophic 1-failed SuperHyperForcing, are figured out in sections “1-failed SuperHyperForcing” and “Neutrosophic 1-failed SuperHyperForcing”. In the sense of tackling on getting results and in order to make sense about continuing the research, the ideas of SuperHyperUniform and Neutrosophic SuperHyperUniform are introduced and as their consequences, corresponded SuperHyperClasses are figured out to debut what’s done in this section, titled “Results on SuperHyperClasses” and “Results on Neutrosophic SuperHyperClasses”. As going back to origin of the notions, there are some smart steps toward the common notions to extend the new notions in new frameworks, SuperHyperGraph and Neutrosophic SuperHyperGraph, in the sections “Results on SuperHyperClasses” and “Results on Neutrosophic SuperHyperClasses”. The starter research about the general SuperHyperRelations and as concluding and closing section of theoretical research are contained in the section “General Results”. Some general SuperHyperRelations are fundamental and they are well-known as fundamental SuperHyperNotions as elicited and discussed in the sections, “General Results”, “1-failed SuperHyperForcing”, “Neutrosophic 1-failed SuperHyperForcing”, “Results on SuperHyperClasses” and “Results on Neutrosophic SuperHyperClasses”. There are curious questions about what’s done about the SuperHyperNotions to make sense about excellency of this research and going to figure out the word “best” as the description and adjective for this research as presented in section, “1-failed SuperHyperForcing”. The keyword of this research debut in the section “Applications in Cancer’s Neutrosophic Recognition” with two cases and subsections “Case 1: The Initial Steps Toward SuperHyperBipartite as SuperHyperModel” and “Case 2: The Increasing Steps Toward SuperHyperMultipartite as SuperHyperModel”. In the section, “Open Problems”, there are some scrutiny and discernment on what’s done and what’s happened in this research in the terms of “questions” and “problems” to make sense to figure out this research in featured style. The advantages and the limitations of this research alongside about what’s done in this research to make sense and to get sense about what’s figured out are included in the section, “Conclusion and Closing Remarks”.

1.2. Preliminaries

In this subsection, the basic material which is used in this research, is presented. Also, the new ideas and their clarifications are elicited.

Definition 3 

(Neutrosophic Set). (Ref.[14],Definition 2.1,p.87).

Let X be a space of points (objects) with generic elements in X denoted by $x;$ then the neutrosophic set A (NS A) is an object having the form

$$A=\{<x:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)>,x\in X\}$$

where the functions ${T,I,F:X\to ]}^{-}0,1^{+}[$ define respectively the a truth-membership function, an indeterminacy-membership function, and a falsity-membership function of the element $x\in X$ to the set A with the condition

$${ }^{-}0\le T_A\left(x\right)+I_A\left(x\right)+F_A\left(x\right)\le 3^{+}.$$

The functions $T_A\left(x\right),I_A\left(x\right)$ and $F_A\left(x\right)$ are real standard or nonstandard subsets of ${]}^{-}0,1^{+}[.$

Definition 4 

(Single Valued Neutrosophic Set). (Ref. [17],Definition 6,p.2).

Let X be a space of points (objects) with generic elements in X denoted by $x.$ A single valued neutrosophic set A (SVNS A) is characterized by truth-membership function $T_A\left(x\right),$ an indeterminacy-membership function $I_A\left(x\right),$ and a falsity-membership function $F_A\left(x\right).$ For each point x in $X,$ $T_A\left(x\right), I_A\left(x\right), F_A\left(x\right)\in [0,1].$ A SVNS A can be written as

$$A=\{<x:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)>,x\in X\}.$$

Definition 5. 

The degree of truth-membership, indeterminacy-membership and falsity-membership of the subset $X\subset A$ of the single valued neutrosophic set $A=\{<x:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)>,x\in X\}$:

$$T_A\left(X\right)=min{[T_A\left(v_i\right),T_A\left(v_j\right)]}_{v_i,v_j\in X},$$

$$I_A\left(X\right)=min{[I_A\left(v_i\right),I_A\left(v_j\right)]}_{v_i,v_j\in X},$$

$$\mathrm{and}{F}_A\left(X\right)=min{[F_A\left(v_i\right),F_A\left(v_j\right)]}_{v_i,v_j\in X}.$$

Definition 6. 

The support of $X\subset A$ of the single valued neutrosophic set $A=\{<x:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)>,x\in X\}$:

$$supp\left(X\right)=\{x\in X:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)>0\}.$$

Definition 7 

(Neutrosophic SuperHyperGraph (NSHG)). (Ref.[16],Definition 3,p.291).

Assume $V^{\prime }$ is a given set. A neutrosophic SuperHyperGraph (NSHG) S is an ordered pair $S=(V,E),$ where

(i)

$V=\{V_1,V_2,\dots ,V_n\}$ a finite set of finite single valued neutrosophic subsets of $V^{\prime };$

(ii)

$V=\{(V_i,T_{V^{\prime }}\left(V_i\right),I_{V^{\prime }}\left(V_i\right),F_{V^{\prime }}\left(V_i\right)):T_{V^{\prime }}\left(V_i\right),I_{V^{\prime }}\left(V_i\right),F_{V^{\prime }}\left(V_i\right)\ge 0\},(i=1,2,\dots ,n);$

(iii)

$E=\{E_1,E_2,\dots ,E_{n^{\prime }}\}$ a finite set of finite single valued neutrosophic subsets of $V;$

(iv)

$E=\{(E_{i^{\prime }},T_V^{\prime }\left(E_{i^{\prime }}\right),I_V^{\prime }\left(E_{i^{\prime }}\right),F_V^{\prime }\left(E_{i^{\prime }}\right)):T_V^{\prime }\left(E_{i^{\prime }}\right),I_V^{\prime }\left(E_{i^{\prime }}\right),F_V^{\prime }\left(E_{i^{\prime }}\right)\ge 0\},(i^{\prime }=1,2,\dots ,n^{\prime });$

(v)

$V_i\ne \varnothing ,(i=1,2,\dots ,n);$

(vi)

$E_{i^{\prime }}\ne \varnothing ,(i^{\prime }=1,2,\dots ,n^{\prime });$

(vii)

${\sum }_{i}supp\left(V_i\right)=V,(i=1,2,\dots ,n);$

(viii)

${\sum }_{i^{\prime }}supp\left(E_{i^{\prime }}\right)=V,(i^{\prime }=1,2,\dots ,n^{\prime });$

(ix)

and the following conditions hold:

$$T_V^{\prime }\left(E_{i^{\prime }}\right)\le min{[T_{V^{\prime }}\left(V_i\right),T_{V^{\prime }}\left(V_j\right)]}_{V_i,V_j\in E_{i^{\prime }}},$$

$$I_V^{\prime }\left(E_{i^{\prime }}\right)\le min{[I_{V^{\prime }}\left(V_i\right),I_{V^{\prime }}\left(V_j\right)]}_{V_i,V_j\in E_{i^{\prime }}},$$

$$\mathrm{and}{F}_V^{\prime }\left(E_{i^{\prime }}\right)\le min{[F_{V^{\prime }}\left(V_i\right),F_{V^{\prime }}\left(V_j\right)]}_{V_i,V_j\in E_{i^{\prime }}}$$

where $i^{\prime }=1,2,\dots ,n^{\prime }.$

Here the neutrosophic SuperHyperEdges (NSHE) $E_{j^{\prime }}$ and the neutrosophic SuperHyperVertices (NSHV) $V_j$ are single valued neutrosophic sets. $T_{V^{\prime }}\left(V_i\right),I_{V^{\prime }}\left(V_i\right),$ and $F_{V^{\prime }}\left(V_i\right)$ denote the degree of truth-membership, the degree of indeterminacy-membership and the degree of falsity-membership the neutrosophic SuperHyperVertex (NSHV) $V_i$ to the neutrosophic SuperHyperVertex (NSHV) $V.$$T_V^{\prime }\left(E_{i^{\prime }}\right),T_V^{\prime }\left(E_{i^{\prime }}\right),$ and $T_V^{\prime }\left(E_{i^{\prime }}\right)$ denote the degree of truth-membership, the degree of indeterminacy-membership and the degree of falsity-membership of the neutrosophic SuperHyperEdge (NSHE) $E_{i^{\prime }}$ to the neutrosophic SuperHyperEdge (NSHE) $E.$ Thus, the $i{i}^{\prime }$th element of the incidence matrix of neutrosophic SuperHyperGraph (NSHG) are of the form $(V_i,T_V^{\prime }\left(E_{i^{\prime }}\right),I_V^{\prime }\left(E_{i^{\prime }}\right),F_V^{\prime }\left(E_{i^{\prime }}\right))$, the sets V and E are crisp sets.

Definition 8 

(Characterization of the Neutrosophic SuperHyperGraph (NSHG)). (Ref.[16],Section 4,pp.291-292).

Assume a neutrosophic SuperHyperGraph (NSHG) S is an ordered pair $S=(V,E).$ The neutrosophic SuperHyperEdges (NSHE) $E_{i^{\prime }}$ and the neutrosophic SuperHyperVertices (NSHV) $V_i$ of neutrosophic SuperHyperGraph (NSHG) $S=(V,E)$ could be characterized as follow-up items.

$\left(i\right)$

If $|V_i|=1,$ then $V_i$ is called vertex;

$\left(ii\right)$

if $|V_i|\ge 1,$ then $V_i$ is called SuperVertex;

$\left(iii\right)$

if for all $V_i$s are incident in $E_{i^{\prime }},$$|V_i|=1,$ and $|E_{i^{\prime }}|=2,$ then $E_{i^{\prime }}$ is called edge;

$\left(iv\right)$

if for all $V_i$s are incident in $E_{i^{\prime }},$$|V_i|=1,$ and $|E_{i^{\prime }}|\ge 2,$ then $E_{i^{\prime }}$ is called HyperEdge;

$\left(v\right)$

if there’s a $V_i$ is incident in $E_{i^{\prime }}$ such that $|V_i|\ge 1,$ and $|E_{i^{\prime }}|=2,$ then $E_{i^{\prime }}$ is called SuperEdge;

$\left(vi\right)$

if there’s a $V_i$ is incident in $E_{i^{\prime }}$ such that $|V_i|\ge 1,$ and $|E_{i^{\prime }}|\ge 2,$ then $E_{i^{\prime }}$ is called SuperHyperEdge.

If we choose different types of binary operations, then we could get hugely diverse types of general forms of neutrosophic SuperHyperGraph (NSHG).

Definition 9 

(t-norm). (Ref.[15], Definition 5.1.1, pp.82-83).

A binary operation $\otimes :[0,1]\times [0,1]\to [0,1]$ is a t-norm if it satisfies the following for $x,y,z,w\in [0,1]$:

$\left(i\right)$

$1\otimes x=x;$

$\left(ii\right)$

$x\otimes y=y\otimes x;$

$\left(iii\right)$

$x\otimes (y\otimes z)=(x\otimes y)\otimes z;$

$\left(iv\right)$

If $w\le x$ and $y\le z$ then $w\otimes y\le x\otimes z.$

Definition 10. 

The degree of truth-membership, indeterminacy-membership and falsity-membership of the subset $X\subset A$ of the single valued neutrosophic set $A=\{<x:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)>,x\in X\}$ (with respect to t-norm $T_{norm}$):

$$T_A\left(X\right)=T_{norm}{[T_A\left(v_i\right),T_A\left(v_j\right)]}_{v_i,v_j\in X},$$

$$I_A\left(X\right)=T_{norm}{[I_A\left(v_i\right),I_A\left(v_j\right)]}_{v_i,v_j\in X},$$

$$\mathrm{and}{F}_A\left(X\right)=T_{norm}{[F_A\left(v_i\right),F_A\left(v_j\right)]}_{v_i,v_j\in X}.$$

Definition 11. 

The support of $X\subset A$ of the single valued neutrosophic set $A=\{<x:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)>,x\in X\}$:

$$supp\left(X\right)=\{x\in X:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)>0\}.$$

Definition 12. 

(General Forms of Neutrosophic SuperHyperGraph (NSHG)).

Assume $V^{\prime }$ is a given set. A neutrosophic SuperHyperGraph (NSHG) S is an ordered pair $S=(V,E),$ where

$\left(i\right)$

$V=\{V_1,V_2,\dots ,V_n\}$ a finite set of finite single valued neutrosophic subsets of $V^{\prime };$

$\left(ii\right)$

$V=\{(V_i,T_{V^{\prime }}\left(V_i\right),I_{V^{\prime }}\left(V_i\right),F_{V^{\prime }}\left(V_i\right)):T_{V^{\prime }}\left(V_i\right),I_{V^{\prime }}\left(V_i\right),F_{V^{\prime }}\left(V_i\right)\ge 0\},(i=1,2,\dots ,n);$

$\left(iii\right)$

$E=\{E_1,E_2,\dots ,E_{n^{\prime }}\}$ a finite set of finite single valued neutrosophic subsets of $V;$

$\left(iv\right)$

$E=\{(E_{i^{\prime }},T_V^{\prime }\left(E_{i^{\prime }}\right),I_V^{\prime }\left(E_{i^{\prime }}\right),F_V^{\prime }\left(E_{i^{\prime }}\right)):T_V^{\prime }\left(E_{i^{\prime }}\right),I_V^{\prime }\left(E_{i^{\prime }}\right),F_V^{\prime }\left(E_{i^{\prime }}\right)\ge 0\},(i^{\prime }=1,2,\dots ,n^{\prime });$

$\left(v\right)$

$V_i\ne \varnothing ,(i=1,2,\dots ,n);$

$\left(vi\right)$

$E_{i^{\prime }}\ne \varnothing ,(i^{\prime }=1,2,\dots ,n^{\prime });$

$\left(vii\right)$

${\sum }_{i}supp\left(V_i\right)=V,(i=1,2,\dots ,n);$

$\left(viii\right)$

${\sum }_{i^{\prime }}supp\left(E_{i^{\prime }}\right)=V,(i^{\prime }=1,2,\dots ,n^{\prime }).$

Here the neutrosophic SuperHyperEdges (NSHE) $E_{j^{\prime }}$ and the neutrosophic SuperHyperVertices (NSHV) $V_j$ are single valued neutrosophic sets. $T_{V^{\prime }}\left(V_i\right),I_{V^{\prime }}\left(V_i\right),$ and $F_{V^{\prime }}\left(V_i\right)$ denote the degree of truth-membership, the degree of indeterminacy-membership and the degree of falsity-membership the neutrosophic SuperHyperVertex (NSHV) $V_i$ to the neutrosophic SuperHyperVertex (NSHV) $V.$$T_V^{\prime }\left(E_{i^{\prime }}\right),T_V^{\prime }\left(E_{i^{\prime }}\right),$ and $T_V^{\prime }\left(E_{i^{\prime }}\right)$ denote the degree of truth-membership, the degree of indeterminacy-membership and the degree of falsity-membership of the neutrosophic SuperHyperEdge (NSHE) $E_{i^{\prime }}$ to the neutrosophic SuperHyperEdge (NSHE) $E.$ Thus, the $i{i}^{\prime }$th element of the incidence matrix of neutrosophic SuperHyperGraph (NSHG) are of the form $(V_i,T_V^{\prime }\left(E_{i^{\prime }}\right),I_V^{\prime }\left(E_{i^{\prime }}\right),F_V^{\prime }\left(E_{i^{\prime }}\right))$, the sets V and E are crisp sets.

Definition 13 

(Characterization of the Neutrosophic SuperHyperGraph (NSHG)). (Ref.[16],Section 4,pp.291-292).

Assume a neutrosophic SuperHyperGraph (NSHG) S is an ordered pair $S=(V,E).$ The neutrosophic SuperHyperEdges (NSHE) $E_{i^{\prime }}$ and the neutrosophic SuperHyperVertices (NSHV) $V_i$ of neutrosophic SuperHyperGraph (NSHG) $S=(V,E)$ could be characterized as follow-up items.

$\left(i\right)$

If $|V_i|=1,$ then $V_i$ is called vertex;

$\left(ii\right)$

if $|V_i|\ge 1,$ then $V_i$ is called SuperVertex;

$\left(iii\right)$

if for all $V_i$s are incident in $E_{i^{\prime }},$$|V_i|=1,$ and $|E_{i^{\prime }}|=2,$ then $E_{i^{\prime }}$ is called edge;

$\left(iv\right)$

if for all $V_i$s are incident in $E_{i^{\prime }},$$|V_i|=1,$ and $|E_{i^{\prime }}|\ge 2,$ then $E_{i^{\prime }}$ is called HyperEdge;

$\left(v\right)$

if there’s a $V_i$ is incident in $E_{i^{\prime }}$ such that $|V_i|\ge 1,$ and $|E_{i^{\prime }}|=2,$ then $E_{i^{\prime }}$ is called SuperEdge;

$\left(vi\right)$

if there’s a $V_i$ is incident in $E_{i^{\prime }}$ such that $|V_i|\ge 1,$ and $|E_{i^{\prime }}|\ge 2,$ then $E_{i^{\prime }}$ is called SuperHyperEdge.

This SuperHyperModel is too messy and too dense. Thus there’s a need to have some restrictions and conditions on SuperHyperGraph. The special case of this SuperHyperGraph makes the patterns and regularities.

Definition 14. 

A graph is SuperHyperUniform if it’s SuperHyperGraph and the number of elements of SuperHyperEdges are the same.

To get more visions on 1-failed SuperHyperForcing, the some SuperHyperClasses are introduced. It makes to have 1-failed SuperHyperForcing more understandable.

Definition 15. 

Assume a neutrosophic SuperHyperGraph. There are some SuperHyperClasses as follows.

(i).

It’s SuperHyperPath if it’s only one SuperVertex as intersection amid two given SuperHyperEdges with two exceptions;

(ii).

it’s SuperHyperCycle if it’s only one SuperVertex as intersection amid two given SuperHyperEdges;

(iii).

it’s SuperHyperStar it’s only one SuperVertex as intersection amid all SuperHyperEdges;

(iv).

it’s SuperHyperBipartite it’s only one SuperVertex as intersection amid two given SuperHyperEdges and these SuperVertices, forming two separate sets, has no SuperHyperEdge in common;

(v).

it’s SuperHyperMultiPartite it’s only one SuperVertex as intersection amid two given SuperHyperEdges and these SuperVertices, forming multi separate sets, has no SuperHyperEdge in common;

(vi).

it’s SuperHyperWheel if it’s only one SuperVertex as intersection amid two given SuperHyperEdges and one SuperVertex has one SuperHyperEdge with any common SuperVertex.

Definition 16. 

Let an ordered pair $S=(V,E)$ be a neutrosophic SuperHyperGraph (NSHG) $S.$ Then a sequence of neutrosophic SuperHyperVertices (NSHV) and neutrosophic SuperHyperEdges (NSHE)

$$V_1,E_1,V_2,E_2,V_3,\dots ,V_{s-1},E_{s-1},V_s$$

is called a neutrosophic SuperHyperPath (NSHP) from neutrosophic SuperHyperVertex (NSHV) $V_1$ to neutrosophic SuperHyperVertex (NSHV) $V_s$ if either of following conditions hold:

$\left(i\right)$

$V_i,V_{i+1}\in E_{i^{\prime }};$

$\left(ii\right)$

there’s a vertex $v_i\in V_i$ such that $v_i,V_{i+1}\in E_{i^{\prime }};$

$\left(iii\right)$

there’s a SuperVertex $V_i^{\prime }\in V_i$ such that $V_i^{\prime },V_{i+1}\in E_{i^{\prime }};$

$\left(iv\right)$

there’s a vertex $v_{i+1}\in V_{i+1}$ such that $V_i,v_{i+1}\in E_{i^{\prime }};$

$\left(v\right)$

there’s a SuperVertex $V_{i+1}^{\prime }\in V_{i+1}$ such that $V_i,V_{i+1}^{\prime }\in E_{i^{\prime }};$

$\left(vi\right)$

there are a vertex $v_i\in V_i$ and a vertex $v_{i+1}\in V_{i+1}$ such that $v_i,v_{i+1}\in E_{i^{\prime }};$

$\left(vii\right)$

there are a vertex $v_i\in V_i$ and a SuperVertex $V_{i+1}^{\prime }\in V_{i+1}$ such that $v_i,V_{i+1}^{\prime }\in E_{i^{\prime }};$

$\left(viii\right)$

there are a SuperVertex $V_i^{\prime }\in V_i$ and a vertex $v_{i+1}\in V_{i+1}$ such that $V_i^{\prime },v_{i+1}\in E_{i^{\prime }};$

$\left(ix\right)$

there are a SuperVertex $V_i^{\prime }\in V_i$ and a SuperVertex $V_{i+1}^{\prime }\in V_{i+1}$ such that $V_i^{\prime },V_{i+1}^{\prime }\in E_{i^{\prime }}.$

Definition 17. 

(Characterization of the Neutrosophic SuperHyperPaths).

Assume a neutrosophic SuperHyperGraph (NSHG) S is an ordered pair $S=(V,E).$ A neutrosophic SuperHyperPath (NSHP) from neutrosophic SuperHyperVertex (NSHV) $V_1$ to neutrosophic SuperHyperVertex (NSHV) $V_s$ is sequence of neutrosophic SuperHyperVertices (NSHV) and neutrosophic SuperHyperEdges (NSHE)

$$V_1,E_1,V_2,E_2,V_3,\dots ,V_{s-1},E_{s-1},V_s,$$

could be characterized as follow-up items.

$\left(i\right)$

If for all $V_i,E_{j^{\prime }},$$|V_i|=1,|E_{j^{\prime }}|=2,$ then NSHP is called path;

$\left(ii\right)$

if for all $E_{j^{\prime }},$$|E_{j^{\prime }}|=2,$ and there’s $V_i,$$|V_i|\ge 1,$ then NSHP is called SuperPath;

$\left(iii\right)$

if for all $V_i,E_{j^{\prime }},$$|V_i|=1,|E_{j^{\prime }}|\ge 2,$ then NSHP is called HyperPath;

$\left(iv\right)$

if there are $V_i,E_{j^{\prime }},$$|V_i|\ge 1,|E_{j^{\prime }}|\ge 2,$ then NSHP is called SuperHyperPath.

Definition 18. 

((neutrosophic) 1-failed SuperHyperForcing).

Assume a SuperHyperGraph. Then

$\left(i\right)$

a 1-failed SuperHyperForcing $\mathcal{Z}\left(NSHG\right)$ for a neutrosophic SuperHyperGraph $NSHG:(V,E)$ is the maximum cardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. The additional condition is referred by “1-” about the usage of any black SuperHyperVertex only once to act on white SuperHyperVertex to be black SuperHyperVertex;

$\left(ii\right)$

a neutrosophic 1-failed SuperHyperForcing ${\mathcal{Z}}_n\left(NSHG\right)$ for a neutrosophic SuperHyperGraph $NSHG:(V,E)$ is the maximum neutrosophic cardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. The additional condition is referred by “1-” about the usage of any black SuperHyperVertex only once to act on white SuperHyperVertex to be black SuperHyperVertex.

Definition 19. 

((neutrosophic)$\delta -$ 1-failed SuperHyperForcing).

Assume a SuperHyperGraph. Then

$\left(i\right)$

a $\mathbf{\delta }\mathbf{-}$1-failed SuperHyperForcing is a maximal 1-failed SuperHyperForcing of SuperHyperVertices with maximum cardinality such that either of the following expressions hold for the (neutrosophic) cardinalities of SuperHyperNeighbors of $s\in S:$

$$\begin{array}{ccc}& & |S\cap N(s\left)\right|>|S\cap (V\setminus N\left(s\right)\left)\right|+\delta ;\hfill \end{array}$$

(1.1)

$$\begin{array}{ccc}& & |S\cap N(s\left)\right|<|S\cap (V\setminus N\left(s\right)\left)\right|+\delta .\hfill \end{array}$$

(1.2)

The Expression (1.1), holds if S is an $\delta -$SuperHyperOffensive. And the Expression (1.2), holds if S is an $\delta -$SuperHyperDefensive;

$\left(ii\right)$

a neutrosophic $\mathbf{\delta }\mathbf{-}$1-failed SuperHyperForcing is a maximal neutrosophic 1-failed SuperHyperForcing of SuperHyperVertices with maximum neutrosophic cardinality such that either of the following expressions hold for the neutrosophic cardinalities of SuperHyperNeighbors of $s\in S:$

$$\begin{array}{ccc}& & {|S\cap N\left(s\right)|}_{neutrosophic}>{|S\cap (V\setminus N\left(s\right))|}_{neutrosophic}+\delta ;\hfill \end{array}$$

(1.3)

$$\begin{array}{ccc}& & {|S\cap N\left(s\right)|}_{neutrosophic}<{|S\cap (V\setminus N\left(s\right))|}_{neutrosophic}+\delta .\hfill \end{array}$$

(1.4)

The Expression (1.3), holds if S is a neutrosophic $\delta -$SuperHyperOffensive. And the Expression (1.4), holds if S is a neutrosophic $\delta -$SuperHyperDefensive.

For the sake of having neutrosophic 1-failed SuperHyperForcing, there’s a need to “redefine” the notion of “neutrosophic SuperHyperGraph”. The SuperHyperVertices and the SuperHyperEdges are assigned by the labels from the letters of the alphabets. In this procedure, there’s the usage of the position of labels to assign to the values.

Definition 20. 

Assume a neutrosophic SuperHyperGraph. It’s redefined neutrosophic SuperHyperGraph if the Table (1) holds.

Table 1. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperGraph Mentioned in the Definition (20)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 1. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperGraph Mentioned in the Definition (20)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

It’s useful to define “neutrosophic” version of SuperHyperClasses. Since there’s more ways to get neutrosophic type-results to make neutrosophic 1-failed SuperHyperForcing more understandable.

Definition 21. 

Assume a neutrosophic SuperHyperGraph. There are some neutrosophic SuperHyperClasses if the Table (2) holds. Thus SuperHyperPath, SuperHyperCycle, SuperHyperStar, SuperHyperBipartite, SuperHyperMultiPartite, and SuperHyperWheel, are neutrosophic SuperHyperPath, neutrosophic SuperHyperCycle, neutrosophic SuperHyperStar, neutrosophic SuperHyperBipartite, neutrosophic SuperHyperMultiPartite, and neutrosophic SuperHyperWheel if the Table (2) holds.

Table 2. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperGraph, Mentioned in the Definition (21)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 2. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperGraph, Mentioned in the Definition (21)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

It’s useful to define “neutrosophic” version of 1-failed SuperHyperForcing. Since there’s more ways to get type-results to make 1-failed SuperHyperForcing more understandable.

For the sake of having neutrosophic 1-failed SuperHyperForcing, there’s a need to “redefine” the notion of “1-failed SuperHyperForcing”. The SuperHyperVertices and the SuperHyperEdges are assigned by the labels from the letters of the alphabets. In this procedure, there’s the usage of the position of labels to assign to the values.

Definition 22. 

Assume a 1-failed SuperHyperForcing. It’s redefined neutrosophic 1-failed SuperHyperForcing if the Table (3) holds.

Table 3. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperGraph Mentioned in the Definition (22)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 3. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperGraph Mentioned in the Definition (22)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

2. Neutrosophic 1-Failed SuperHyperForcing

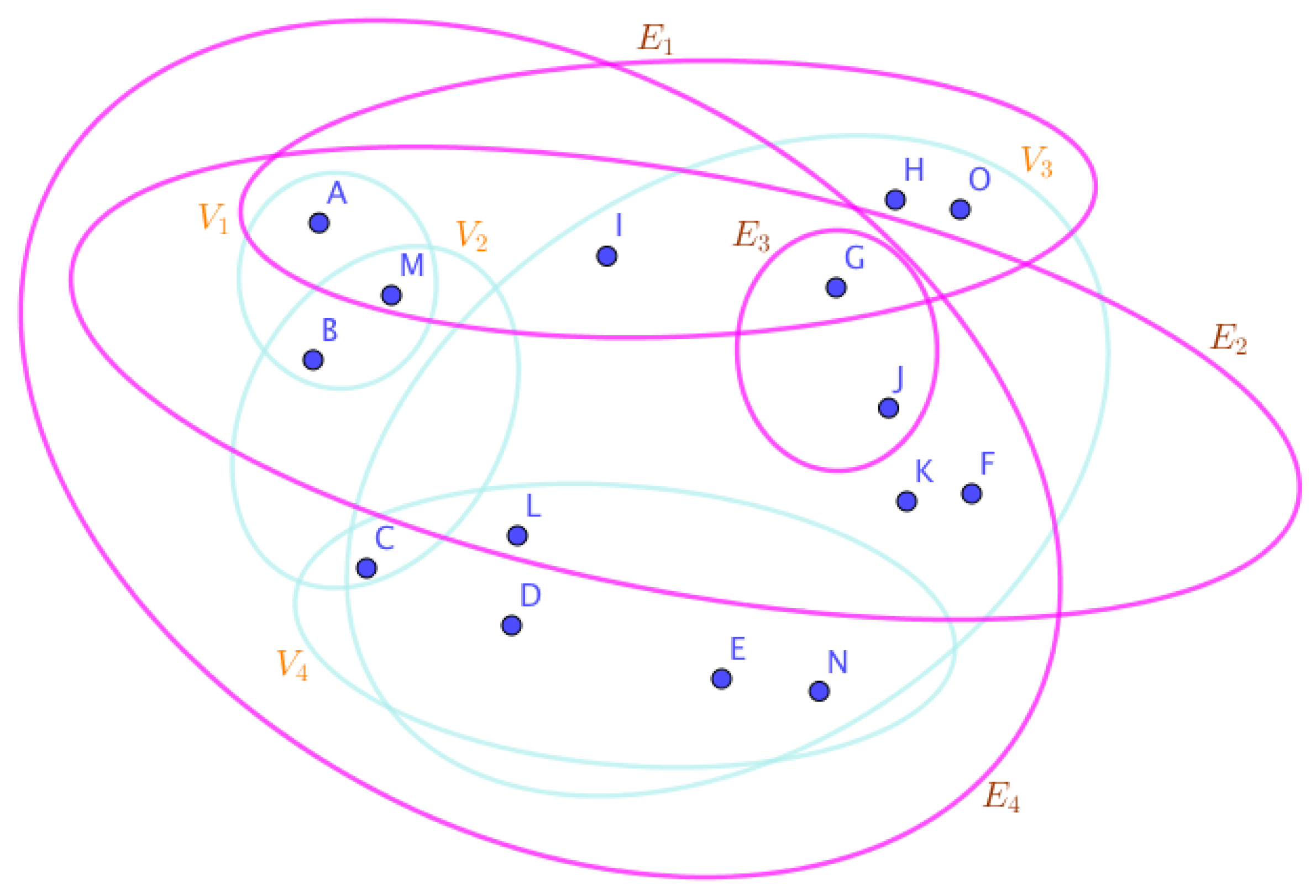
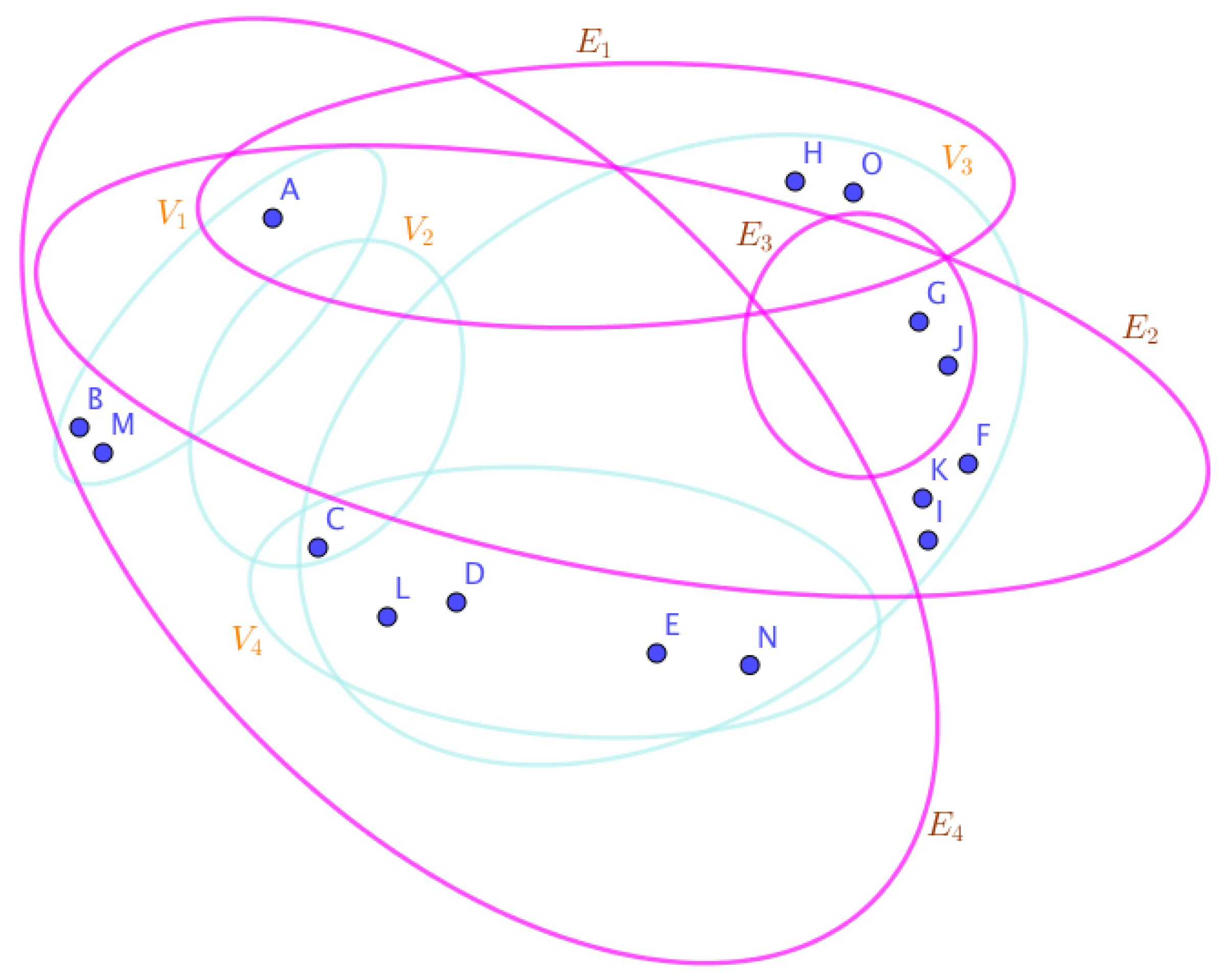
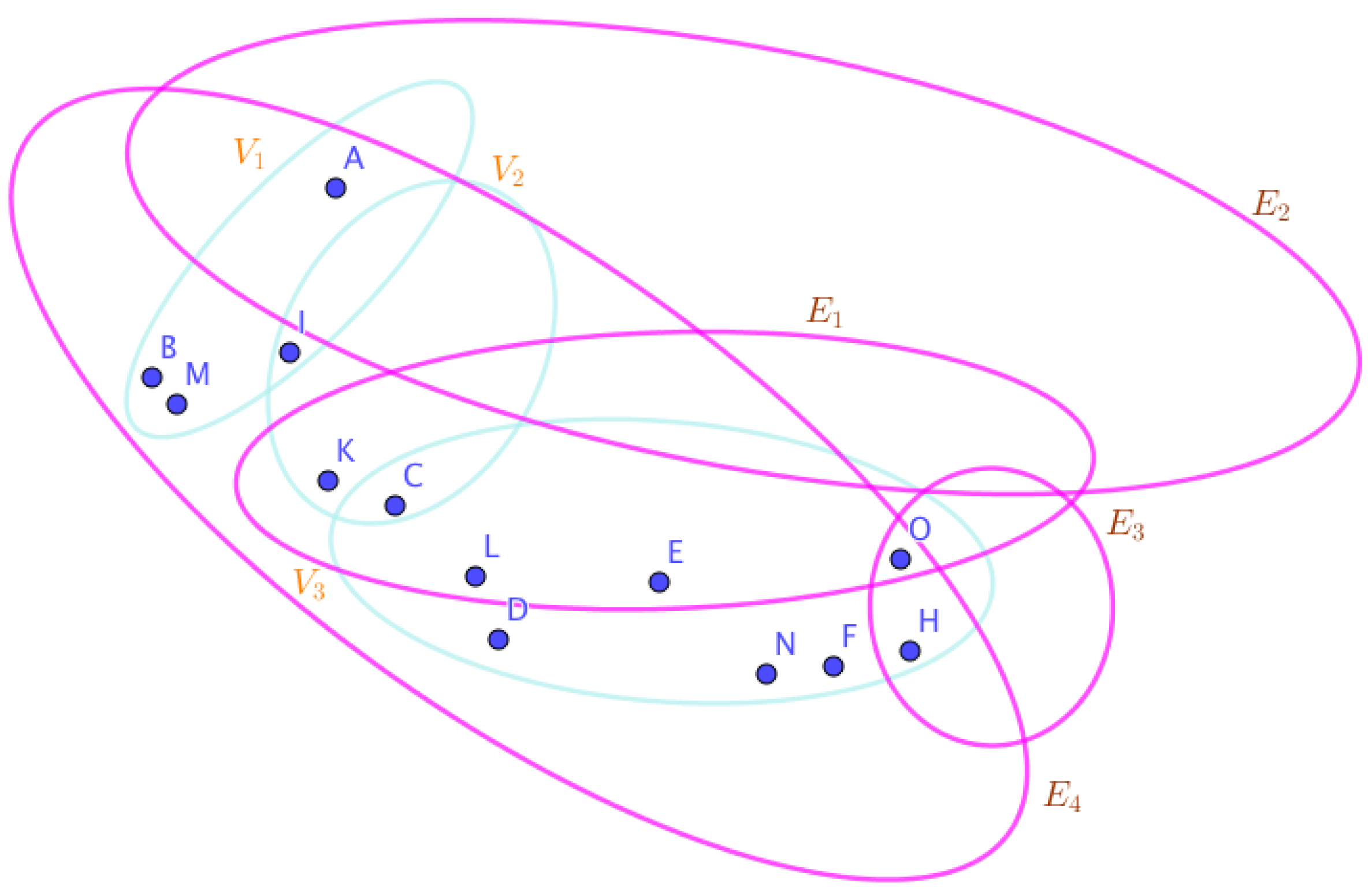
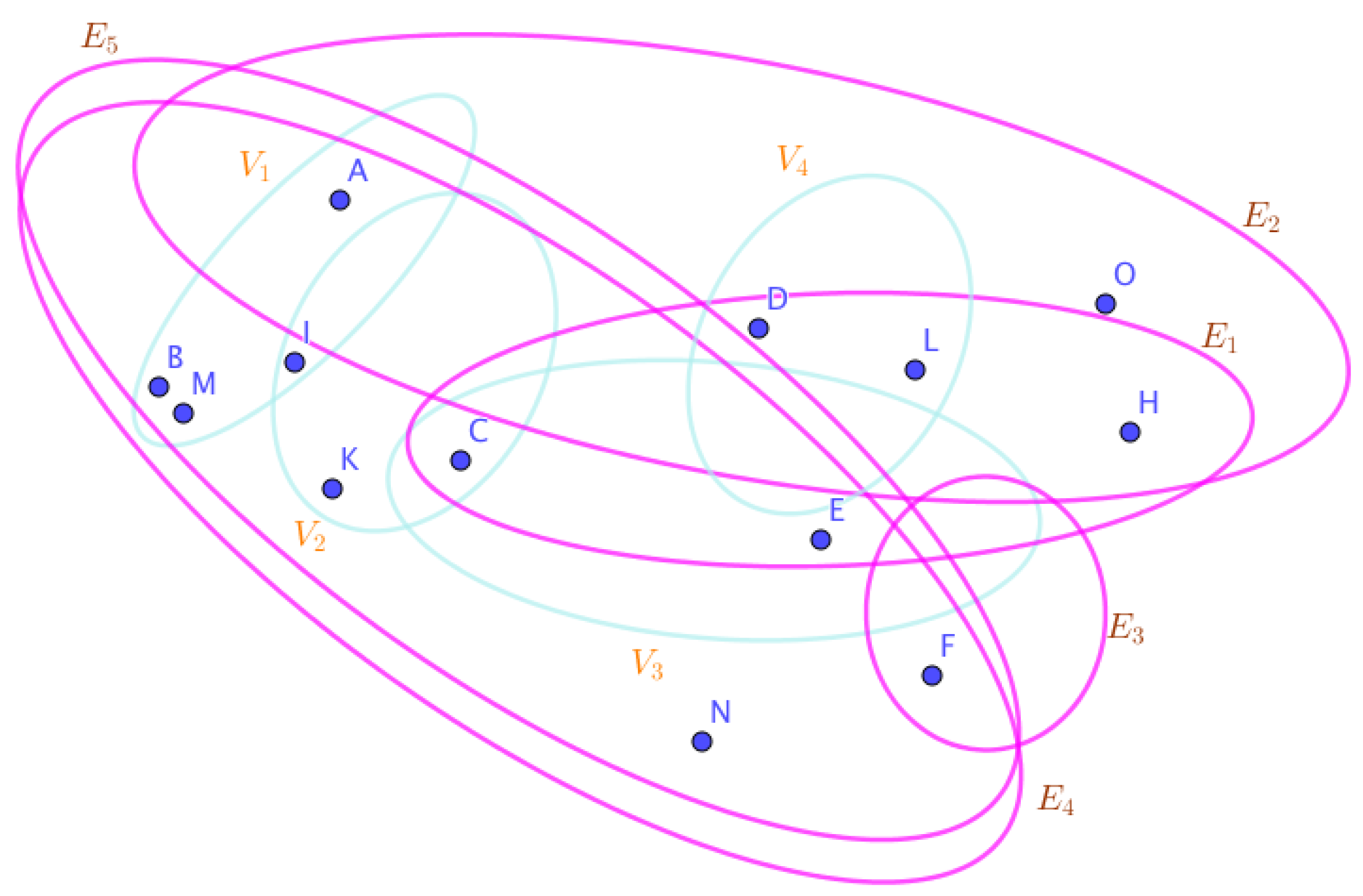
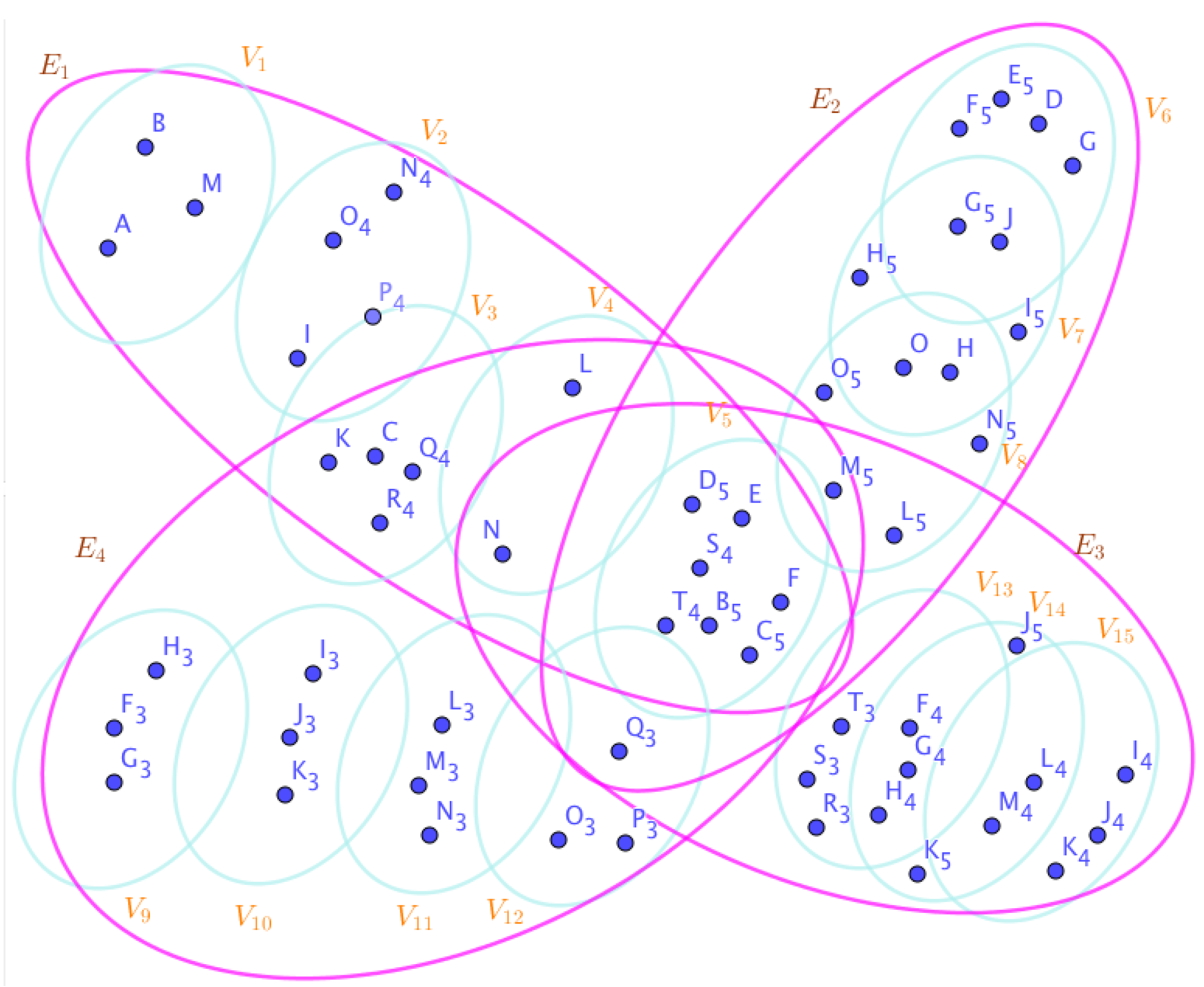
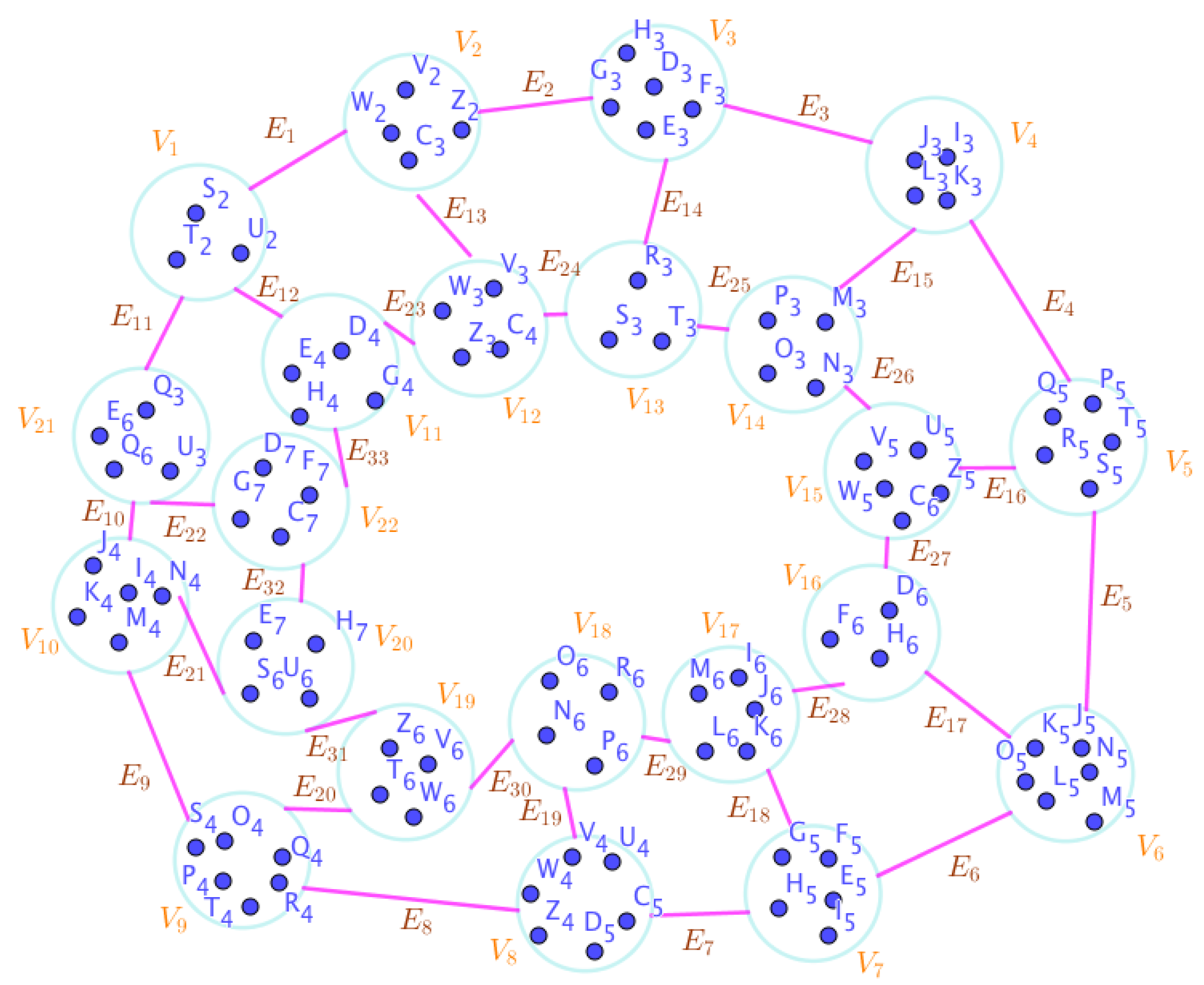
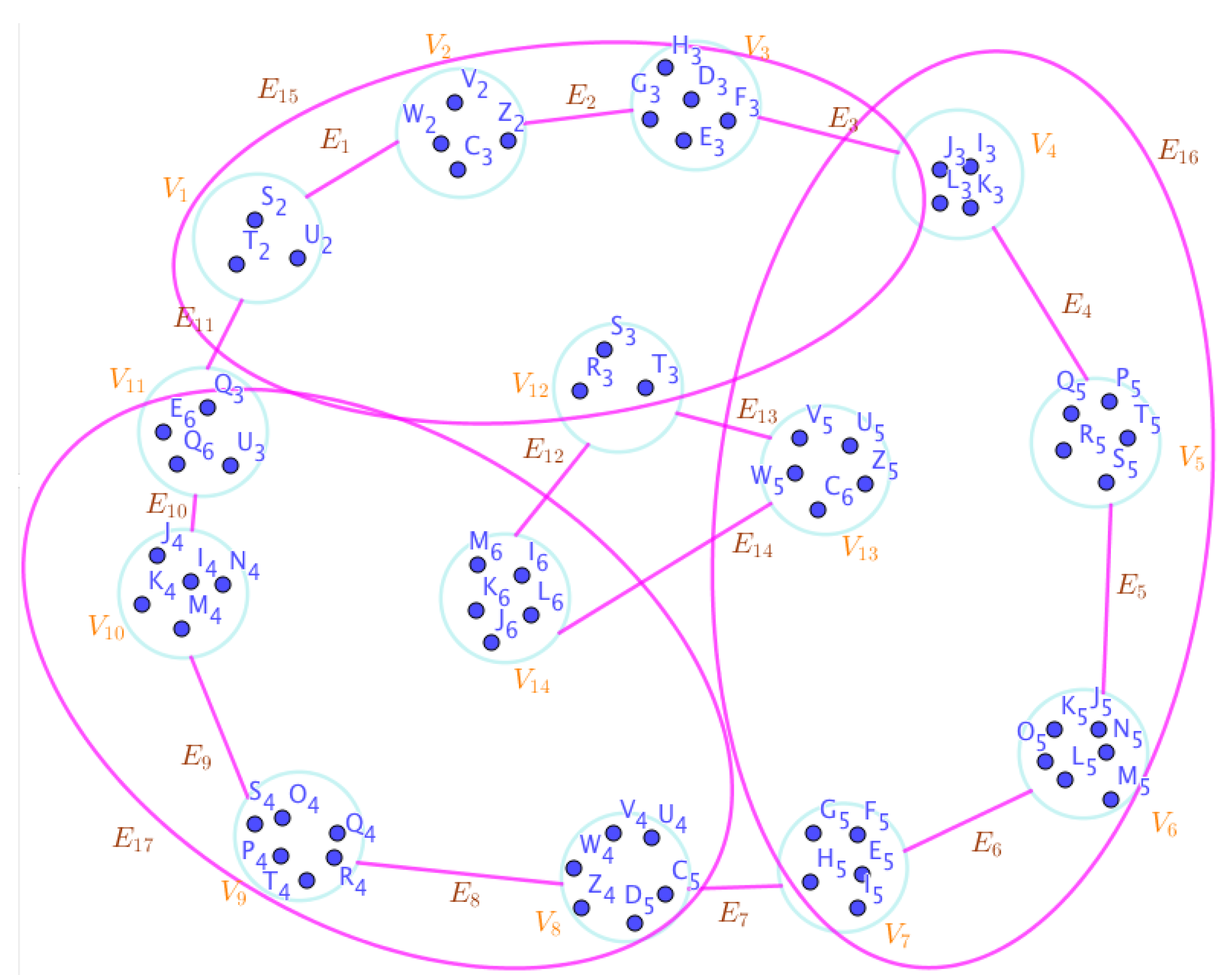
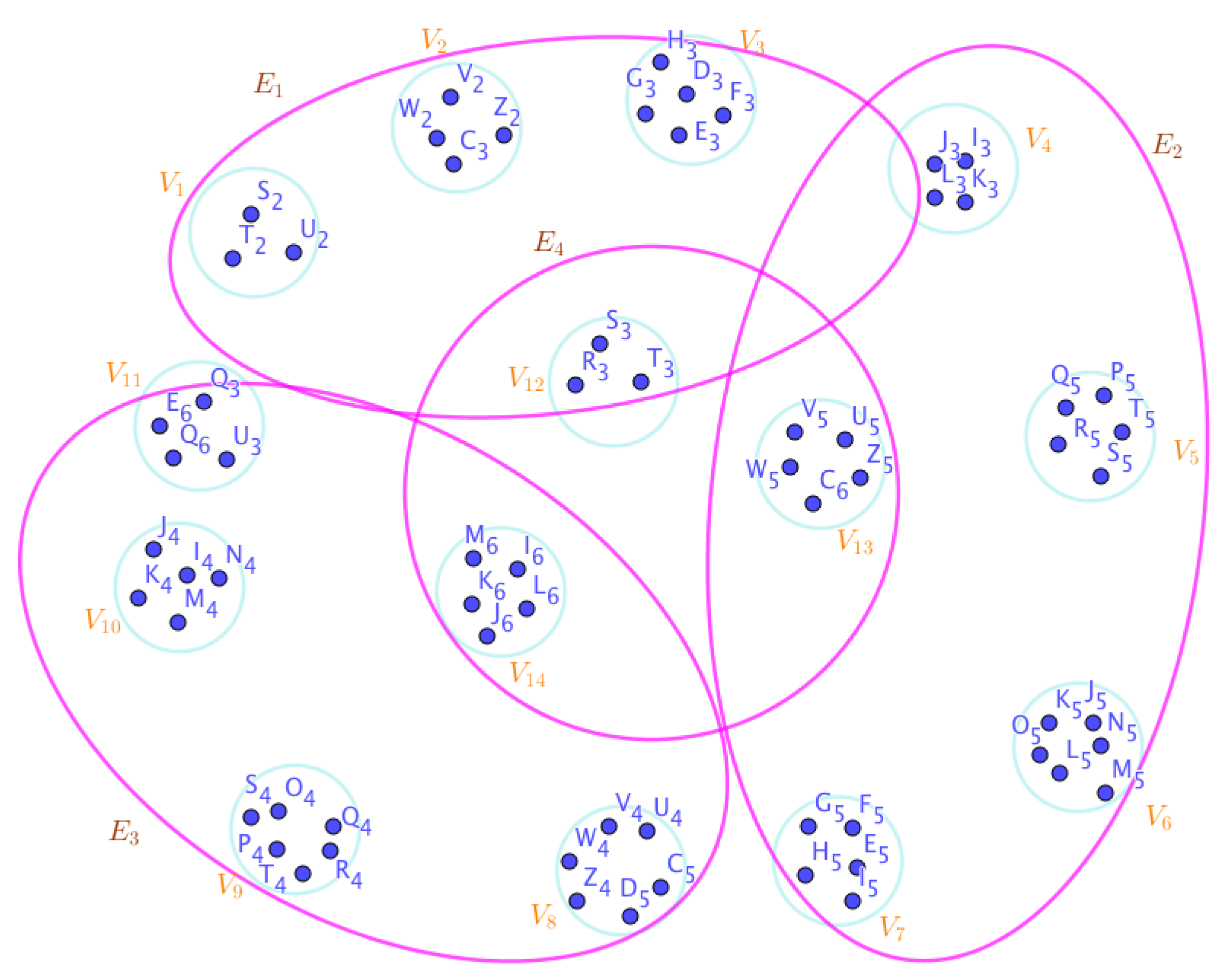
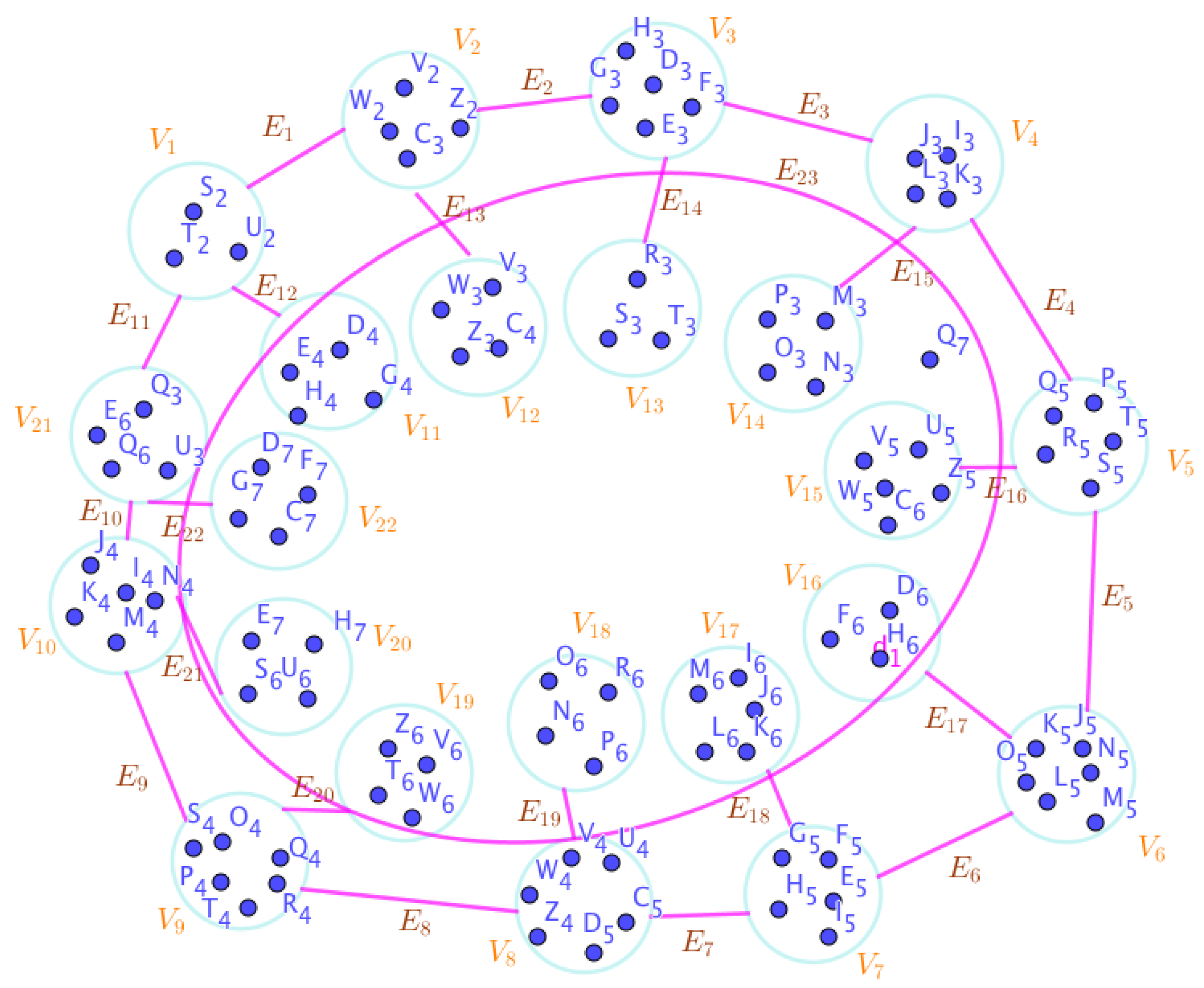
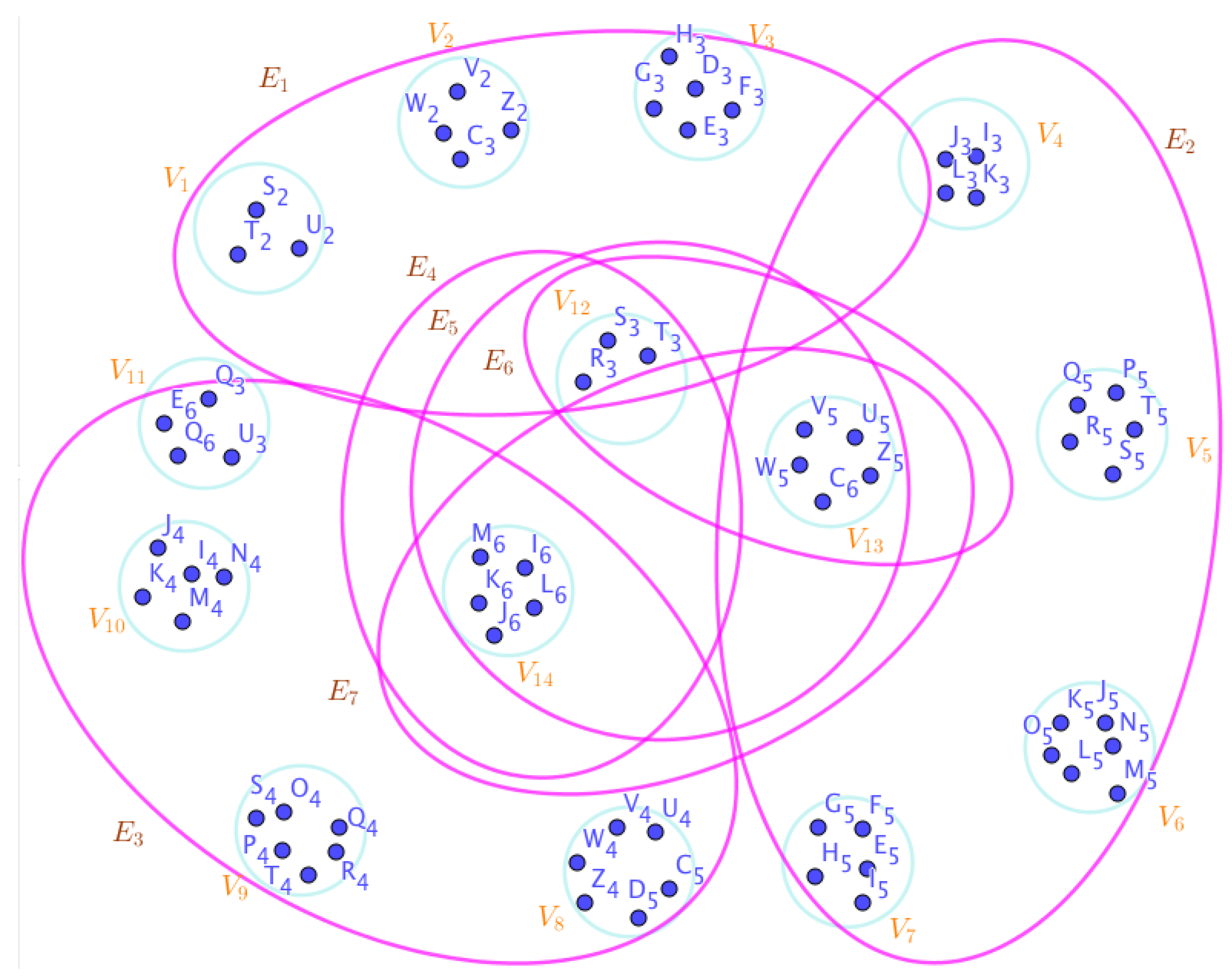
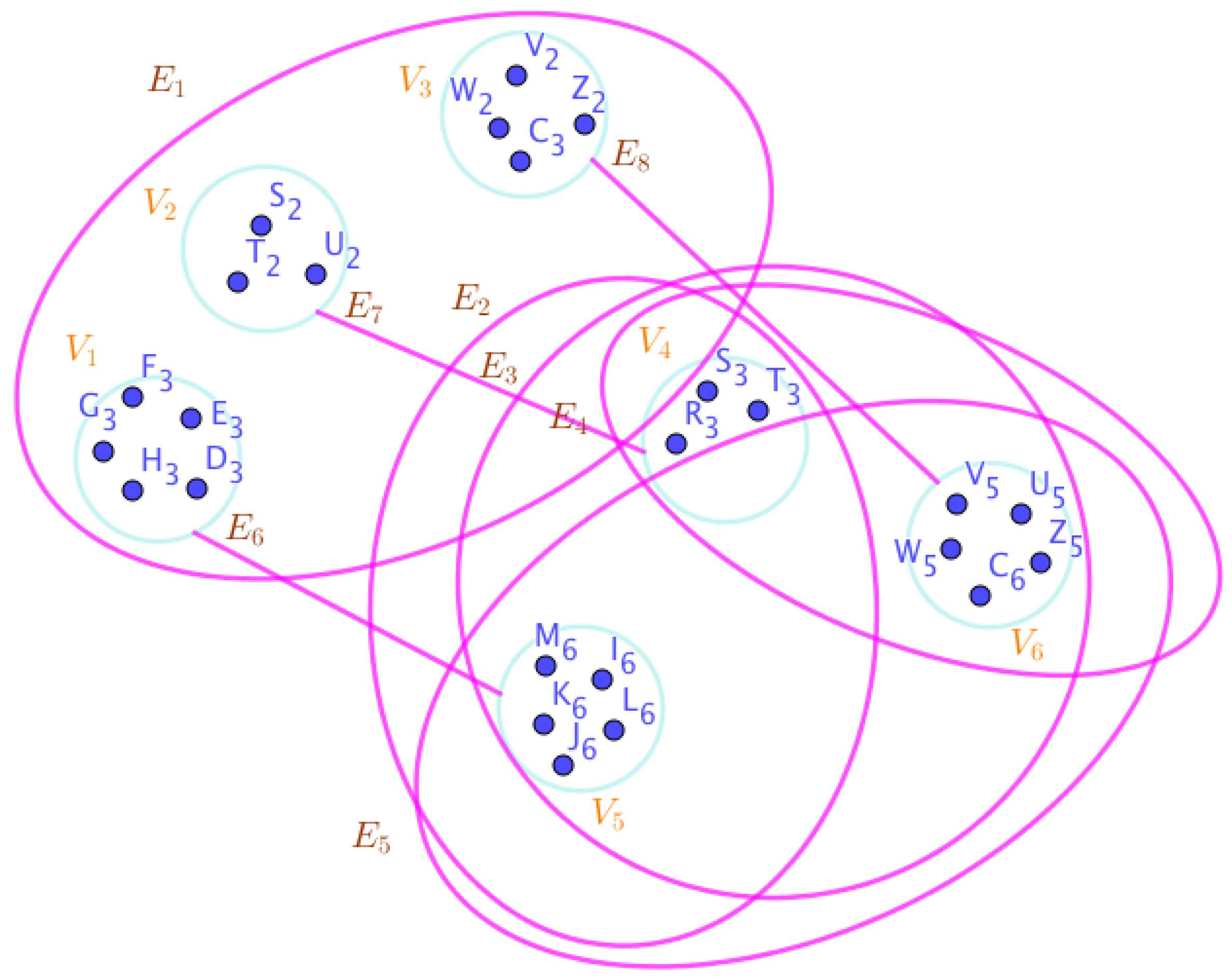
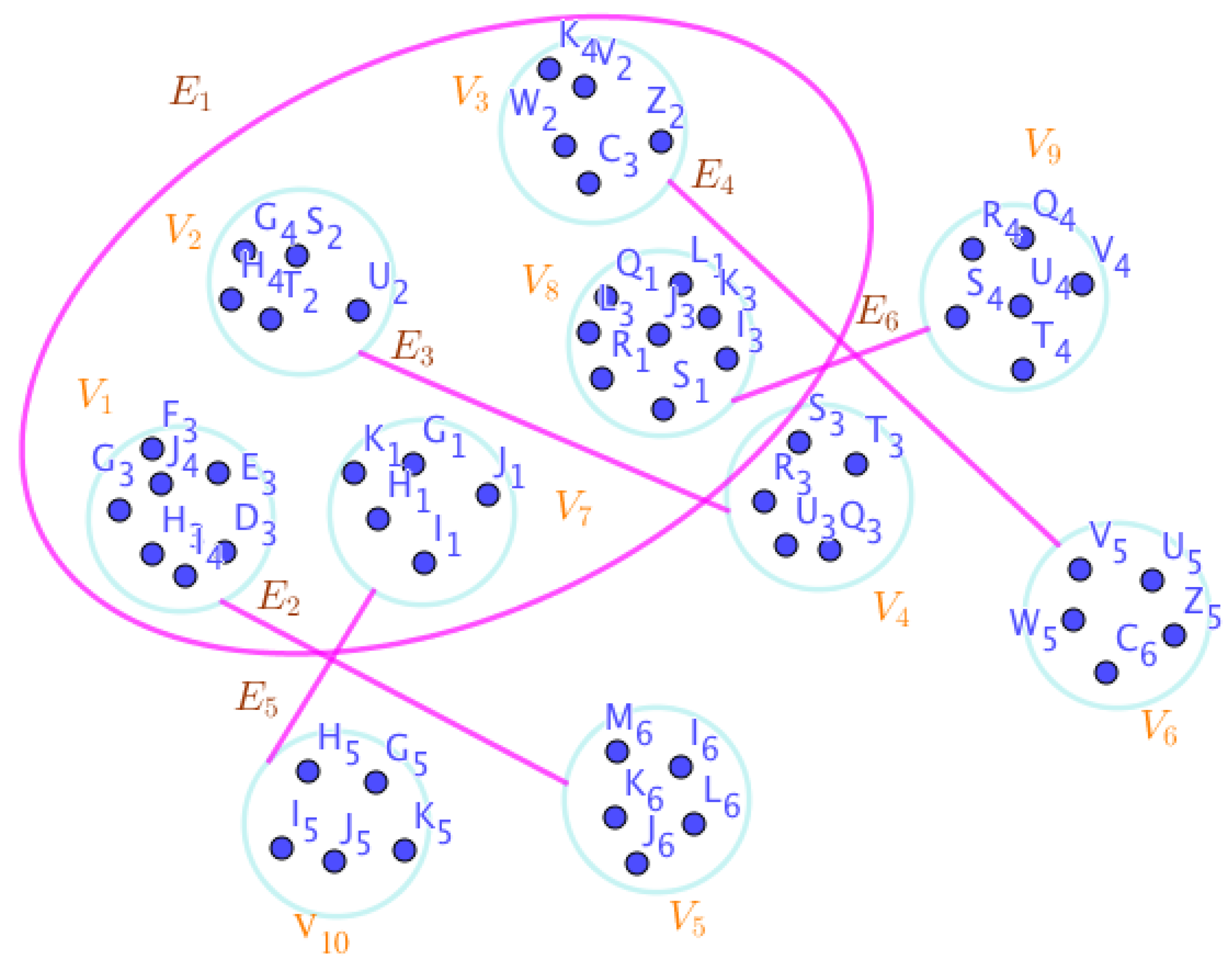
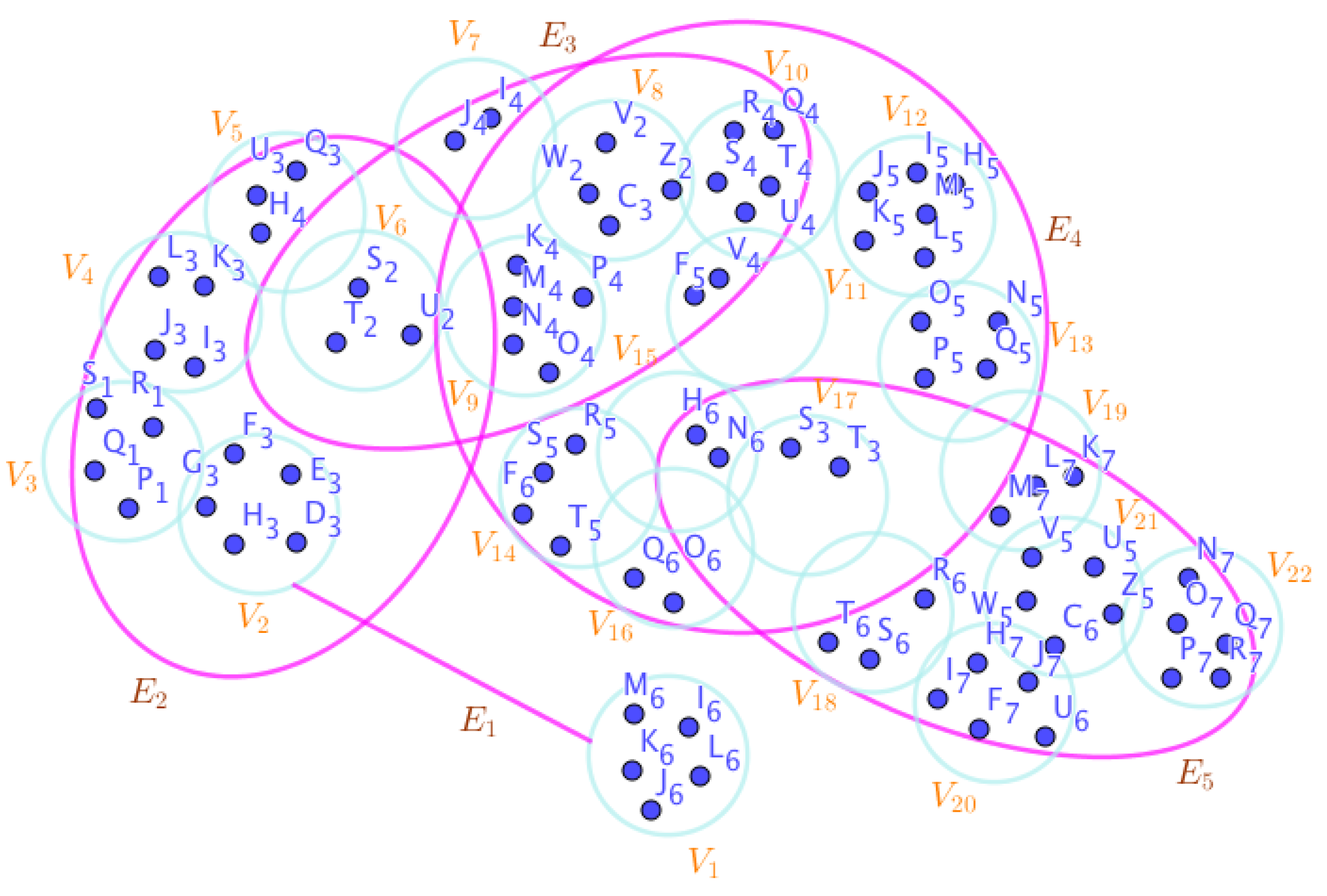
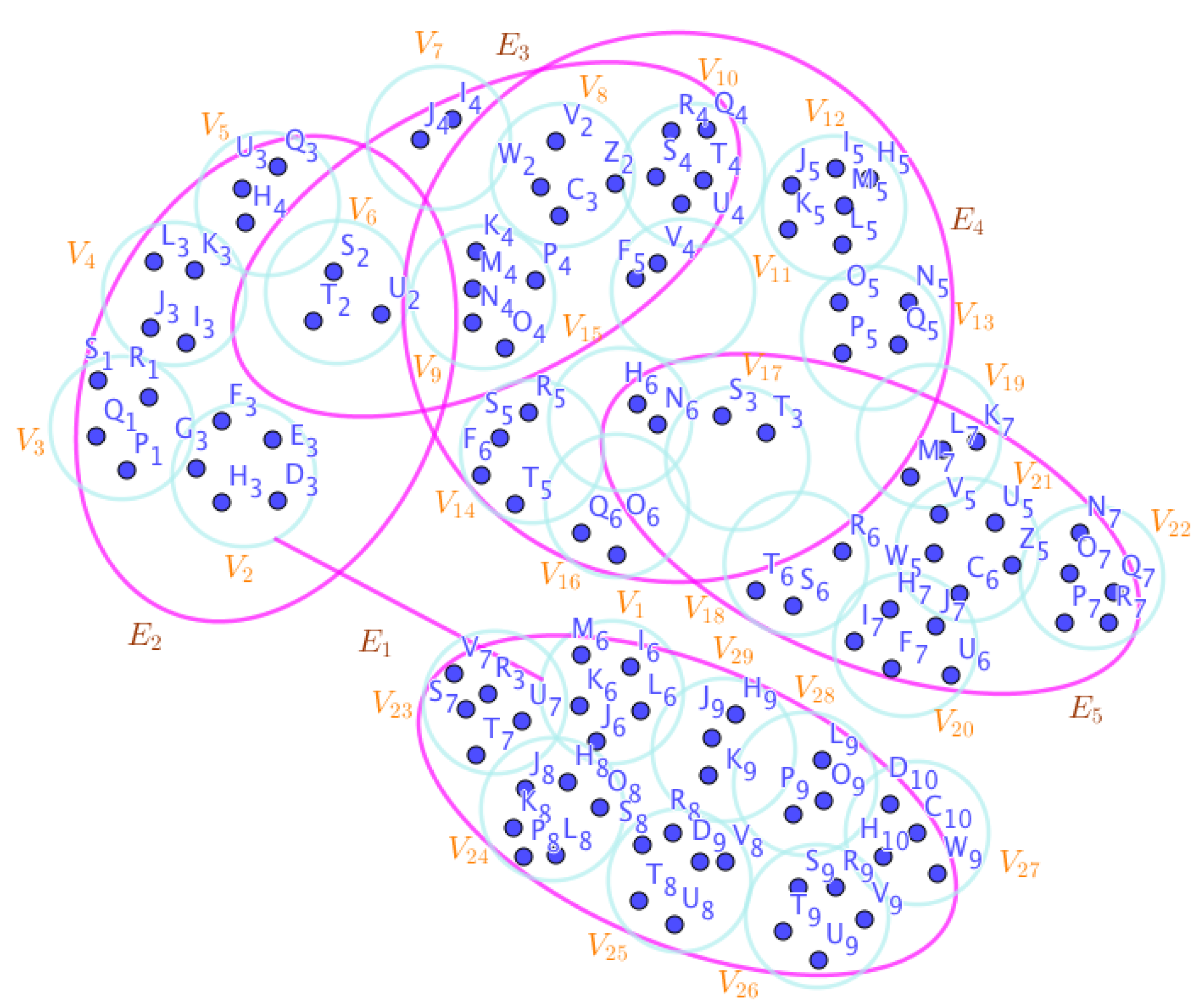
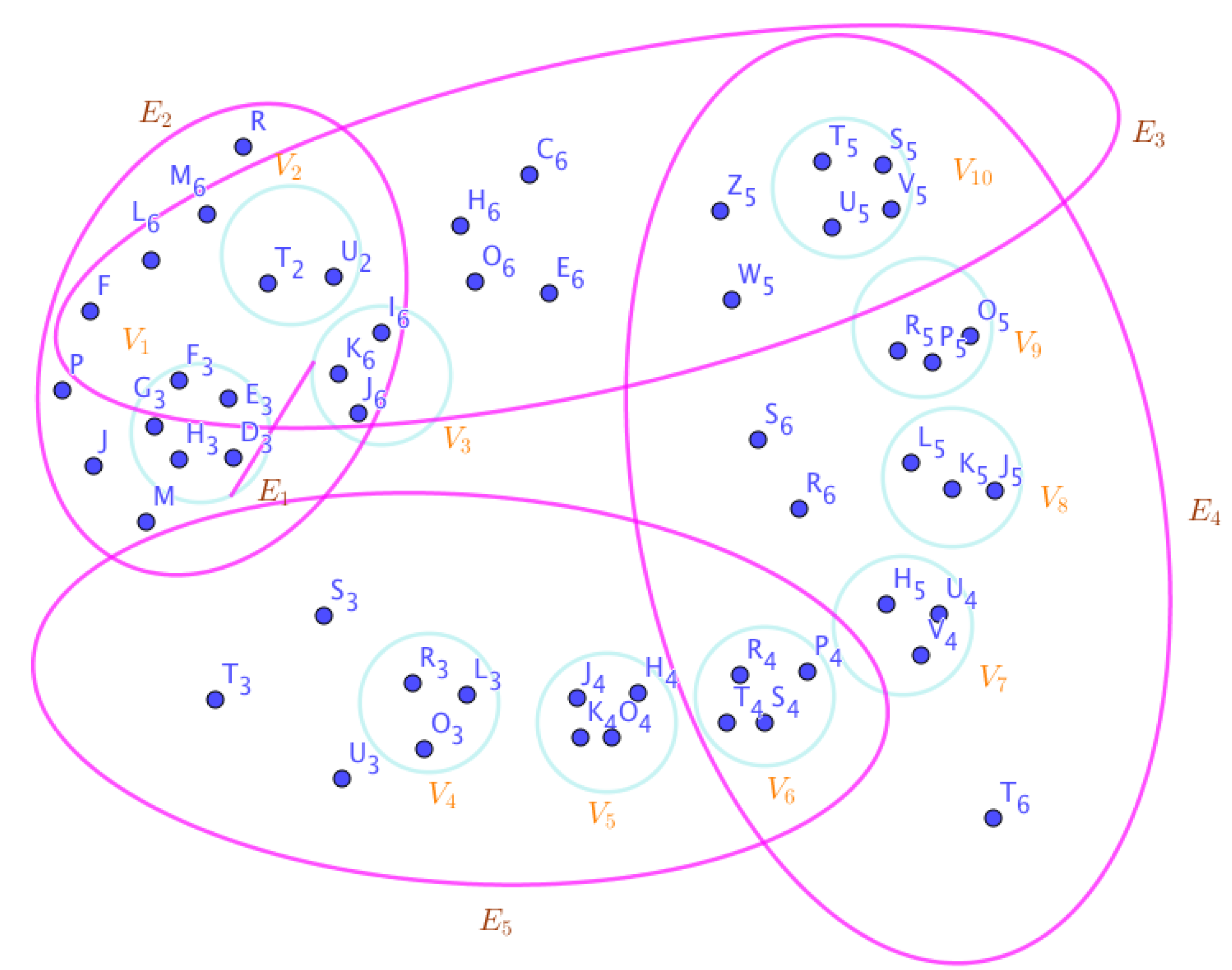
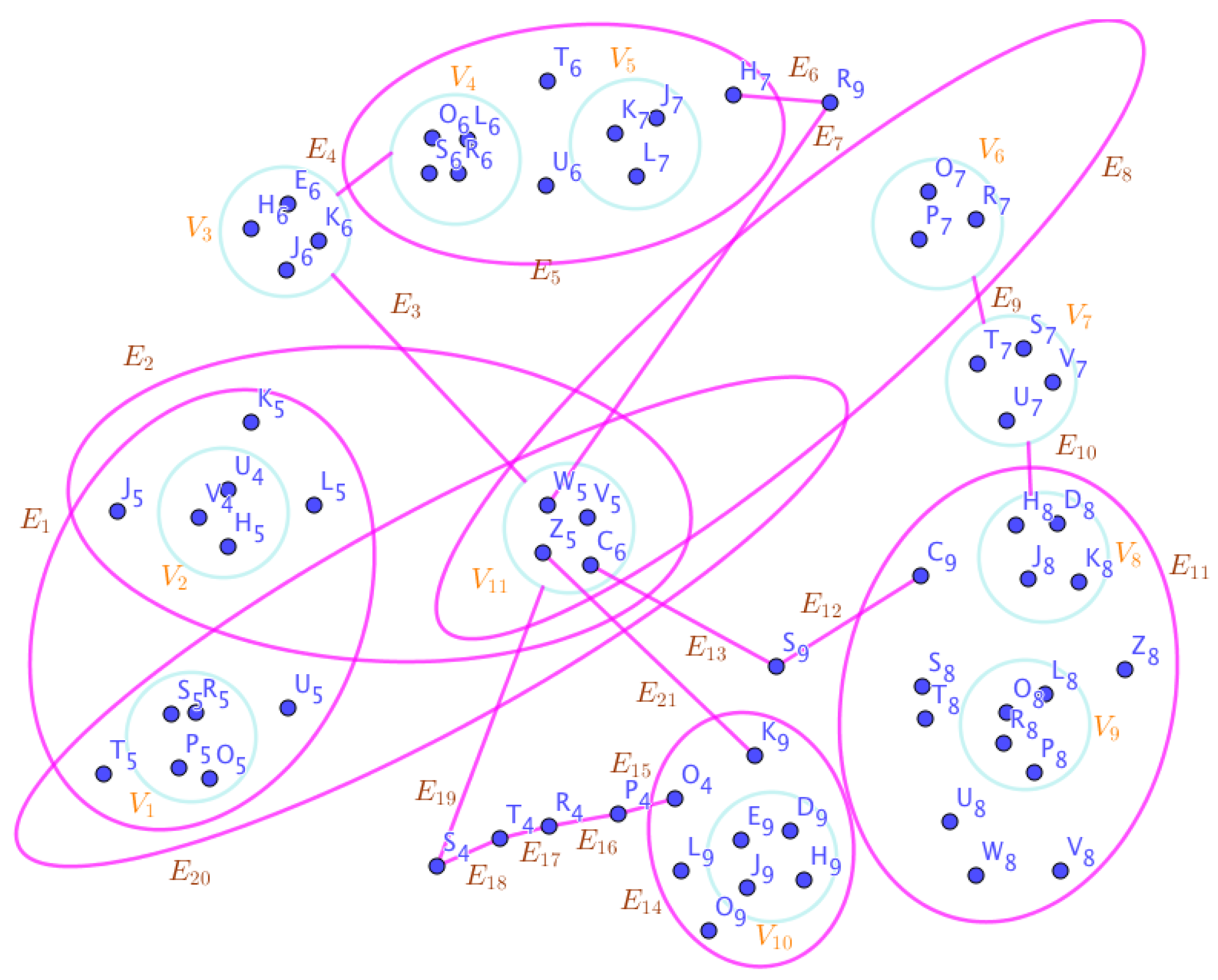
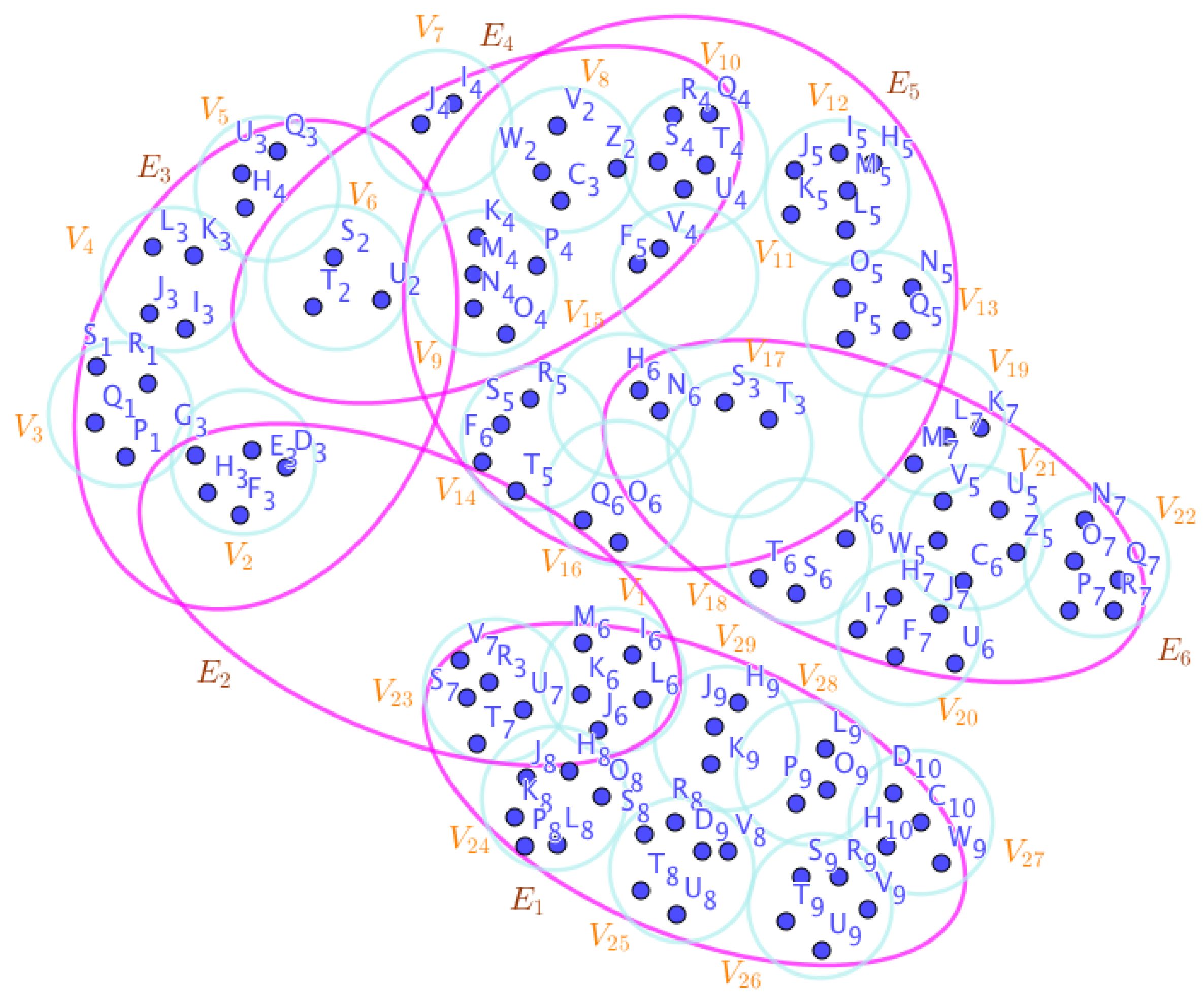
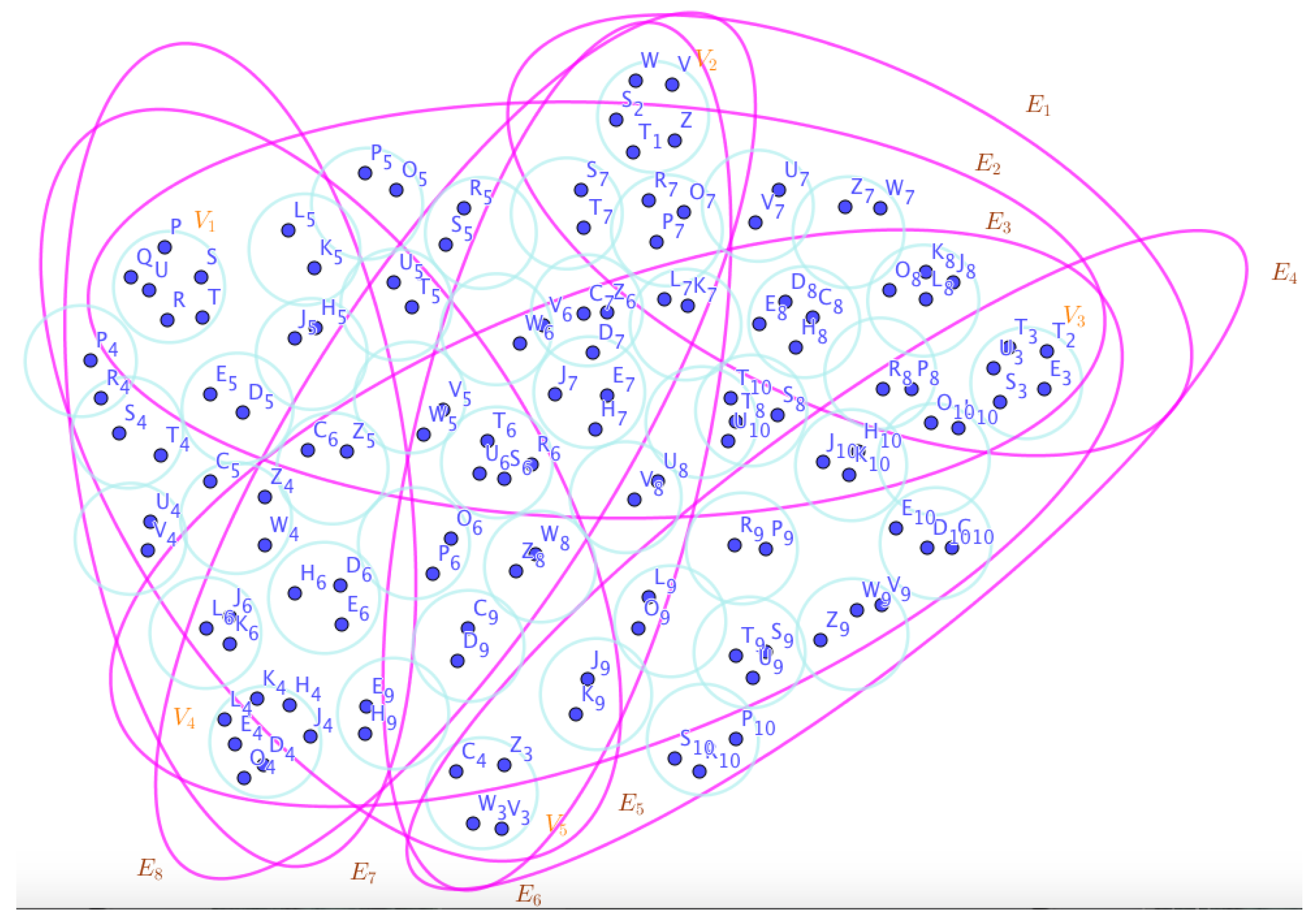
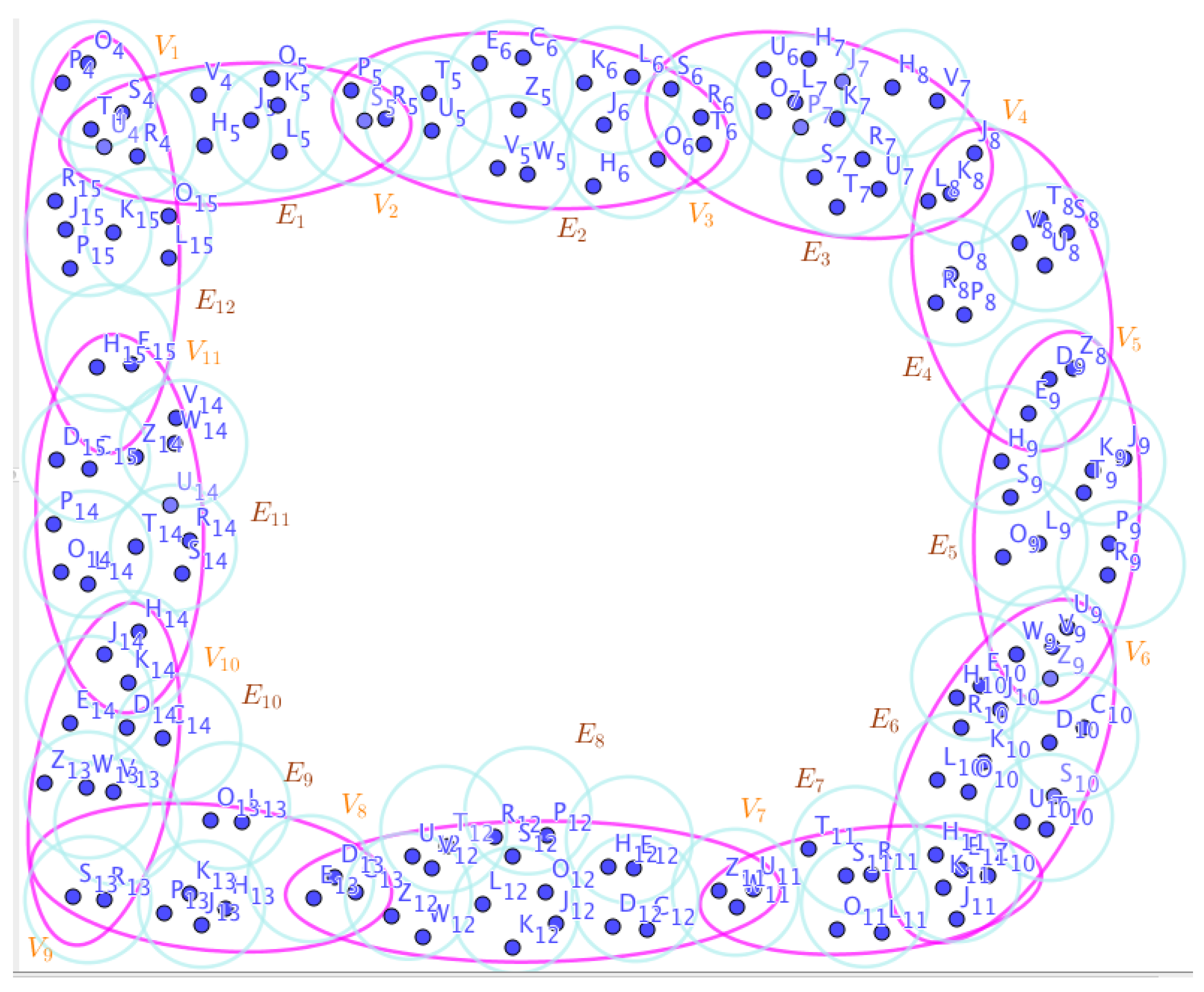
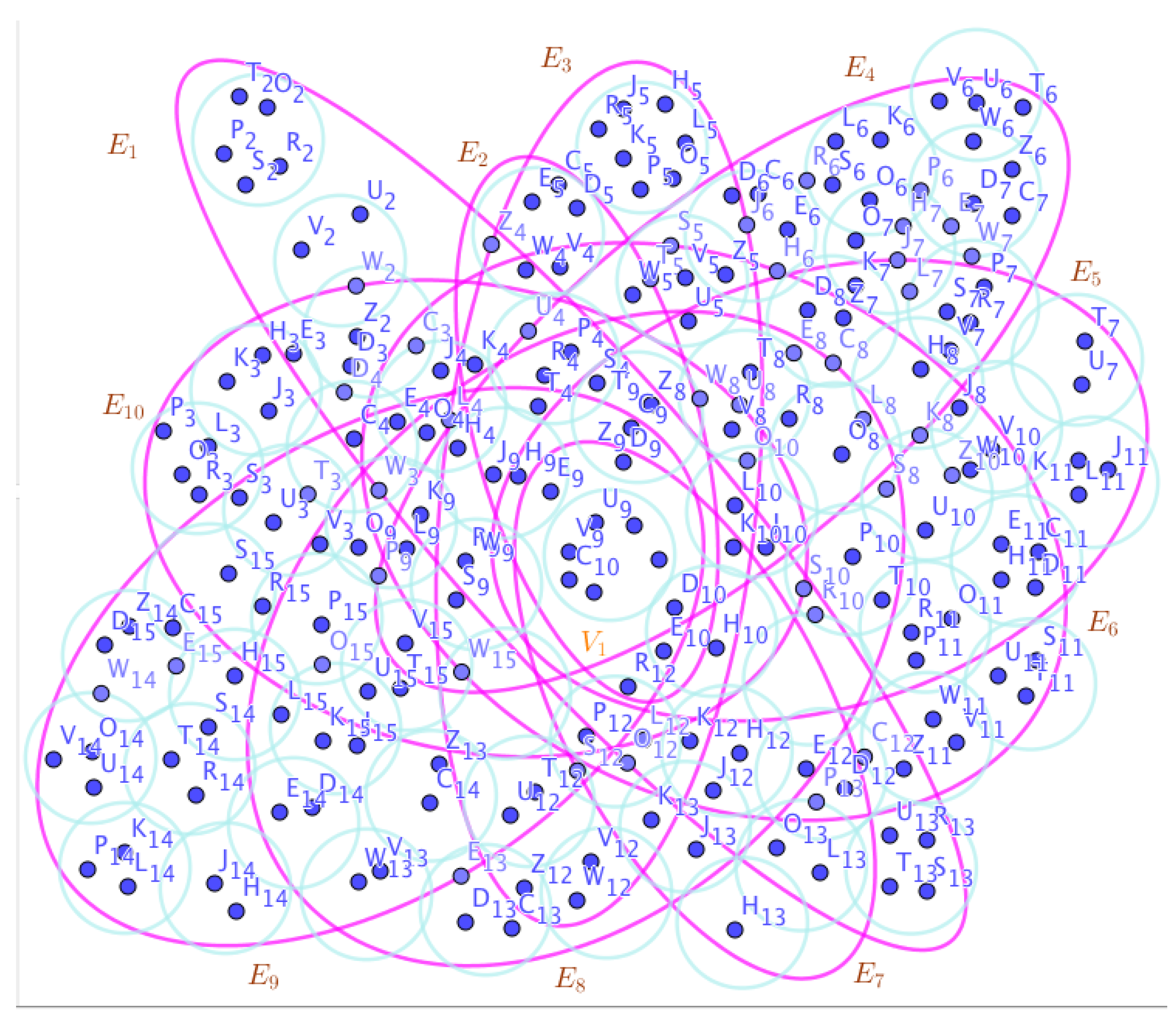
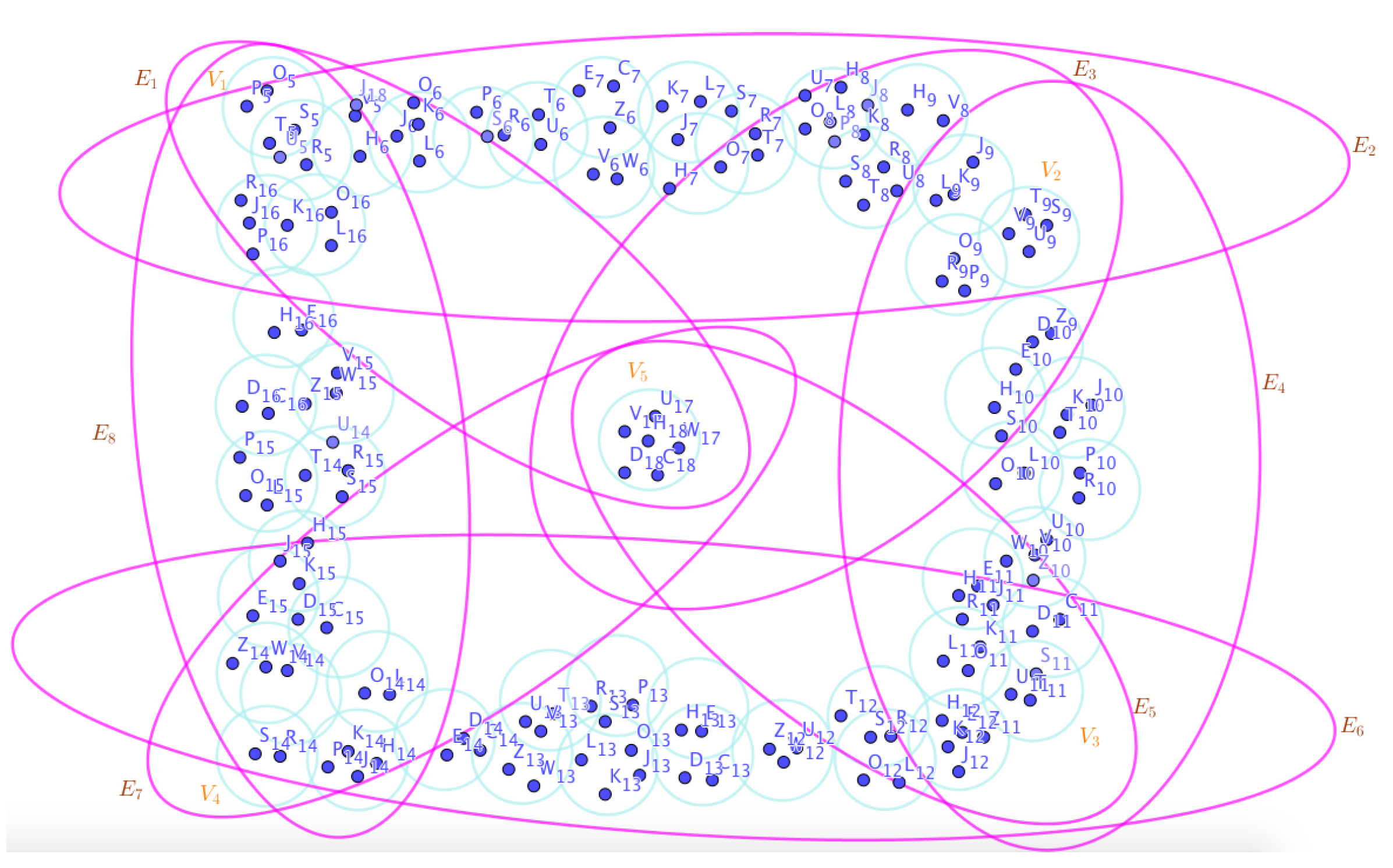
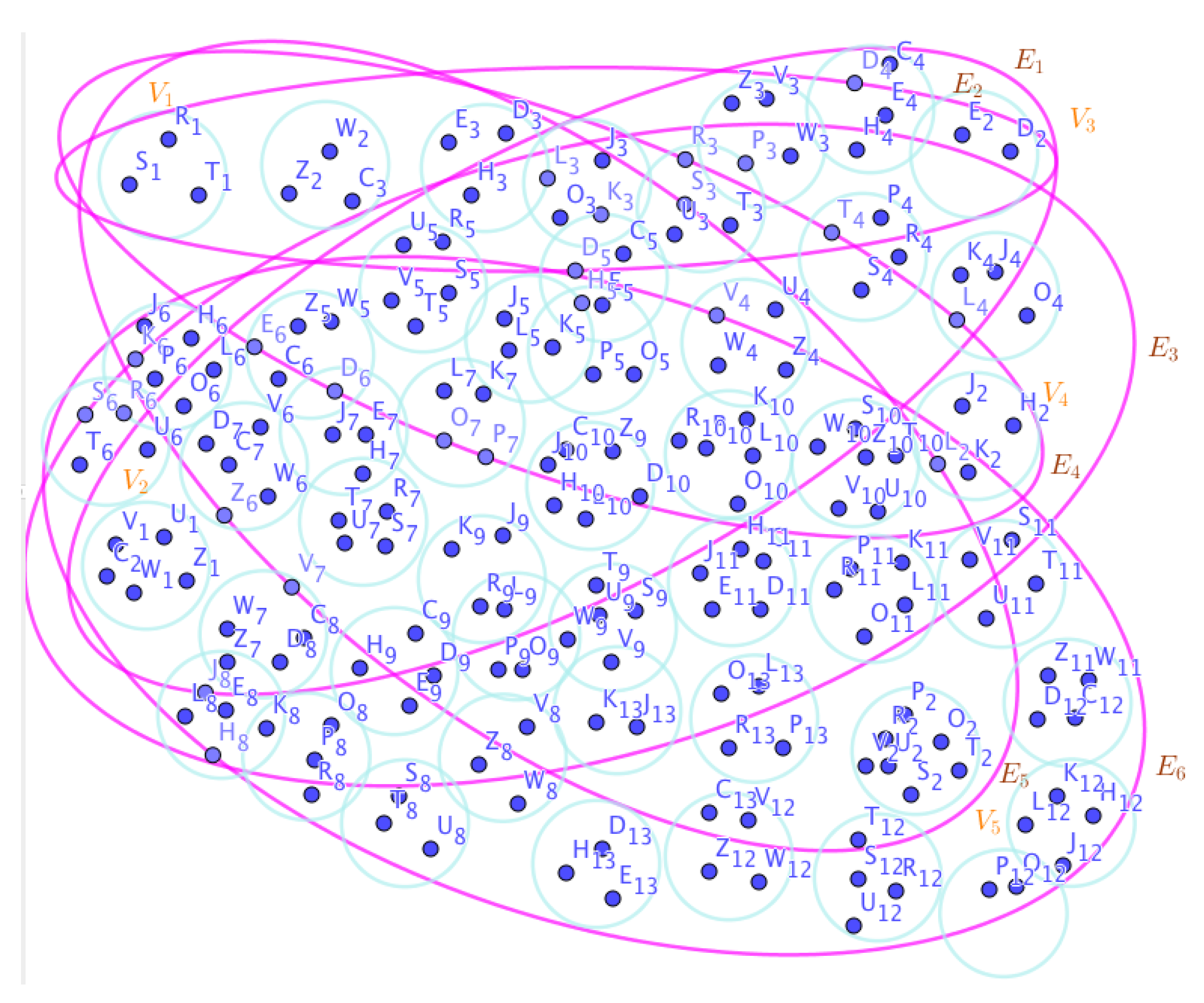
Example 23. 

Assume the neutrosophic SuperHyperGraphs in the Figures (1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), and (20).

• On the Figure (1), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. $E_1$ and $E_3$ are some empty neutrosophic SuperHyperEdges but $E_2$ is a loop neutrosophic SuperHyperEdge and $E_4$ is an neutrosophic SuperHyperEdge. Thus in the terms of neutrosophic SuperHyperNeighbor, there’s only one neutrosophic SuperHyperEdge, namely, $E_4.$ The neutrosophic SuperHyperVertex, $V_3$ is isolated means that there’s no neutrosophic SuperHyperEdge has it as an endpoint. Thus neutrosophic SuperHyperVertex, $V_3,$ is contained in every given neutrosophic 1-failed SuperHyperForcing. All the following neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices are the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing.

  $$\begin{array}{ccc}& & \{V_3,V_1\}\hfill \\ & & \{V_3,V_2\}\hfill \\ & & \{V_3,V_4\}\hfill \end{array}$$
  The neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ are the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ are the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing aren’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ don’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing aren’t up. To sum them up, the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ aren’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ are the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSets, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ aren’t up. The obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ are a neutrosophic SuperHyperSets, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ It’s interesting to mention that the only obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing amid those obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing, is only $\{V_3,V_2\}.$
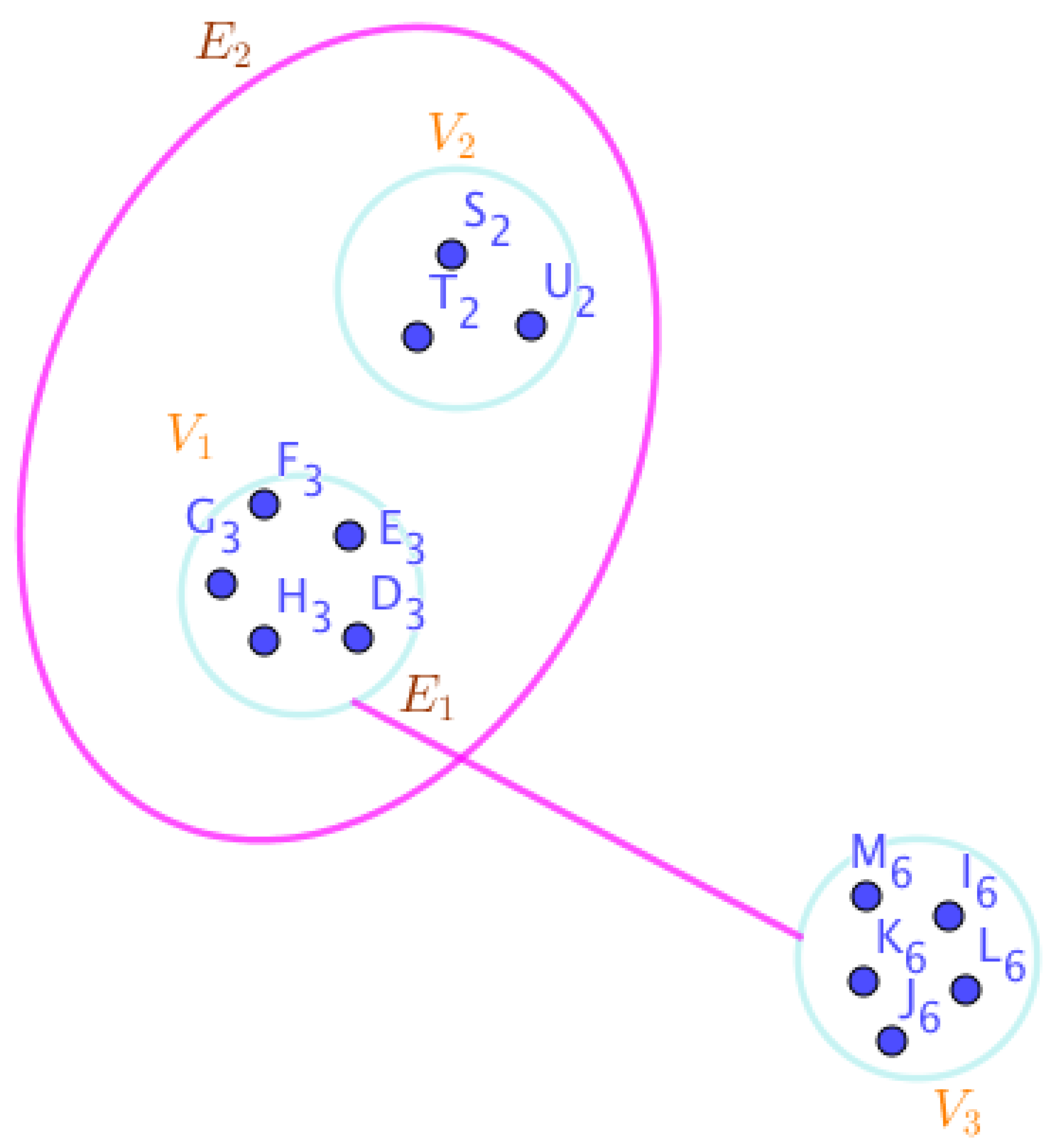
• On the Figure (2), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. $E_1,E_2$ and $E_3$ are some empty neutrosophic SuperHyperEdges but $E_4$ is an neutrosophic SuperHyperEdge. Thus in the terms of neutrosophic SuperHyperNeighbor, there’s only one neutrosophic SuperHyperEdge, namely, $E_4.$ The neutrosophic SuperHyperVertex, $V_3$ is isolated means that there’s no neutrosophic SuperHyperEdge has it as an endpoint. Thus neutrosophic SuperHyperVertex, $V_3,$ is contained in every given neutrosophic 1-failed SuperHyperForcing. All the following neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices are the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing.

  $$\begin{array}{ccc}& & \{V_3,V_1\}\hfill \\ & & \{V_3,V_2\}\hfill \\ & & \{V_3,V_4\}\hfill \end{array}$$
  The neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ are the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ are the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing aren’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ don’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing aren’t up. To sum them up, the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$aren’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ are the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSets, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ aren’t up. The obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ are a neutrosophic SuperHyperSets, $\{V_3,V_1\},\{V_3,V_2\},\{V_3,V_4\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ It’s interesting to mention that the only obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing amid those obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing, is only $\{V_3,V_2\}.$
• On the Figure (3), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. $E_1,E_2$ and $E_3$ are some empty neutrosophic SuperHyperEdges but $E_4$ is an neutrosophic SuperHyperEdge. Thus in the terms of neutrosophic SuperHyperNeighbor, there’s only one neutrosophic SuperHyperEdge, namely, $E_4.$ The neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\},$ are the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\},$ are the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing aren’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\},$ don’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing aren’t up. To sum them up, the neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\},$aren’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSets of the neutrosophic SuperHyperVertices, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\},$ are the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since they’ve the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSets, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\},$ aren’t up. The obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\},$ are the neutrosophic SuperHyperSets, $\left\{V_1\right\},\left\{V_2\right\},\left\{V_3\right\},$ don’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ It’s interesting to mention that the only obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing amid those obvious simple type-neutrosophic SuperHyperSets of the neutrosophic 1-failed SuperHyperForcing, is only $\left\{V_1\right\}.$
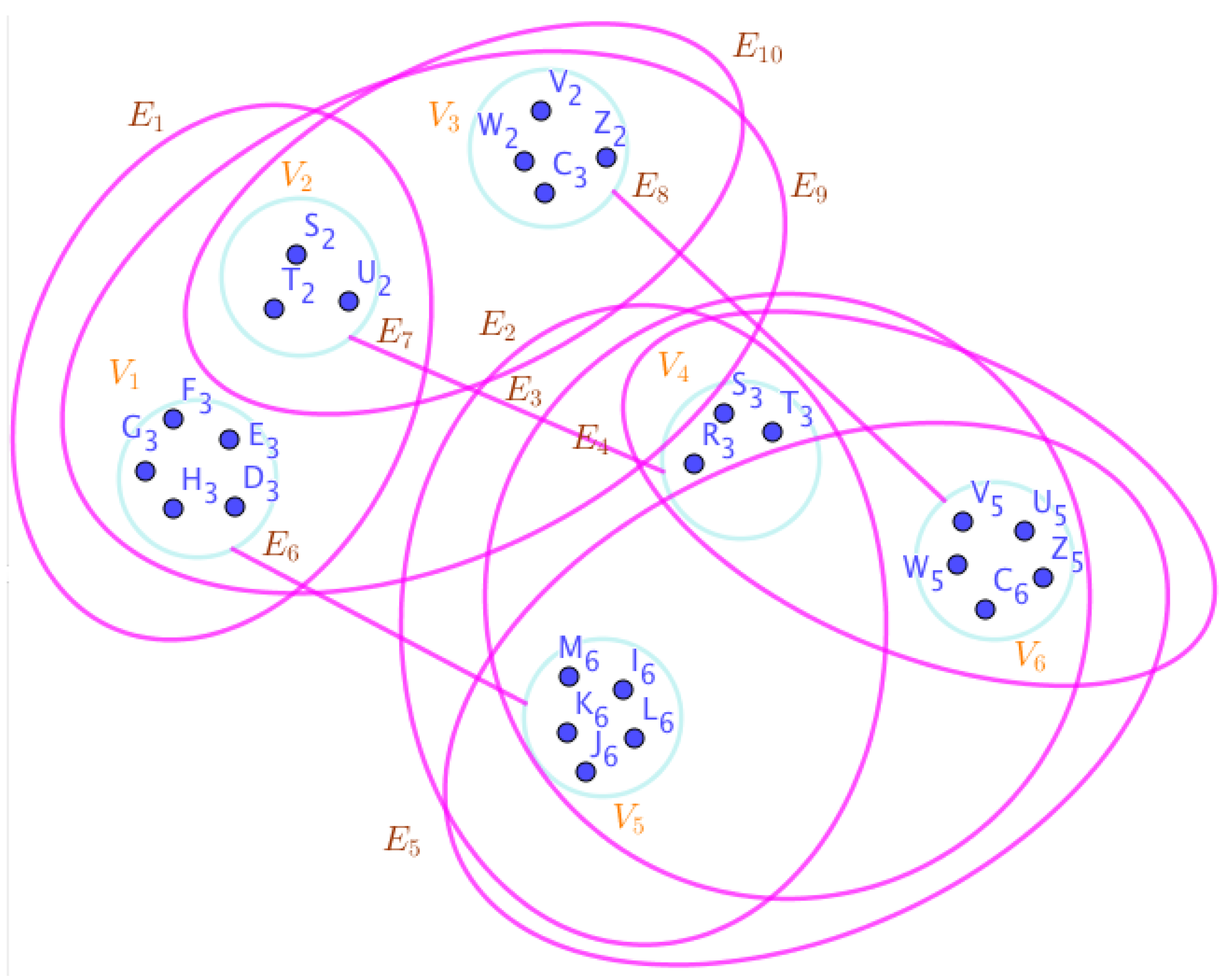
• On the Figure (4), the neutrosophic SuperHyperNotion, namely, an neutrosophic 1-failed SuperHyperForcing, is up. There’s no empty neutrosophic SuperHyperEdge but $E_3$ are a loop neutrosophic SuperHyperEdge on $\left\{F\right\},$ and there are some neutrosophic SuperHyperEdges, namely, $E_1$ on $\{H,V_1,V_3\},$ alongside $E_2$ on $\{O,H,V_4,V_3\}$ and $E_4,E_5$ on $\{N,V_1,V_2,V_3,F\}.$ The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_1,V_2,V_3,V_4,O,H\},$ is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_1,V_2,V_3,V_4,O,H\},$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_1,V_2,V_3,V_4,O,H\},$ doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_1,V_2,V_3,V_4,O,H\},$isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_1,V_2,V_3,V_4,O,H\},$ is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $\{V_1,V_2,V_3,V_4,O,H\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\{V_1,V_2,V_3,V_4,O,H\},$ isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $\{V_1,V_2,V_3,V_4,O,H\},$ is a neutrosophic SuperHyperSet, $\{V_1,V_2,V_3,V_4,O,H\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$
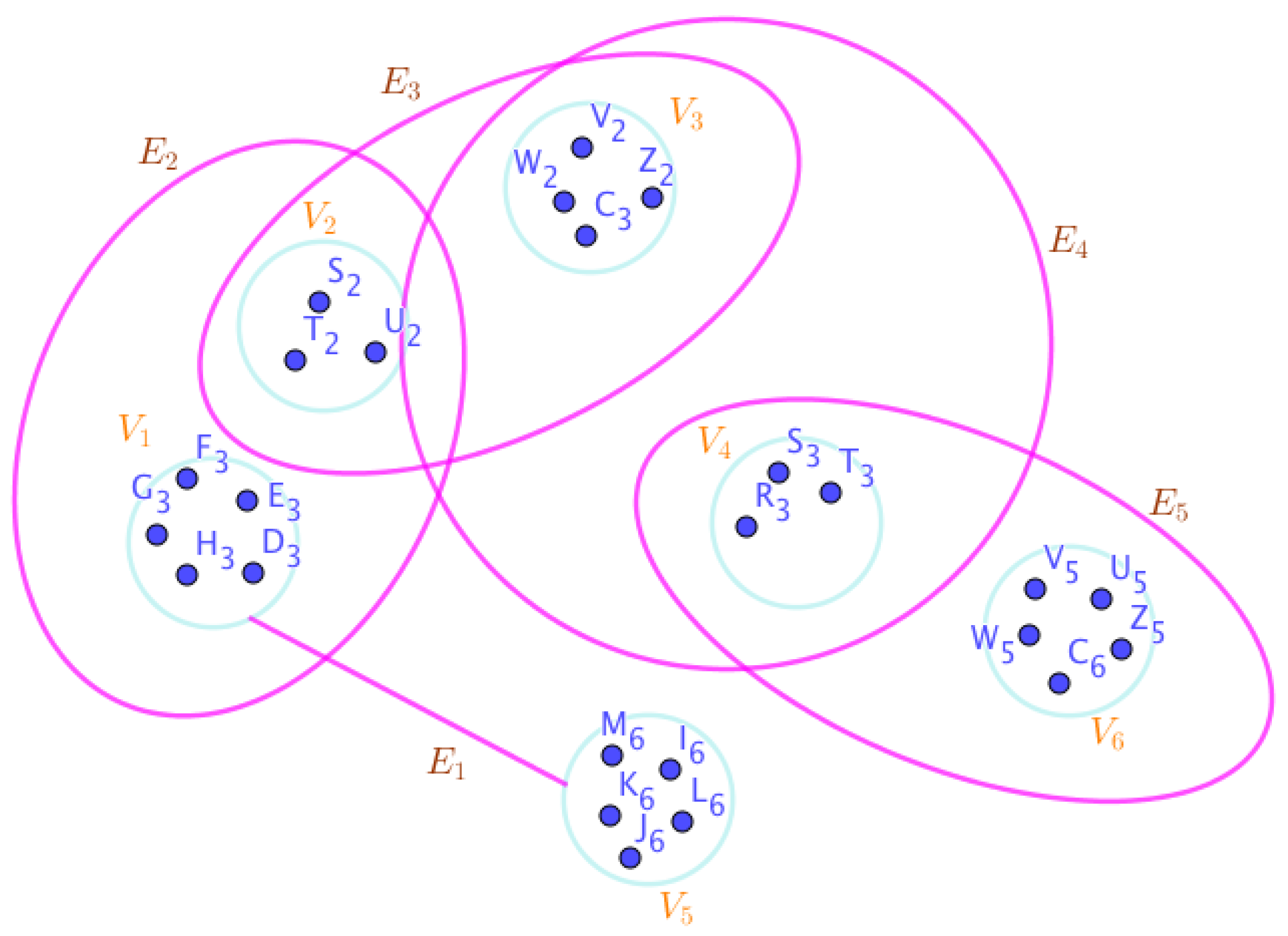
• On the Figure (5), the neutrosophic SuperHyperNotion, namely, SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\},$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\},$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\},$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\},$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\},$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\}.$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\},$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\},$$

  is a neutrosophic SuperHyperSet,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15}\},$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E)$ is mentioned as the SuperHyperModel $NSHG:(V,E)$ in the Figure (5).
• On the Figure (6), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\}.$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  is a neutrosophic SuperHyperSet,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E)$ with a illustrated SuperHyperModeling of the Figure (6).
• On the Figure (7), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\}.$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is a neutrosophic SuperHyperSet,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E)$ of depicted SuperHyperModel as the Figure (7).
• On the Figure (8), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\}.$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is a neutrosophic SuperHyperSet,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E)$ of dense SuperHyperModel as the Figure (8).
• On the Figure (9), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\}.$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  is a neutrosophic SuperHyperSet,

  $$\{V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},V_{19},V_{20},V_{22}\},$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E)$ with a messy SuperHyperModeling of the Figure (9).
• On the Figure (10), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\}.$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  is a neutrosophic SuperHyperSet,

  $$\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14}\},$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E)$ of highly-embedding-connected SuperHyperModel as the Figure (10).
• On the Figure (11), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$ is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$ doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$ is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’sthe maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $\{V_2,V_4,V_5,V_6\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\{V_2,V_4,V_5,V_6\},$ isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $\{V_2,V_4,V_5,V_6\},$ is a neutrosophic SuperHyperSet, $\{V_2,V_4,V_5,V_6\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$
• On the Figure (12), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\},$ is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\},$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\},$ doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\},$isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\},$ is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\},$ isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\},$ is a neutrosophic SuperHyperSet, $\{V_2,V_4,V_5,V_6,V_7,V_8,V_9,V_{10}\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E)$ in highly-multiple-connected-style SuperHyperModel On the Figure (12).
• On the Figure (13), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$ is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$ doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_2,V_4,V_5,V_6\},$ is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $\{V_2,V_4,V_5,V_6\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\{V_2,V_4,V_5,V_6\},$ isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $\{V_2,V_4,V_5,V_6\},$ is a neutrosophic SuperHyperSet, $\{V_2,V_4,V_5,V_6\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$
• On the Figure (14), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\left\{V_2\right\},$ is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\left\{V_2\right\},$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\left\{V_2\right\},$ doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\left\{V_2\right\},$isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\left\{V_2\right\},$ is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $\left\{V_2\right\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\left\{V_2\right\},$ isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $\left\{V_2\right\},$ is a neutrosophic SuperHyperSet, $\left\{V_2\right\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$
• On the Figure (15), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_1,V_4,V_5,V_6\},$ is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_1,V_4,V_5,V_6\},$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_1,V_4,V_5,V_6\},$ doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_1,V_4,V_5,V_6\},$isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_1,V_4,V_5,V_6\},$ is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $\{V_1,V_4,V_5,V_6\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\{V_1,V_4,V_5,V_6\},$ isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $\{V_1,V_4,V_5,V_6\},$ is a neutrosophic SuperHyperSet, $\{V_1,V_4,V_5,V_6\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ as Linearly-Connected SuperHyperModel On the Figure (15).
• On the Figure (16), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\},\hfill \end{array}$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\},\hfill \end{array}$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\},\hfill \end{array}$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\},\hfill \end{array}$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\},\hfill \end{array}$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\}.\hfill \end{array}$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\},\hfill \end{array}$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\},\hfill \end{array}$$

  is a neutrosophic SuperHyperSet,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22}\},\hfill \end{array}$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$
• On the Figure (17), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\}.\hfill \end{array}$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$

  is a neutrosophic SuperHyperSet,

  $$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E)$ as Lnearly-over-packed SuperHyperModel is featured On the Figure (17).
• On the Figure (18), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,R,M_6,L_6,F,P,J,M\},$ is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_2,R,M_6,L_6,F,P,J,M\},$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,R,M_6,L_6,F,P,J,M\},$ doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices, $\{V_2,R,M_6,L_6,F,P,J,M\},$isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices, $\{V_2,R,M_6,L_6,F,P,J,M\},$ is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $\{V_2,R,M_6,L_6,F,P,J,M\}.$ Thus the non-obvious neutrosophic 1-failed SuperHyperForcing, $\{V_2,R,M_6,L_6,F,P,J,M\},$ isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $\{V_2,R,M_6,L_6,F,P,J,M\},$ is a neutrosophic SuperHyperSet, $\{V_2,R,M_6,L_6,F,P,J,M\},$ doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$
• On the Figure (19), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\},\hfill \end{array}$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\},\hfill \end{array}$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\},\hfill \end{array}$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\},\hfill \end{array}$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\},\hfill \end{array}$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\}.\hfill \end{array}$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\},\hfill \end{array}$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\},\hfill \end{array}$$

  is a neutrosophic SuperHyperSet,

  $$\begin{array}{ccc}& & \{T_3,S_3,U_3,V_4,V_5,V_6,V_7,V_8,V_9,V_{10},R_6,S_6,Z_5,W_5,T_6\hfill \\ & & H_6,O_6,E_6,C_6,V_2,R,M_6,L_6,F,P,J,M\},\hfill \end{array}$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$
• On the Figure (20), the neutrosophic SuperHyperNotion, namely, neutrosophic 1-failed SuperHyperForcing, is up. There’s neither empty neutrosophic SuperHyperEdge nor loop neutrosophic SuperHyperEdge. The neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$

  is the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$

  is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious neutrosophic 1-failed SuperHyperForcing isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing is a neutrosophic SuperHyperSet excludes only two neutrosophic SuperHyperVertices are titled to neutrosophic SuperHyperNeighbors in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ But the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$

  doesn’t have more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet. Thus the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing isn’t up. To sum them up, the neutrosophic SuperHyperSet of neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$
  isn’t the non-obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$

  is the neutrosophic SuperHyperSet Ss of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex and they are neutrosophic 1-failed SuperHyperForcing. Since it’s the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. There aren’t only more than two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$
  Thus the non-obvious neutrosophic 1-failed SuperHyperForcing,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$

  isn’t up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$

  is a neutrosophic SuperHyperSet,

  $$\begin{array}{ccc}& & \{V_2,V_3,V_4,T_6,U_6,H_7,V_5,R_9,\hfill \\ & & V_6,V_7,V_8,V_9,v_8,W_8,U_8,S_8,T_8,C_9,Z_8,S_9\hfill \\ & & K_9,O_9,L_9,O_4,V_{10},P_4,R_4,T_4,S_4\},\hfill \end{array}$$

  doesn’t exclude only more than two neutrosophic SuperHyperVertices in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$

Figure 1. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 1. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 2. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 2. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 3. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 3. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 4. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 4. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 5. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 5. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 6. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 6. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 7. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 7. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 8. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 8. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 9. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 9. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 10. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 10. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 11. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 11. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 12. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 12. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 13. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 13. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 14. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 14. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 15. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 15. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 16. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 16. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 17. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 17. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 18. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 18. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 19. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 19. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 20. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Figure 20. The neutrosophic SuperHyperGraphs Associated to the Notions of neutrosophic 1-failed SuperHyperForcing in the Examples () and (23).

Proposition 24. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ Then in the worst case, literally, $V\setminus \{x,z\}$ is an neutrosophic 1-failed SuperHyperForcing. In other words, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, of neutrosophic 1-failed SuperHyperForcing is the neutrosophic cardinality of $V\setminus \{x,z\}.$

Proof. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. □

Proposition 25. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ Then the extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the extreme neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality.

Proof. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ Consider there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the extreme neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. □

Proposition 26. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ If a neutrosophic SuperHyperEdge has z neutrosophic SuperHyperVertices, then $z-2$ number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any neutrosophic 1-failed SuperHyperForcing.

Proof. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ Let a neutrosophic SuperHyperEdge has z neutrosophic SuperHyperVertices. Consider $z-3$ number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the extreme neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus all the following neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices are the simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing. It’s the contradiction to the neutrosophic SuperHyperSet either $S=V\setminus \{x,y,z\}$ or $S=V\setminus \left\{x\right\}$ is an neutrosophic 1-failed SuperHyperForcing. Thus any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices contains the number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge with z neutrosophic SuperHyperVertices less than $z-2$ isn’t an neutrosophic 1-failed SuperHyperForcing. Thus if a neutrosophic SuperHyperEdge has z neutrosophic SuperHyperVertices, then $z-2$ number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any neutrosophic 1-failed SuperHyperForcing. □

Proposition 27. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ There’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of an neutrosophic 1-failed SuperHyperForcing. In other words, there’s an unique neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices.

Proof. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the extreme neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any neutrosophic 1-failed SuperHyperForcing. Thus, in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of neutrosophic 1-failed SuperHyperForcing. In other words, there’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices which are neutrosophic SuperHyperNeighbors. □

Proposition 28. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ The all exterior neutrosophic SuperHyperVertices belong to any neutrosophic 1-failed SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors.

Proof. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the extreme neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any neutrosophic 1-failed SuperHyperForcing. Thus, in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of neutrosophic 1-failed SuperHyperForcing. In other words, here’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices. In a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ the all exterior neutrosophic SuperHyperVertices belong to any neutrosophic 1-failed SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors. □

Proposition 29. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ The any neutrosophic 1-failed SuperHyperForcing only contains all interior neutrosophic SuperHyperVertices and all exterior neutrosophic SuperHyperVertices where there’s any of them has two neutrosophic SuperHyperNeighbors out.

Proof. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an neutrosophic 1-failed SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the neutrosophic 1-failed SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the extreme number of neutrosophic 1-failed SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the extreme neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an neutrosophic 1-failed SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any neutrosophic 1-failed SuperHyperForcing. Thus, in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of neutrosophic 1-failed SuperHyperForcing. In other words, here’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices. In a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ the all exterior neutrosophic SuperHyperVertices belong to any neutrosophic 1-failed SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors. Thus in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ any neutrosophic 1-failed SuperHyperForcing only contains all interior neutrosophic SuperHyperVertices and all exterior neutrosophic SuperHyperVertices where there’s any of them has two neutrosophic SuperHyperNeighbors out. □

Remark 30.

The words “neutrosophic 1-failed SuperHyperForcing” and “neutrosophic SuperHyperDominating” refer to the maximum type-style and the minimum type-style. In other words, they refer to both the maximum[minimum] number and the neutrosophic SuperHyperSet with the maximum[minimum] neutrosophic cardinality.

Proposition 31. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ An neutrosophic 1-failed SuperHyperForcing contains the neutrosophic SuperHyperDominating.

Proof. 

Assume a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E).$ By applying the Proposition (29), the results are up. Thus in a connected neutrosophic SuperHyperNotion SuperHyperGraph $NSHG:(V,E),$ an neutrosophic 1-failed SuperHyperForcing contains the neutrosophic SuperHyperDominating. □

3. Results on Neutrosophic SuperHyperClasses

Proposition 32. 

Assume a connected neutrosophic SuperHyperPath $NSHP:(V,E).$ Then an 1-failed neutrosophic SuperHyperForcing-style with the maximum neutrosophic cardinality is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices.

Proposition 33. 

Assume a connected neutrosophic SuperHyperPath $NSHP:(V,E).$ Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices with only two exceptions in the form of interior neutrosophic SuperHyperVertices from the same neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of all the neutrosophic SuperHyperVertices minus two. Thus,

$$\begin{array}{ccc}& & Neutrosophic1-failedSuperHyperForcing=\{\mathit{The}\mathit{number}-\mathit{of}-\mathit{all}\hfill \\ & & -\mathit{the}-\mathit{SuperHyperVertices}\hfill \\ & & -\mathit{minus}-\mathit{on}-\mathit{two}-\mathit{numbers}-\mathit{of}-\mathit{interior}-\mathit{SuperHyperNeighbors}\hfill \\ & & \mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}|min|\mathit{the}\hfill \\ & & \mathit{SuperHyperSets}\mathit{of}\mathit{the}\mathit{SuperHyperVertices}\mathit{with}\mathit{only}\hfill \\ & & \mathit{two}\mathit{exceptions}\mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\mathit{SuperHyperVertices}\mathit{from}\mathit{any}\mathit{same}\hfill \\ & & {\mathit{SuperHyperEdge}.|}_{\mathit{neutrosophic}\mathit{cardinality}\mathit{amid}\mathit{those}\mathit{SuperHyperSets}.}\}\hfill \end{array}$$

Where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively.

Proof. 

Assume a connected neutrosophic SuperHyperPath $NSHP:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some neutrosophic numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all neutrosophic number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any 1-failed neutrosophic SuperHyperForcing. Thus, in a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of 1-failed neutrosophic SuperHyperForcing. In other words, here’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices. In a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ the all exterior neutrosophic SuperHyperVertices belong to any 1-failed neutrosophic SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors. Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices with only two exceptions in the form of interior neutrosophic SuperHyperVertices from the same neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of all the neutrosophic SuperHyperVertices minus two. Thus,

$$\begin{array}{ccc}& & Neutrosophic1-failedSuperHyperForcing=\{\mathrm{The}\mathrm{number}-\mathrm{of}-\mathrm{all}\hfill \\ & & -\mathrm{the}-\mathrm{SuperHyperVertices}\hfill \\ & & -\mathrm{minus}-\mathrm{on}-\mathrm{two}-\mathrm{numbers}-\mathrm{of}-\mathrm{interior}-\mathrm{SuperHyperNeighbors}\hfill \\ & & \mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\hfill \\ & & \mathrm{SuperHyperVertices}|min|\mathrm{the}\hfill \\ & & \mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\mathrm{SuperHyperVertices}\mathrm{with}\mathrm{only}\hfill \\ & & \mathrm{two}\mathrm{exceptions}\mathrm{in}\mathrm{the}\mathrm{form}\mathrm{of}\mathrm{interior}\mathrm{SuperHyperVertices}\mathrm{from}\mathrm{any}\mathrm{same}\hfill \\ & & {\mathrm{SuperHyperEdge}.|}_{\mathrm{neutrosophic}\mathrm{cardinality}\mathrm{amid}\mathrm{those}\mathrm{SuperHyperSets}.}\}\hfill \end{array}$$

where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively. □

Example 34. 

In the Figure (21), the connected neutrosophic SuperHyperPath $NSHP:(V,E),$ is highlighted and featured.

Figure 21. A neutrosophic SuperHyperPath Associated to the Notions of 1-failed neutrosophic SuperHyperForcing in the Example (34).

Figure 21. A neutrosophic SuperHyperPath Associated to the Notions of 1-failed neutrosophic SuperHyperForcing in the Example (34).

By using the Figure (21) and the Table (4), the neutrosophic SuperHyperPath is obtained.

The neutrosophic SuperHyperSet,

$$\begin{array}{ccc}& & \{V_1,V_2,V_5,V_6,V_7,V_8,V_9,V_{10},V_{11},V_{12},V_{13},V_{14},V_{15},V_{16},V_{17},V_{18},\hfill \\ & & V_{19},V_{20},V_{21},V_{22},V_{23},V_{24},V_{25},V_{26},V_{27},V_{28},V_{29}\},\hfill \end{array}$$

of the neutrosophic SuperHyperVertices of the connected neutrosophic SuperHyperPath $NSHP:(V,E),$ in the neutrosophic SuperHyperModel (21), is the 1-failed neutrosophic SuperHyperForcing.

Table 4. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperPath Mentioned in the Example (34)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 4. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperPath Mentioned in the Example (34)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Proposition 35. 

Assume a connected neutrosophic SuperHyperCycle $NSHC:(V,E).$ Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices with only two exceptions in the form of interior neutrosophic SuperHyperVertices from the same neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of all the neutrosophic SuperHyperVertices minus on the 2 neutrosophic numbers excerpt the same exterior neutrosophic SuperHyperPart. Thus,

$$\begin{array}{ccc}& & Neutrosophic1-failedSuperHyperForcing=\{\mathit{The}\mathit{number}-\mathit{of}-\mathit{all}\hfill \\ & & -\mathit{the}-\mathit{SuperHyperVertices}\hfill \\ & & -\mathit{minus}-\mathit{on}-2-\mathit{numbers}-\mathit{of}-\mathit{same}-\mathit{exterior}-\mathit{SuperHyperPart}\hfill \\ & & \mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}|min|\mathit{the}\mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}\mathit{with}\mathit{only}\hfill \\ & & \mathit{two}\mathit{exceptions}\mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\mathit{SuperHyperVertices}\hfill \\ & & \mathit{from}\mathit{same}\hfill \\ & & \mathit{neutrosophic}\hfill \\ & & {\mathit{SuperHyperEdge}.|}_{\mathit{neutrosophic}\mathit{cardinality}\mathit{amid}\mathit{those}\mathit{SuperHyperSets}.}\}\hfill \end{array}$$

Where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively.

Proof. 

Assume a connected neutrosophic SuperHyperCycle $NSHC:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some neutrosophic numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all neutrosophic number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any 1-failed neutrosophic SuperHyperForcing. Thus, in a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of 1-failed neutrosophic SuperHyperForcing. In other words, here’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices. In a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ the all exterior neutrosophic SuperHyperVertices belong to any 1-failed neutrosophic SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors. Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices with only two exceptions in the form of interior neutrosophic SuperHyperVertices from the same neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of all the neutrosophic SuperHyperVertices minus on the 2 neutrosophic numbers excerpt the same exterior neutrosophic SuperHyperPart. Thus,

$$\begin{array}{ccc}& & Neutrosophic1-failedSuperHyperForcing=\{\mathrm{The}\mathrm{number}-\mathrm{of}-\mathrm{all}\hfill \\ & & -\mathrm{the}-\mathrm{SuperHyperVertices}\hfill \\ & & -\mathrm{minus}-\mathrm{on}-2-\mathrm{numbers}-\mathrm{of}-\mathrm{same}-\mathrm{exterior}-\mathrm{SuperHyperPart}\hfill \\ & & \mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\hfill \\ & & \mathrm{SuperHyperVertices}|min|\mathrm{the}\mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\hfill \\ & & \mathrm{SuperHyperVertices}\mathrm{with}\mathrm{only}\hfill \\ & & \mathrm{two}\mathrm{exceptions}\mathrm{in}\mathrm{the}\mathrm{form}\mathrm{of}\mathrm{interior}\mathrm{SuperHyperVertices}\hfill \\ & & \mathrm{from}\mathrm{same}\hfill \\ & & \mathrm{neutrosophic}\hfill \\ & & {\mathrm{SuperHyperEdge}.|}_{\mathrm{neutrosophic}\mathrm{cardinality}\mathrm{amid}\mathrm{those}\mathrm{SuperHyperSets}.}\}\hfill \end{array}$$

Where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively. □

Example 36. 

In the Figure (22), the connected neutrosophic SuperHyperCycle $NSHC:(V,E),$ is highlighted and featured.

By using the Figure (22) and the Table ((5)), the neutrosophic SuperHyperCycle is obtained.

The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected neutrosophic SuperHyperCycle $NSHC:(V,E),$ in the neutrosophic SuperHyperModel (22), is the 1-failed neutrosophic SuperHyperForcing.

Table 5. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperCycle Mentioned in the Example (36)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 5. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperCycle Mentioned in the Example (36)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Proposition 37. 

Assume a connected neutrosophic SuperHyperStar $NSHS:(V,E).$ Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices, excluding the neutrosophic SuperHyperCenter, with only one exception in the form of interior neutrosophic SuperHyperVertices from any given neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of the neutrosophic cardinality of the second neutrosophic SuperHyperPart minus one. Thus,

$$\begin{array}{ccc}& & \mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{s}\mathit{o}\mathit{p}\mathit{h}\mathit{i}\mathit{c}1-\mathit{f}\mathit{a}\mathit{i}\mathit{l}\mathit{e}\mathit{d}\mathit{S}\mathit{u}\mathit{p}\mathit{e}\mathit{r}\mathit{H}\mathit{y}\mathit{p}\mathit{e}\mathit{r}\mathit{F}\mathit{o}\mathit{r}\mathit{c}\mathit{i}\mathit{n}\mathit{g}=\{\mathit{The}\mathit{number}-\mathit{of}-\mathit{all}\hfill \\ & & -\mathit{the}-\mathit{SuperHyperVertices}\hfill \\ & & -\mathit{of}-\mathit{the}-\mathit{cardinality}-\mathit{of}-\mathit{sec}\mathit{ond}-\mathit{SuperHyperPart}-\mathit{minus}-\mathit{one}\hfill \\ & & \mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}|min|\mathit{the}\mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}\mathit{with}\mathit{only}\hfill \\ & & \mathit{two}\mathit{exceptions}\mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\mathit{SuperHyperVertices}\mathit{from}\mathit{any}\hfill \\ & & {\mathit{given}\mathit{SuperHyperEdge}.|}_{\mathit{neutrosophic}\mathit{cardinality}\mathit{amid}\mathit{those}\mathit{SuperHyperSets}.}\}\hfill \end{array}$$

Where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively.

Proof. 

Assume a connected neutrosophic SuperHyperStar $NSHS:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some neutrosophic numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all neutrosophic number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any 1-failed neutrosophic SuperHyperForcing. Thus, in a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of 1-failed neutrosophic SuperHyperForcing. In other words, here’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices. In a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ the all exterior neutrosophic SuperHyperVertices belong to any 1-failed neutrosophic SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors. Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices, excluding the neutrosophic SuperHyperCenter, with only one exception in the form of interior neutrosophic SuperHyperVertices from any given neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of the neutrosophic cardinality of the second neutrosophic SuperHyperPart minus one. Thus,

$$\begin{array}{ccc}& & Neutrosophic1-failedSuperHyperForcing=\{\mathrm{The}\mathrm{number}-\mathrm{of}-\mathrm{all}\hfill \\ & & -\mathrm{the}-\mathrm{SuperHyperVertices}\hfill \\ & & -\mathrm{of}-\mathrm{the}-\mathrm{cardinality}-\mathrm{of}-\sec \mathrm{ond}-\mathrm{SuperHyperPart}-\mathrm{minus}-\mathrm{one}\hfill \\ & & \mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\hfill \\ & & \mathrm{SuperHyperVertices}|min|\mathrm{the}\mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\hfill \\ & & \mathrm{SuperHyperVertices}\mathrm{with}\mathrm{only}\hfill \\ & & \mathrm{two}\mathrm{exceptions}\mathrm{in}\mathrm{the}\mathrm{form}\mathrm{of}\mathrm{interior}\mathrm{SuperHyperVertices}\mathrm{from}\mathrm{any}\hfill \\ & & {\mathrm{given}\mathrm{SuperHyperEdge}.|}_{\mathrm{neutrosophic}\mathrm{cardinality}\mathrm{amid}\mathrm{those}\mathrm{SuperHyperSets}.}\}\hfill \end{array}$$

Where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively. □

Example 38. 

In the Figure (23), the connected neutrosophic SuperHyperStar $NSHS:(V,E),$ is highlighted and featured.

By using the Figure (23) and the Table (6), the neutrosophic SuperHyperStar is obtained.

The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected neutrosophic SuperHyperStar $NSHS:(V,E),$ in the neutrosophic SuperHyperModel (23), is the 1-failed neutrosophic SuperHyperForcing.

Table 6. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperStar Mentioned in the Example (38)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 6. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperStar Mentioned in the Example (38)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Proposition 39. 

Assume a connected neutrosophic SuperHyperBipartite $NSHB:(V,E).$ Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices with only two exceptions in the form of interior neutrosophic SuperHyperVertices from same neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of the neutrosophic cardinality of the first neutrosophic SuperHyperPart minus one plus the second neutrosophic SuperHyperPart minus one. Thus,

$$\begin{array}{ccc}& & \mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{s}\mathit{o}\mathit{p}\mathit{h}\mathit{i}\mathit{c}1-\mathit{f}\mathit{a}\mathit{i}\mathit{l}\mathit{e}\mathit{d}\mathit{S}\mathit{u}\mathit{p}\mathit{e}\mathit{r}\mathit{H}\mathit{y}\mathit{p}\mathit{e}\mathit{r}\mathit{F}\mathit{o}\mathit{r}\mathit{c}\mathit{i}\mathit{n}\mathit{g}=\{\mathit{The}\mathit{number}-\mathit{of}-\mathit{all}\hfill \\ & & -\mathit{the}-\mathit{SuperHyperVertices}\hfill \\ & & -\mathit{minus}-\mathit{on}-\mathit{the}-\mathit{cardinality}-\mathit{of}-\mathit{first}-\mathit{SuperHyperPart}-\mathit{minus}-1\hfill \\ & & -\mathit{plus}-\mathit{sec}\mathit{ond}-\mathit{SuperHyperPart}-\mathit{minus}-1\hfill \\ & & \mathit{SuperHyperSets}\mathit{of}\mathit{the}\mathit{SuperHyperVertices}|min|\hfill \\ & & \mathit{the}\mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}\mathit{with}\mathit{only}\mathit{two}\mathit{exceptions}\mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\hfill \\ & & \mathit{SuperHyperVertices}\mathit{from}\mathit{same}\mathit{SuperHyperEdge}.\hfill \\ & & {|}_{\mathit{neutrosophic}\mathit{cardinality}\mathit{amid}\mathit{those}\mathit{SuperHyperSets}.}\}\hfill \end{array}$$

Where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively.

Proof. 

Assume a connected neutrosophic SuperHyperBipartite $NSHB:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some neutrosophic numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all neutrosophic number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any 1-failed neutrosophic SuperHyperForcing. Thus, in a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of 1-failed neutrosophic SuperHyperForcing. In other words, here’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices. In a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ the all exterior neutrosophic SuperHyperVertices belong to any 1-failed neutrosophic SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors. Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices with only two exceptions in the form of interior neutrosophic SuperHyperVertices from same neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of the neutrosophic cardinality of the first neutrosophic SuperHyperPart minus one plus the second neutrosophic SuperHyperPart minus one. Thus,

$$\begin{array}{ccc}& & Neutrosophic1-failedSuperHyperForcing=\{\mathrm{The}\mathrm{number}-\mathrm{of}-\mathrm{all}\hfill \\ & & -\mathrm{the}-\mathrm{SuperHyperVertices}\hfill \\ & & -\mathrm{minus}-\mathrm{on}-\mathrm{the}-\mathrm{cardinality}-\mathrm{of}-\mathrm{first}-\mathrm{SuperHyperPart}-\mathrm{minus}-1\hfill \\ & & -\mathrm{plus}-\sec \mathrm{ond}-\mathrm{SuperHyperPart}-\mathrm{minus}-1\hfill \\ & & \mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\mathrm{SuperHyperVertices}|min|\hfill \\ & & \mathrm{the}\mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\hfill \\ & & \mathrm{SuperHyperVertices}\mathrm{with}\mathrm{only}\mathrm{two}\mathrm{exceptions}\mathrm{in}\mathrm{the}\mathrm{form}\mathrm{of}\mathrm{interior}\hfill \\ & & \mathrm{SuperHyperVertices}\mathrm{from}\mathrm{same}\mathrm{SuperHyperEdge}.\hfill \\ & & {|}_{\mathrm{neutrosophic}\mathrm{cardinality}\mathrm{amid}\mathrm{those}\mathrm{SuperHyperSets}.}\}\hfill \end{array}$$

Where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively. □

Example 40. 

In the Figure (24), the connected neutrosophic SuperHyperBipartite $NSHB:(V,E),$ is highlighted and featured.

Figure 24. A neutrosophic SuperHyperBipartite Associated to the Notions of 1-failed neutrosophic SuperHyperForcing in the Example (40).

Figure 24. A neutrosophic SuperHyperBipartite Associated to the Notions of 1-failed neutrosophic SuperHyperForcing in the Example (40).

By using the Figure (24) and the Table (7), the neutrosophic SuperHyperBipartite $NSHB:(V,E),$ is obtained.

The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected neutrosophic SuperHyperBipartite $NSHB:(V,E),$ in the neutrosophic SuperHyperModel (24), is the 1-failed neutrosophic SuperHyperForcing.

Table 7. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperBipartite Mentioned in the Example (40)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 7. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperBipartite Mentioned in the Example (40)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Proposition 41. 

Assume a connected neutrosophic SuperHyperMultipartite $NSHM:(V,E).$ Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices with only one exception in the form of interior neutrosophic SuperHyperVertices from a neutrosophic SuperHyperPart and only one exception in the form of interior neutrosophic SuperHyperVertices from another neutrosophic SuperHyperPart. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of all the summation on the neutrosophic cardinality of the all neutrosophic SuperHyperParts minus two excerpt distinct neutrosophic SuperHyperParts. Thus,

$$\begin{array}{ccc}& & \mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{s}\mathit{o}\mathit{p}\mathit{h}\mathit{i}\mathit{c}1-\mathit{f}\mathit{a}\mathit{i}\mathit{l}\mathit{e}\mathit{d}\mathit{S}\mathit{u}\mathit{p}\mathit{e}\mathit{r}\mathit{H}\mathit{y}\mathit{p}\mathit{e}\mathit{r}\mathit{F}\mathit{o}\mathit{r}\mathit{c}\mathit{i}\mathit{n}\mathit{g}=\{\mathit{The}\mathit{number}-\mathit{of}-\mathit{all}\hfill \\ & & -\mathit{the}-\mathit{summation}\hfill \\ & & -\mathit{on}-\mathit{cardinalities}-\mathit{of}-\mathit{SuperHyperParts}-\mathit{minus}-\mathit{two}-\mathit{excerpt}-\mathit{SuperHyperParts}\hfill \\ & & \mathit{SuperHyperSets}\mathit{of}\mathit{the}\mathit{SuperHyperVertices}|min|\mathit{the}\mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}\mathit{with}\mathit{only}\mathit{one}\mathit{exception}\mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\hfill \\ & & \mathit{SuperHyperVertices}\mathit{from}\mathrm{a}\mathit{SuperHyperPart}\mathit{and}\mathit{only}\mathit{one}\mathit{exception}\hfill \\ & & \mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\mathit{SuperHyperVertices}\mathit{from}\mathit{another}\mathit{SuperHyperPart}.\hfill \\ & & {|}_{\mathit{neutrosophic}\mathit{cardinality}\mathit{amid}\mathit{those}\mathit{SuperHyperSets}.}\}\hfill \end{array}$$

where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively.

Proof. 

Assume a connected neutrosophic SuperHyperMultipartite $NSHM:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some neutrosophic numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all neutrosophic number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any 1-failed neutrosophic SuperHyperForcing. Thus, in a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of 1-failed neutrosophic SuperHyperForcing. In other words, here’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices. In a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ the all exterior neutrosophic SuperHyperVertices belong to any 1-failed neutrosophic SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors. Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices with only one exception in the form of interior neutrosophic SuperHyperVertices from a neutrosophic SuperHyperPart and only one exception in the form of interior neutrosophic SuperHyperVertices from another neutrosophic SuperHyperPart. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of all the summation on the neutrosophic cardinality of the all neutrosophic SuperHyperParts minus two excerpt distinct neutrosophic SuperHyperParts. Thus,

$$\begin{array}{ccc}& & \mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{s}\mathit{o}\mathit{p}\mathit{h}\mathit{i}\mathit{c}1-\mathit{f}\mathit{a}\mathit{i}\mathit{l}\mathit{e}\mathit{d}\mathit{S}\mathit{u}\mathit{p}\mathit{e}\mathit{r}\mathit{H}\mathit{y}\mathit{p}\mathit{e}\mathit{r}\mathit{F}\mathit{o}\mathit{r}\mathit{c}\mathit{i}\mathit{n}\mathit{g}=\{\mathit{The}\mathit{number}-\mathit{of}-\mathit{all}\hfill \\ & & -\mathit{the}-\mathit{summation}\hfill \\ & & -\mathit{on}-\mathit{cardinalities}-\mathit{of}-\mathit{SuperHyperParts}-\mathit{minus}-\mathit{two}-\mathit{excerpt}-\mathit{SuperHyperParts}\hfill \\ & & \mathit{SuperHyperSets}\mathit{of}\mathit{the}\mathit{SuperHyperVertices}|min|\mathit{the}\mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}\mathit{with}\mathit{only}\mathit{one}\mathit{exception}\mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\hfill \\ & & \mathit{SuperHyperVertices}\mathit{from}\mathrm{a}\mathit{SuperHyperPart}\mathit{and}\mathit{only}\mathit{one}\mathit{exception}\hfill \\ & & \mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\mathit{SuperHyperVertices}\mathit{from}\mathit{another}\mathit{SuperHyperPart}.\hfill \\ & & {|}_{\mathit{neutrosophic}}\mathit{cardinality}\mathit{amid}\mathit{those}\mathit{SuperHyperSets}.\}\hfill \end{array}$$

where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively. □

Example 42. 

In the Figure (25), the connected neutrosophic SuperHyperMultipartite $NSHM:(V,E),$ is highlighted and featured.

By using the Figure (25) and the Table (8), the neutrosophic SuperHyperMultipartite $NSHM:(V,E),$ is obtained.

The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected neutrosophic SuperHyperMultipartite $NSHM:(V,E),$ in the neutrosophic SuperHyperModel (25), is the 1-failed neutrosophic SuperHyperForcing.

Table 8. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperMultipartite $NSHM:(V,E),$ Mentioned in the Example (42)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 8. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperMultipartite $NSHM:(V,E),$ Mentioned in the Example (42)

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Proposition 43. 

Assume a connected neutrosophic SuperHyperWheel $NSHW:(V,E).$ Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices, excluding the neutrosophic SuperHyperCenter, with only one exception in the form of interior neutrosophic SuperHyperVertices from any given neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of all the neutrosophic number of all the neutrosophic SuperHyperEdges minus two neutrosophic numbers excerpt two neutrosophic SuperHyperNeighbors. Thus,

$$\begin{array}{ccc}& & \mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{s}\mathit{o}\mathit{p}\mathit{h}\mathit{i}\mathit{c}1-\mathit{f}\mathit{a}\mathit{i}\mathit{l}\mathit{e}\mathit{d}\mathit{S}\mathit{u}\mathit{p}\mathit{e}\mathit{r}\mathit{H}\mathit{y}\mathit{p}\mathit{e}\mathit{r}\mathit{F}\mathit{o}\mathit{r}\mathit{c}\mathit{i}\mathit{n}\mathit{g}=\hfill \\ & & \{\mathit{The}\mathit{number}-\mathit{of}-\mathit{all}-\mathit{the}-\mathit{SuperHyperVertices}\hfill \\ & & -\mathit{minus}-\mathit{the}-\mathit{number}-\mathit{of}-\mathit{all}-\mathit{the}-\mathit{SuperHyperEdges}\hfill \\ & & -\mathit{minus}-\mathit{two}-\mathit{numbers}-\mathit{excerpt}-\mathit{two}-\hfill \\ & & \mathit{SuperHyperNeighbors}\mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices}|min|\mathit{the}\mathit{SuperHyperSets}\mathit{of}\mathit{the}\hfill \\ & & \mathit{SuperHyperVertices},\mathit{excluding}\mathit{the}\mathit{SuperHyperCenter}\hfill \\ & & \mathit{with}\mathit{only}\hfill \\ & & \mathit{one}\mathit{exception}\mathit{in}\mathit{the}\mathit{form}\mathit{of}\mathit{interior}\mathit{SuperHyperVertices}\mathit{from}\mathit{any}\mathit{given}\hfill \\ & & {\mathit{SuperHyperEdge}.|}_{\mathit{neutrosophic}\mathit{cardinality}\mathit{amid}\mathit{those}\mathit{SuperHyperSets}.}\}\hfill \end{array}$$

Where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively.

Proof. 

Assume a connected neutrosophic SuperHyperWheel $NSHW:(V,E).$ Let a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices. Consider some neutrosophic numbers of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge excluding three distinct neutrosophic SuperHyperVertices, belong to any given neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices. Consider there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,y,z\}$ is a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t have the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. The neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \left\{x\right\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) but it isn’t an 1-failed neutrosophic SuperHyperForcing. Since it doesn’t do the procedure such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex [there’s at least one white without any white neutrosophic SuperHyperNeighbor outside implying there’s, by the connectedness of the connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ a neutrosophic SuperHyperVertex, titled its neutrosophic SuperHyperNeighbor, to the neutrosophic SuperHyperSet S does the “the color-change rule”.]. There’re only two neutrosophic SuperHyperVertices outside the intended neutrosophic SuperHyperSet, $V\setminus \{x,z\}.$ Thus the obvious 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$ is up. The obvious simple type-neutrosophic SuperHyperSet of the 1-failed neutrosophic SuperHyperForcing, $V\setminus \{x,z\},$is a neutrosophic SuperHyperSet, $V\setminus \{x,z\},$excludes only two neutrosophic SuperHyperVertices are titled in a connected neutrosophic neutrosophic SuperHyperNeighbors neutrosophic SuperHyperGraph $NSHG:(V,E).$ Since the neutrosophic SuperHyperSet of the neutrosophic SuperHyperVertices $V\setminus \{x,z\}$ is the maximum neutrosophic cardinality of a neutrosophic SuperHyperSet S of black neutrosophic SuperHyperVertices (whereas neutrosophic SuperHyperVertices in $V\left(G\right)\setminus S$ are colored white) such that $V\left(G\right)$ isn’t turned black after finitely many applications of “the color-change rule”: a white neutrosophic SuperHyperVertex is converted to a black neutrosophic SuperHyperVertex if it is the only white neutrosophic SuperHyperNeighbor of a black neutrosophic SuperHyperVertex with the additional condition is referred by “1-” about the usage of any black neutrosophic SuperHyperVertex only once to act on white neutrosophic SuperHyperVertex to be black neutrosophic SuperHyperVertex. It implies that neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is $\left|V\right|-2.$ Thus it induces that the neutrosophic number of 1-failed neutrosophic SuperHyperForcing has, the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality, is the neutrosophic cardinality of $V\setminus \{x,z\}$ if there’s an 1-failed neutrosophic SuperHyperForcing with the most neutrosophic cardinality, the upper sharp bound for neutrosophic cardinality. Thus if a neutrosophic SuperHyperEdge has some neutrosophic SuperHyperVertices, then, with excluding two distinct neutrosophic SuperHyperVertices, the all neutrosophic number of those neutrosophic SuperHyperVertices from that neutrosophic SuperHyperEdge belong to any 1-failed neutrosophic SuperHyperForcing. Thus, in a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ there’s a neutrosophic SuperHyperEdge has only two distinct neutrosophic SuperHyperVertices outside of 1-failed neutrosophic SuperHyperForcing. In other words, here’s a neutrosophic SuperHyperEdge has only two distinct white neutrosophic SuperHyperVertices. In a connected neutrosophic neutrosophic SuperHyperGraph $NSHG:(V,E),$ the all exterior neutrosophic SuperHyperVertices belong to any 1-failed neutrosophic SuperHyperForcing if there’s one of them such that there are only two interior neutrosophic SuperHyperVertices are mutually neutrosophic SuperHyperNeighbors. Then an 1-failed neutrosophic SuperHyperForcing is a neutrosophic SuperHyperSet of the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices, excluding the neutrosophic SuperHyperCenter, with only one exception in the form of interior neutrosophic SuperHyperVertices from any given neutrosophic SuperHyperEdge. An 1-failed neutrosophic SuperHyperForcing has the neutrosophic number of all the neutrosophic number of all the neutrosophic SuperHyperEdges minus two neutrosophic numbers excerpt two neutrosophic SuperHyperNeighbors. Thus,

$$\begin{array}{ccc}& & Neutrosophic1-failedSuperHyperForcing=\hfill \\ & & \{\mathrm{The}\mathrm{number}-\mathrm{of}-\mathrm{all}-\mathrm{the}-\mathrm{SuperHyperVertices}\hfill \\ & & -\mathrm{minus}-\mathrm{the}-\mathrm{number}-\mathrm{of}-\mathrm{all}-\mathrm{the}-\mathrm{SuperHyperEdges}\hfill \\ & & -\mathrm{minus}-\mathrm{two}-\mathrm{numbers}-\mathrm{excerpt}-\mathrm{two}-\hfill \\ & & \mathrm{SuperHyperNeighbors}\mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\hfill \\ & & \mathrm{SuperHyperVertices}|min|\mathrm{the}\mathrm{SuperHyperSets}\mathrm{of}\mathrm{the}\hfill \\ & & \mathrm{SuperHyperVertices},\mathrm{excluding}\mathrm{the}\mathrm{SuperHyperCenter}\hfill \\ & & \mathrm{with}\mathrm{only}\hfill \\ & & \mathrm{one}\mathrm{exception}\mathrm{in}\mathrm{the}\mathrm{form}\mathrm{of}\mathrm{interior}\mathrm{SuperHyperVertices}\mathrm{from}\mathrm{any}\mathrm{given}\hfill \\ & & {\mathrm{SuperHyperEdge}.|}_{\mathrm{neutrosophic}\mathrm{cardinality}\mathrm{amid}\mathrm{those}\mathrm{SuperHyperSets}.}\}\hfill \end{array}$$

where ${\sigma }_i$ is the unary operation on the SuperHyperVertices of the SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively. □

Example 44. 

In the Figure (26), the connected neutrosophic SuperHyperWheel $NSHW:(V,E),$ is highlighted and featured.

By using the Figure (26) and the Table (9), the neutrosophic SuperHyperWheel $NSHW:(V,E),$ is obtained.

The obtained neutrosophic SuperHyperSet, by the Algorithm in previous result, of the neutrosophic SuperHyperVertices of the connected neutrosophic SuperHyperWheel $NSHW:(V,E),$ in the neutrosophic SuperHyperModel (26), is the 1-failed neutrosophic SuperHyperForcing.

Table 9. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperWheel $NSHW:(V,E),$ Mentioned in the Example (44).

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

Table 9. The Values of Vertices, SuperVertices, Edges, HyperEdges, and SuperHyperEdges Belong to The Neutrosophic SuperHyperWheel $NSHW:(V,E),$ Mentioned in the Example (44).

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The SuperHyperEdges	The maximum Values of Its Endpoints

4. General Results

For the 1-failed neutrosophic SuperHyperForcing, and the neutrosophic 1-failed neutrosophic SuperHyperForcing, some general results are introduced.

Remark 45. 

Let remind that the neutrosophic 1-failed neutrosophic SuperHyperForcing is “redefined” on the positions of the alphabets.

Corollary 46. 

Assume 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & Neutrosophic1-failedneutrosophicSuperHyperForcing=\hfill \\ & & \{the1-failedneutrosophicSuperHyperForcingoftheneutrosophicSuperHyperVertices|\hfill \\ & & max|neutrosophicSuperHyperDefensiveneutrosophicSuperHyper\hfill \\ & & {Alliances|}_{neutrosophiccardinalityamidthose1-failedneutrosophicSuperHyperForcing.}\}\hfill \end{array}$$

where ${\sigma }_i$ is the unary operation on the neutrosophic SuperHyperVertices of the neutrosophic SuperHyperGraph to assign the determinacy, the indeterminacy and the neutrality, for $i=1,2,3,$ respectively.

Corollary 47. 

Assume a neutrosophic SuperHyperGraph on the same identical letter of the alphabet. Then the notion of neutrosophic 1-failed neutrosophic SuperHyperForcing and 1-failed neutrosophic SuperHyperForcing coincide.

Corollary 48. 

Assume a neutrosophic SuperHyperGraph on the same identical letter of the alphabet. Then a consecutive sequence of the neutrosophic SuperHyperVertices is a neutrosophic 1-failed neutrosophic SuperHyperForcing if and only if it’s an 1-failed neutrosophic SuperHyperForcing.

Corollary 49. 

Assume a neutrosophic SuperHyperGraph on the same identical letter of the alphabet. Then a consecutive sequence of the neutrosophic SuperHyperVertices is a strongest neutrosophic SuperHyperCycle if and only if it’s a longest neutrosophic SuperHyperCycle.

Corollary 50. 

Assume neutrosophic SuperHyperClasses of a neutrosophic SuperHyperGraph on the same identical letter of the alphabet. Then its neutrosophic 1-failed neutrosophic SuperHyperForcing is its 1-failed neutrosophic SuperHyperForcing and reversely.

Corollary 51. 

Assume a neutrosophic SuperHyperPath(-/neutrosophic SuperHyperCycle, neutrosophic SuperHyperStar, neutrosophic SuperHyperBipartite, neutrosophic SuperHyperMultipartite, neutrosophic SuperHyperWheel) on the same identical letter of the alphabet. Then its neutrosophic 1-failed neutrosophic SuperHyperForcing is its 1-failed neutrosophic SuperHyperForcing and reversely.

Corollary 52. 

Assume a neutrosophic SuperHyperGraph. Then its neutrosophic 1-failed neutrosophic SuperHyperForcing isn’t well-defined if and only if its 1-failed neutrosophic SuperHyperForcing isn’t well-defined.

Corollary 53. 

Assume neutrosophic SuperHyperClasses of a neutrosophic SuperHyperGraph. Then its neutrosophic 1-failed neutrosophic SuperHyperForcing isn’t well-defined if and only if its 1-failed neutrosophic SuperHyperForcing isn’t well-defined.

Corollary 54. 

Assume a neutrosophic SuperHyperPath(-/neutrosophic SuperHyperCycle, neutrosophic SuperHyperStar, neutrosophic SuperHyperBipartite, neutrosophic SuperHyperMultipartite, neutrosophic SuperHyperWheel). Then its neutrosophic 1-failed neutrosophic SuperHyperForcing isn’t well-defined if and only if its 1-failed neutrosophic SuperHyperForcing isn’t well-defined.

Corollary 55. 

Assume a neutrosophic SuperHyperGraph. Then its neutrosophic 1-failed neutrosophic SuperHyperForcing is well-defined if and only if its 1-failed neutrosophic SuperHyperForcing is well-defined.

Corollary 56. 

Assume neutrosophic SuperHyperClasses of a neutrosophic SuperHyperGraph. Then its neutrosophic 1-failed neutrosophic SuperHyperForcing is well-defined if and only if its 1-failed neutrosophic SuperHyperForcing is well-defined.

Corollary 57. 

Assume a neutrosophic SuperHyperPath(-/neutrosophic SuperHyperCycle, neutrosophic SuperHyperStar, neutrosophic SuperHyperBipartite, neutrosophic SuperHyperMultipartite, neutrosophic SuperHyperWheel). Then its neutrosophic 1-failed neutrosophic SuperHyperForcing is well-defined if and only if its 1-failed neutrosophic SuperHyperForcing is well-defined.

Proposition 58. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph. Then V is

$\left(i\right):$

the dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

the strong dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

the connected dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

the δ-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

the strong δ-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

the connected δ-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperGraph. Consider $V.$ All neutrosophic SuperHyperMembers of V have at least one neutrosophic SuperHyperNeighbor inside the neutrosophic SuperHyperSet more than neutrosophic SuperHyperNeighbor out of neutrosophic SuperHyperSet. Thus, $\left(i\right).$V is the dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in V,\left|N\right(a)\cap V|>\left|N\right(a)\cap (V\setminus V\left)\right|\equiv \hfill \\ & & \forall a\in V,\left|N\right(a)\cap V|>\left|N\right(a)\cap \varnothing |\equiv \hfill \\ & & \forall a\in V,\left|N\right(a)\cap V|>|\varnothing |\equiv \hfill \\ & & \forall a\in V,\left|N\right(a)\cap V|>0\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(ii\right).$V is the strong dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_s\left(a\right)\cap S|>|N_s\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in V,|N_s\left(a\right)\cap V|>|N_s\left(a\right)\cap (V\setminus V)|\equiv \hfill \\ & & \forall a\in V,|N_s\left(a\right)\cap V|>|N_s\left(a\right)\cap \varnothing |\equiv \hfill \\ & & \forall a\in V,|N_s\left(a\right)\cap V|>|\varnothing |\equiv \hfill \\ & & \forall a\in V,|N_s\left(a\right)\cap V|>0\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(iii\right).$V is the connected dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_c\left(a\right)\cap S|>|N_c\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in V,|N_c\left(a\right)\cap V|>|N_c\left(a\right)\cap (V\setminus V)|\equiv \hfill \\ & & \forall a\in V,|N_c\left(a\right)\cap V|>|N_c\left(a\right)\cap \varnothing |\equiv \hfill \\ & & \forall a\in V,|N_c\left(a\right)\cap V|>|\varnothing |\equiv \hfill \\ & & \forall a\in V,|N_c\left(a\right)\cap V|>0\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(iv\right).$V is the $\delta$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|\right(N\left(a\right)\cap S)-(N\left(a\right)\cap (V\setminus S)\left)\right|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N\left(a\right)\cap V)-(N\left(a\right)\cap (V\setminus V)\left)\right|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N\left(a\right)\cap V)-(N\left(a\right)\cap (\varnothing )\left)\right|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N\left(a\right)\cap V)-(\varnothing \left)\right|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N\left(a\right)\cap V\left)\right|>\delta .\hfill \end{array}$$

$\left(v\right).$V is the strong $\delta$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_s\left(a\right)\cap S)-(N_s\left(a\right)\cap (V\setminus S))|>\delta \equiv \hfill \\ & & \forall a\in V,|(N_s\left(a\right)\cap V)-(N_s\left(a\right)\cap (V\setminus V))|>\delta \equiv \hfill \\ & & \forall a\in V,|(N_s\left(a\right)\cap V)-(N_s\left(a\right)\cap (\varnothing ))|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N_s\left(a\right)\cap V)-(\varnothing )|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N_s\left(a\right)\cap V\left)\right|>\delta .\hfill \end{array}$$

$\left(vi\right).$V is connected $\delta$-dual 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_c\left(a\right)\cap S)-(N_c\left(a\right)\cap (V\setminus S))|>\delta \equiv \hfill \\ & & \forall a\in V,|(N_c\left(a\right)\cap V)-(N_c\left(a\right)\cap (V\setminus V))|>\delta \equiv \hfill \\ & & \forall a\in V,|(N_c\left(a\right)\cap V)-(N_c\left(a\right)\cap (\varnothing ))|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N_c\left(a\right)\cap V)-(\varnothing )|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N_c\left(a\right)\cap V\left)\right|>\delta .\hfill \end{array}$$

□

Proposition 59. 

Let $NTG:(V,E,\sigma ,\mu )$ be a neutrosophic SuperHyperGraph. Then ∅ is

$\left(i\right):$

the neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

the strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

the connected defensive neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

the δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

the strong δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

the connected δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperGraph. Consider $\varnothing .$ All neutrosophic SuperHyperMembers of ∅ have no neutrosophic SuperHyperNeighbor inside the neutrosophic SuperHyperSet less than neutrosophic SuperHyperNeighbor out of neutrosophic SuperHyperSet. Thus,

$\left(i\right).$∅ is the neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in \varnothing ,\left|N\right(a)\cap \varnothing |<\left|N\right(a)\cap (V\setminus \varnothing \left)\right|\equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<\left|N\right(a)\cap (V\setminus \varnothing \left)\right|\equiv \hfill \\ & & \forall a\in \varnothing ,0<\left|N\right(a)\cap V|\equiv \hfill \\ & & \forall a\in \varnothing ,0<\left|N\right(a)\cap V|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(ii\right).$∅ is the strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_s\left(a\right)\cap S|<|N_s\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in \varnothing ,|N_s\left(a\right)\cap \varnothing |<|N_s\left(a\right)\cap (V\setminus \varnothing )|\equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<|N_s\left(a\right)\cap (V\setminus \varnothing )|\equiv \hfill \\ & & \forall a\in \varnothing ,0<|N_s\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in \varnothing ,0<|N_s\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(iii\right).$∅ is the connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_c\left(a\right)\cap S|<|N_c\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in \varnothing ,|N_c\left(a\right)\cap \varnothing |<|N_c\left(a\right)\cap (V\setminus \varnothing )|\equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<|N_c\left(a\right)\cap (V\setminus \varnothing )|\equiv \hfill \\ & & \forall a\in \varnothing ,0<|N_c\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in \varnothing ,0<|N_c\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(iv\right).$∅ is the $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|\right(N\left(a\right)\cap S)-(N\left(a\right)\cap (V\setminus S)\left)\right|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,\left|\right(N\left(a\right)\cap \varnothing )-(N\left(a\right)\cap (V\setminus \varnothing )\left)\right|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,\left|\right(N\left(a\right)\cap \varnothing )-(N\left(a\right)\cap \left(V\right)\left)\right|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

$\left(v\right).$∅ is the strong $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_s\left(a\right)\cap S)-(N_s\left(a\right)\cap (V\setminus S))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|(N_s\left(a\right)\cap \varnothing )-(N_s\left(a\right)\cap (V\setminus \varnothing ))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|(N_s\left(a\right)\cap \varnothing )-(N_s\left(a\right)\cap \left(V\right))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

$\left(vi\right).$∅ is the connected $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_c\left(a\right)\cap S)-(N_c\left(a\right)\cap (V\setminus S))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|(N_c\left(a\right)\cap \varnothing )-(N_c\left(a\right)\cap (V\setminus \varnothing ))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|(N_c\left(a\right)\cap \varnothing )-(N_c\left(a\right)\cap \left(V\right))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

□

Proposition 60. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph. Then an independent neutrosophic SuperHyperSet is

$\left(i\right):$

the neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

the strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

the connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

the δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

the strong δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

the connected δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperGraph. Consider $S.$ All neutrosophic SuperHyperMembers of S have no neutrosophic SuperHyperNeighbor inside the neutrosophic SuperHyperSet less than neutrosophic SuperHyperNeighbor out of neutrosophic SuperHyperSet. Thus,

$\left(i\right).$ An independent neutrosophic SuperHyperSet is the neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,|\varnothing |<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,0<\left|N\right(a)\cap V|\equiv \hfill \\ & & \forall a\in S,0<\left|N\right(a\left)\right|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(ii\right).$ An independent neutrosophic SuperHyperSet is the strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_s\left(a\right)\cap S|<|N_s\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,|N_s\left(a\right)\cap S|<|N_s\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,|\varnothing |<|N_s\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,0<|N_s\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in S,0<|N_s\left(a\right)|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(iii\right).$ An independent neutrosophic SuperHyperSet is the connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_c\left(a\right)\cap S|<|N_c\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,|N_c\left(a\right)\cap S|<|N_c\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,|\varnothing |<|N_c\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,0<|N_c\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in S,0<|N_c\left(a\right)|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

$\left(iv\right).$ An independent neutrosophic SuperHyperSet is the $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|\right(N\left(a\right)\cap S)-(N\left(a\right)\cap (V\setminus S)\left)\right|<\delta \equiv \hfill \\ & & \forall a\in S,\left|\right(N\left(a\right)\cap S)-(N\left(a\right)\cap (V\setminus S)\left)\right|<\delta \equiv \hfill \\ & & \forall a\in S,\left|\right(N\left(a\right)\cap S)-(N\left(a\right)\cap \left(V\right)\left)\right|<\delta \equiv \hfill \\ & & \forall a\in S,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

$\left(v\right).$ An independent neutrosophic SuperHyperSet is the strong $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_s\left(a\right)\cap S)-(N_s\left(a\right)\cap (V\setminus S))|<\delta \equiv \hfill \\ & & \forall a\in S,|(N_s\left(a\right)\cap S)-(N_s\left(a\right)\cap (V\setminus S))|<\delta \equiv \hfill \\ & & \forall a\in S,|(N_s\left(a\right)\cap S)-(N_s\left(a\right)\cap \left(V\right))|<\delta \equiv \hfill \\ & & \forall a\in S,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

$\left(vi\right).$ An independent neutrosophic SuperHyperSet is the connected $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_c\left(a\right)\cap S)-(N_c\left(a\right)\cap (V\setminus S))|<\delta \equiv \hfill \\ & & \forall a\in S,|(N_c\left(a\right)\cap S)-(N_c\left(a\right)\cap (V\setminus S))|<\delta \equiv \hfill \\ & & \forall a\in S,|(N_c\left(a\right)\cap S)-(N_c\left(a\right)\cap \left(V\right))|<\delta \equiv \hfill \\ & & \forall a\in S,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

□

Proposition 61. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperUniform neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperCycle/neutrosophic SuperHyperPath. Then V is a maximal

$\left(i\right):$

neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

$\mathcal{O}\left(NSHG\right)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong $\mathcal{O}\left(NSHG\right)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected $\mathcal{O}\left(NSHG\right)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

Where the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperUniform neutrosophic SuperHyperCycle/neutrosophic SuperHyperPath.

$\left(i\right).$ Consider one segment is out of S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This segment has $2t$ neutrosophic SuperHyperNeighbors in S, i.e, Suppose $x_{i_{i=1,2,\dots ,t}}\in V\setminus S$ such that $y_{i_{i=1,2,\dots ,t}},z_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right).$ By it’s the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide and it’s neutrosophic SuperHyperUniform neutrosophic SuperHyperCycle, $|N\left(x_{i_{i=1,2,\dots ,t}}\right)|=|N\left(y_{i_{i=1,2,\dots ,t}}\right)|=|N\left(z_{i_{i=1,2,\dots ,t}}\right)|=2t.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap S|<\hfill \\ & & |N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap (V\setminus (V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}))|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap S|<\hfill \\ & & |N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap \left\{x_{i_{i=1,2,\dots ,t}}\right\}\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,\left|\{z_1,z_2,\dots ,z_{t-1}\}\right|<\hfill \\ & & \left|\right\{x_1,x_2,\dots ,x_{t-1}\left\}\right)|\equiv \hfill \\ & & \exists y\in S,t-1<t-1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}$ isn’t neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperUniform neutrosophic SuperHyperCycle.

Consider one segment, with two segments related to the neutrosophic SuperHyperLeaves as exceptions, is out of S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This segment has $2t$ neutrosophic SuperHyperNeighbors in S, i.e, Suppose $x_{i_{i=1,2,\dots ,t}}\in V\setminus S$ such that $y_{i_{i=1,2,\dots ,t}},z_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right).$ By it’s the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide and it’s neutrosophic SuperHyperUniform neutrosophic SuperHyperPath, $|N\left(x_{i_{i=1,2,\dots ,t}}\right)|=|N\left(y_{i_{i=1,2,\dots ,t}}\right)|=|N\left(z_{i_{i=1,2,\dots ,t}}\right)|=2t.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap S|<\hfill \\ & & |N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap (V\setminus (V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}))|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap S|<\hfill \\ & & |N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap \left\{x_{i_{i=1,2,\dots ,t}}\right\}\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,\left|\{z_1,z_2,\dots ,z_{t-1}\}\right|<\hfill \\ & & \left|\right\{x_1,x_2,\dots ,x_{t-1}\left\}\right)|\equiv \hfill \\ & & \exists y\in S,t-1<t-1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}$ isn’t neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperUniform neutrosophic SuperHyperPath.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$$\left|V\right|$ is maximal and it’s a neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s $\left|V\right|$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$ □

Proposition 62. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperUniform neutrosophic SuperHyperWheel. Then V is a maximal

$\left(i\right):$

dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

$\mathcal{O}\left(NSHG\right)$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong $\mathcal{O}\left(NSHG\right)$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected $\mathcal{O}\left(NSHG\right)$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

Where the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperUniform neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperWheel.

$\left(i\right).$ Consider one segment is out of S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This segment has $3t$ neutrosophic SuperHyperNeighbors in S, i.e, Suppose $x_{i_{i=1,2,\dots ,t}}\in V\setminus S$ such that $y_{i_{i=1,2,\dots ,t}},z_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right).$ By it’s the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide and it’s neutrosophic SuperHyperUniform neutrosophic SuperHyperWheel, $|N\left(x_{i_{i=1,2,\dots ,t}}\right)|=|N\left(y_{i_{i=1,2,\dots ,t}}\right)|=|N\left(z_{i_{i=1,2,\dots ,t}}\right)|=3t.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right)\in V\setminus {\left\{x_i\right\}}_{i=1}^t,\hfill \\ & & \left|N\right(y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right))\cap S|<\hfill \\ & & |N(y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right))\cap (V\setminus (V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}))|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right)\in V\setminus {\left\{x_i\right\}}_{i=1}^t,\hfill \\ & & \left|N\right(y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right))\cap S|<\hfill \\ & & |N(y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right))\cap \left\{x_{i_{i=1,2,\dots ,t}}\right\}\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right)\in V\setminus {\left\{x_i\right\}}_{i=1}^t,\hfill \\ & & |\{z_1,z_2,\dots ,z_{t-1},z_1^{\prime },z_2^{\prime },\dots ,z_t^{\prime }\}|<|\{x_1,x_2,\dots ,x_{t-1}\}\left)\right|\equiv \hfill \\ & & \exists y\in S,2t-1<t-1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}$ is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperUniform neutrosophic SuperHyperWheel.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$$\left|V\right|$ is maximal and it is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s a dual $\left|V\right|$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$ □

Proposition 63. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperUniform neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperCycle/neutrosophic SuperHyperPath. Then the number of

$\left(i\right):$

the 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

the 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

the connected 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

the $\mathcal{O}\left(NSHG\right)$-1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

the strong $\mathcal{O}\left(NSHG\right)$-1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

the connected $\mathcal{O}\left(NSHG\right)$-1-failed neutrosophic SuperHyperForcing.

is one and it’s only $V.$ Where the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperUniform neutrosophic SuperHyperCycle/neutrosophic SuperHyperPath.

$\left(i\right).$ Consider one segment is out of S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This segment has $2t$ neutrosophic SuperHyperNeighbors in S, i.e, Suppose $x_{i_{i=1,2,\dots ,t}}\in V\setminus S$ such that $y_{i_{i=1,2,\dots ,t}},z_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right).$ By it’s the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide and it’s neutrosophic SuperHyperUniform neutrosophic SuperHyperCycle, $|N\left(x_{i_{i=1,2,\dots ,t}}\right)|=|N\left(y_{i_{i=1,2,\dots ,t}}\right)|=|N\left(z_{i_{i=1,2,\dots ,t}}\right)|=2t.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap S|<\hfill \\ & & |N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap (V\setminus (V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}))|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap S|<\hfill \\ & & |N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap \left\{x_{i_{i=1,2,\dots ,t}}\right\}\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|\{z_1,z_2,\dots ,z_{t-1}\}|<|\{x_1,x_2,\dots ,x_{t-1}\}\left)\right|\equiv \hfill \\ & & \exists y\in S,t-1<t-1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}$ isn’t neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperUniform neutrosophic SuperHyperCycle.

Consider one segment, with two segments related to the neutrosophic SuperHyperLeaves as exceptions, is out of S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This segment has $2t$ neutrosophic SuperHyperNeighbors in S, i.e, Suppose $x_{i_{i=1,2,\dots ,t}}\in V\setminus S$ such that $y_{i_{i=1,2,\dots ,t}},z_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right).$ By it’s the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide and it’s neutrosophic SuperHyperUniform neutrosophic SuperHyperPath, $|N\left(x_{i_{i=1,2,\dots ,t}}\right)|=|N\left(y_{i_{i=1,2,\dots ,t}}\right)|=|N\left(z_{i_{i=1,2,\dots ,t}}\right)|=2t.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap S|<\hfill \\ & & |N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap (V\setminus (V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}))|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,|N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap S|<\hfill \\ & & |N\left(y_{i_{i=1,2,\dots ,t}}\right)\cap \left\{x_{i_{i=1,2,\dots ,t}}\right\}\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}}\in V\setminus {\left\{x_i\right\}}_{i=1}^t,\left|\{z_1,z_2,\dots ,z_{t-1}\}\right|<\hfill \\ & & \left|\right\{x_1,x_2,\dots ,x_{t-1}\left\}\right)|\equiv \hfill \\ & & \exists y\in S,t-1<t-1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}$ isn’t neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperUniform neutrosophic SuperHyperPath.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$$\left|V\right|$ is maximal and it’s a neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s $\left|V\right|$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$ □

Proposition 64. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperUniform neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperWheel. Then the number of

$\left(i\right):$

the dual 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

the dual 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

the dual connected 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

the dual $\mathcal{O}\left(NSHG\right)$-1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

the strong dual $\mathcal{O}\left(NSHG\right)$-1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

the connected dual $\mathcal{O}\left(NSHG\right)$-1-failed neutrosophic SuperHyperForcing.

is one and it’s only $V.$ Where the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperUniform neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperWheel.

$\left(i\right).$ Consider one segment is out of S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This segment has $3t$ neutrosophic SuperHyperNeighbors in S, i.e, Suppose $x_{i_{i=1,2,\dots ,t}}\in V\setminus S$ such that $y_{i_{i=1,2,\dots ,t}},z_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right).$ By it’s the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide and it’s neutrosophic SuperHyperUniform neutrosophic SuperHyperWheel, $|N\left(x_{i_{i=1,2,\dots ,t}}\right)|=|N\left(y_{i_{i=1,2,\dots ,t}}\right)|=|N\left(z_{i_{i=1,2,\dots ,t}}\right)|=3t.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right)\in V\setminus {\left\{x_i\right\}}_{i=1}^t,\hfill \\ & & \left|N\right(y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right))\cap S|<\hfill \\ & & |N(y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right))\cap (V\setminus (V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}))|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right)\in V\setminus {\left\{x_i\right\}}_{i=1}^t\hfill \\ & & ,\left|N\right(y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right))\cap S|<\hfill \\ & & |N(y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right))\cap \left\{x_{i_{i=1,2,\dots ,t}}\right\}\left)\right|\equiv \hfill \\ & & \exists y_{i_{i=1,2,\dots ,t}},s_{i_{i=1,2,\dots ,t}}\in N\left(x_{i_{i=1,2,\dots ,t}}\right)\in V\setminus {\left\{x_i\right\}}_{i=1}^t,\hfill \\ & & |\{z_1,z_2,\dots ,z_{t-1},z_1^{\prime },z_2^{\prime },\dots ,z_t^{\prime }\}|<|\{x_1,x_2,\dots ,x_{t-1}\}\left)\right|\equiv \hfill \\ & & \exists y\in S,2t-1<t-1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x_{i_{i=1,2,\dots ,t}}\right\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperUniform neutrosophic SuperHyperWheel.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$$\left|V\right|$ is maximal and it’s a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it isn’t an $\left|V\right|$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$ □

Proposition 65. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperUniform neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperStar/neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite/neutrosophic SuperHyperComplete neutrosophic SuperHyperMultipartite. Then a neutrosophic SuperHyperSet contains [the neutrosophic SuperHyperCenter and] the half of multiplying r with the number of all the neutrosophic SuperHyperEdges plus one of all the neutrosophic SuperHyperVertices is a

$\left(i\right):$

dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

$\frac{\mathcal{O}\left(NSHG\right)}{2}+1$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong $\frac{\mathcal{O}\left(NSHG\right)}{2}+1$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected $\frac{\mathcal{O}\left(NSHG\right)}{2}+1$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has either $\frac{n}{2}$ or one neutrosophic SuperHyperNeighbors in $S.$ If the neutrosophic SuperHyperVertex is non-neutrosophic SuperHyperCenter, then

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,1>0.\hfill \end{array}$$

If the neutrosophic SuperHyperVertex is neutrosophic SuperHyperCenter, then

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperStar.

Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has at most $\frac{n}{2}$ neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\frac{n}{2}>|N\left(a\right)\cap S|>\frac{n}{2}-1>|N\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite which isn’t a neutrosophic SuperHyperStar.

Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing and they’re chosen from different neutrosophic SuperHyperParts, equally or almost equally as possible. A neutrosophic SuperHyperVertex has at most $\frac{n}{2}$ neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\frac{n}{2}>|N\left(a\right)\cap S|>\frac{n}{2}-1>|N\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperMultipartite which is neither a neutrosophic SuperHyperStar nor neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$${\left\{x_i\right\}}_{i=1}^{\frac{\mathcal{O}\left(NSHG\right)}{2}+1}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s $\frac{\mathcal{O}\left(NSHG\right)}{2}+1$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$ □

Proposition 66. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperUniform neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperStar/neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite/neutrosophic SuperHyperComplete neutrosophic SuperHyperMultipartite. Then a neutrosophic SuperHyperSet contains the half of multiplying r with the number of all the neutrosophic SuperHyperEdges plus one of all the neutrosophic SuperHyperVertices in the biggest neutrosophic SuperHyperPart is a

$\left(i\right):$

neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected δ-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Consider the half of multiplying r with the number of all the neutrosophic SuperHyperEdges plus one of all the neutrosophic SuperHyperVertices in the biggest neutrosophic SuperHyperPart are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has either $n-1,1$ or zero neutrosophic SuperHyperNeighbors in $S.$ If the neutrosophic SuperHyperVertex is in $S,$ then

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,0<1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperStar.

Consider the half of multiplying r with the number of all the neutrosophic SuperHyperEdges plus one of all the neutrosophic SuperHyperVertices in the biggest neutrosophic SuperHyperPart are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has no neutrosophic SuperHyperNeighbor in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,0<\delta .\hfill \end{array}$$

Thus it’s proved. It implies every S is a neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite which isn’t a neutrosophic SuperHyperStar.

Consider the half of multiplying r with the number of all the neutrosophic SuperHyperEdges plus one of all the neutrosophic SuperHyperVertices in the biggest neutrosophic SuperHyperPart are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has no neutrosophic SuperHyperNeighbor in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,0<\delta .\hfill \end{array}$$

Thus it’s proved. It implies every S is a neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperMultipartite which is neither a neutrosophic SuperHyperStar nor neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$S is a neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s an $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$ □

Proposition 67. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperUniform neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperStar/neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite/neutrosophic SuperHyperComplete neutrosophic SuperHyperMultipartite. Then Then the number of

$\left(i\right):$

dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

$\frac{\mathcal{O}\left(NSHG\right)}{2}+1$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong $\frac{\mathcal{O}\left(NSHG\right)}{2}+1$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected $\frac{\mathcal{O}\left(NSHG\right)}{2}+1$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

is one and it’s only $S,$ a neutrosophic SuperHyperSet contains [the neutrosophic SuperHyperCenter and] the half of multiplying r with the number of all the neutrosophic SuperHyperEdges plus one of all the neutrosophic SuperHyperVertices. Where the exterior neutrosophic SuperHyperVertices and the interior neutrosophic SuperHyperVertices coincide.

Proof.$\left(i\right).$ Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has either $\frac{n}{2}$ or one neutrosophic SuperHyperNeighbors in $S.$ If the neutrosophic SuperHyperVertex is non-neutrosophic SuperHyperCenter, then

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,1>0.\hfill \end{array}$$

If the neutrosophic SuperHyperVertex is neutrosophic SuperHyperCenter, then

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperStar.

Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has at most $\frac{n}{2}$ neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\frac{n}{2}>|N\left(a\right)\cap S|>\frac{n}{2}-1>|N\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite which isn’t a neutrosophic SuperHyperStar.

Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing and they’re chosen from different neutrosophic SuperHyperParts, equally or almost equally as possible. A neutrosophic SuperHyperVertex has at most $\frac{n}{2}$ neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\frac{n}{2}>|N\left(a\right)\cap S|>\frac{n}{2}-1>|N\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperMultipartite which is neither a neutrosophic SuperHyperStar nor neutrosophic SuperHyperComplete neutrosophic SuperHyperBipartite.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$${\left\{x_i\right\}}_{i=1}^{\frac{\mathcal{O}\left(NSHG\right)}{2}+1}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s $\frac{\mathcal{O}\left(NSHG\right)}{2}+1$-dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$ □

Proposition 68. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph. The number of connected component is $|V-S|$ if there’s a neutrosophic SuperHyperSet which is a dual

$\left(i\right):$

neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong 1-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected 1-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Consider some neutrosophic SuperHyperVertices are out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. These neutrosophic SuperHyperVertex-type have some neutrosophic SuperHyperNeighbors in S but no neutrosophic SuperHyperNeighbor out of $S.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,1>0.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing and number of connected component is $|V-S|.$

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s a dual 1-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$ □

Proposition 69. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph. Then the number is at most $\mathcal{O}\left(NSHG\right)$ and the neutrosophic number is at most ${\mathcal{O}}_n\left(NSHG\right).$

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperGraph. Consider $V.$ All neutrosophic SuperHyperMembers of V have at least one neutrosophic SuperHyperNeighbor inside the neutrosophic SuperHyperSet more than neutrosophic SuperHyperNeighbor out of neutrosophic SuperHyperSet. Thus,

V is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in V,\left|N\right(a)\cap V|>\left|N\right(a)\cap (V\setminus V\left)\right|\equiv \hfill \\ & & \forall a\in V,\left|N\right(a)\cap V|>\left|N\right(a)\cap \varnothing |\equiv \hfill \\ & & \forall a\in V,\left|N\right(a)\cap V|>|\varnothing |\equiv \hfill \\ & & \forall a\in V,\left|N\right(a)\cap V|>0\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

V is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_s\left(a\right)\cap S|>|N_s\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in V,|N_s\left(a\right)\cap V|>|N_s\left(a\right)\cap (V\setminus V)|\equiv \hfill \\ & & \forall a\in V,|N_s\left(a\right)\cap V|>|N_s\left(a\right)\cap \varnothing |\equiv \hfill \\ & & \forall a\in V,|N_s\left(a\right)\cap V|>|\varnothing |\equiv \hfill \\ & & \forall a\in V,|N_s\left(a\right)\cap V|>0\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

V is connected a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_c\left(a\right)\cap S|>|N_c\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in V,|N_c\left(a\right)\cap V|>|N_c\left(a\right)\cap (V\setminus V)|\equiv \hfill \\ & & \forall a\in V,|N_c\left(a\right)\cap V|>|N_c\left(a\right)\cap \varnothing |\equiv \hfill \\ & & \forall a\in V,|N_c\left(a\right)\cap V|>|\varnothing |\equiv \hfill \\ & & \forall a\in V,|N_c\left(a\right)\cap V|>0\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

V is a dual $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|\right(N\left(a\right)\cap S)-(N\left(a\right)\cap (V\setminus S)\left)\right|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N\left(a\right)\cap V)-(N\left(a\right)\cap (V\setminus V)\left)\right|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N\left(a\right)\cap V)-(N\left(a\right)\cap (\varnothing )\left)\right|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N\left(a\right)\cap V)-(\varnothing \left)\right|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N\left(a\right)\cap V\left)\right|>\delta .\hfill \end{array}$$

V is a dual strong $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_s\left(a\right)\cap S)-(N_s\left(a\right)\cap (V\setminus S))|>\delta \equiv \hfill \\ & & \forall a\in V,|(N_s\left(a\right)\cap V)-(N_s\left(a\right)\cap (V\setminus V))|>\delta \equiv \hfill \\ & & \forall a\in V,|(N_s\left(a\right)\cap V)-(N_s\left(a\right)\cap (\varnothing ))|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N_s\left(a\right)\cap V)-(\varnothing )|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N_s\left(a\right)\cap V\left)\right|>\delta .\hfill \end{array}$$

V is a dual connected $\delta$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_c\left(a\right)\cap S)-(N_c\left(a\right)\cap (V\setminus S))|>\delta \equiv \hfill \\ & & \forall a\in V,|(N_c\left(a\right)\cap V)-(N_c\left(a\right)\cap (V\setminus V))|>\delta \equiv \hfill \\ & & \forall a\in V,|(N_c\left(a\right)\cap V)-(N_c\left(a\right)\cap (\varnothing ))|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N_c\left(a\right)\cap V)-(\varnothing )|>\delta \equiv \hfill \\ & & \forall a\in V,\left|\right(N_c\left(a\right)\cap V\left)\right|>\delta .\hfill \end{array}$$

Thus V is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing and V is the biggest neutrosophic SuperHyperSet in $NSHG:(V,E).$ Then the number is at most $\mathcal{O}(NSHG:(V,E\left)\right)$ and the neutrosophic number is at most ${\mathcal{O}}_n(NSHG:(V,E)).$ □

Proposition 70. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph which is neutrosophic SuperHyperComplete. The number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of dual

$\left(i\right):$

neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

$(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Consider n half $-1$ neutrosophic SuperHyperVertices are out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has n half neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperGraph. Thus the number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right).$ Consider n half $-1$ neutrosophic SuperHyperVertices are out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has n half neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperGraph. Thus the number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of a dual strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iii\right).$ Consider n half $-1$ neutrosophic SuperHyperVertices are out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has n half neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperGraph. Thus the number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of a dual connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iv\right).$ Consider n half $-1$ neutrosophic SuperHyperVertices are out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has n half neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperGraph. Thus the number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of a dual $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right).$ Consider n half $-1$ neutrosophic SuperHyperVertices are out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has n half neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual strong $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperGraph. Thus the number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of a dual strong $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(vi\right).$ Consider n half $-1$ neutrosophic SuperHyperVertices are out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has n half neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual connected $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperComplete neutrosophic SuperHyperGraph. Thus the number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of a dual connected $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 71. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph which is $\varnothing .$ The number is 0 and the neutrosophic number is $0,$ for an independent neutrosophic SuperHyperSet in the setting of dual

$\left(i\right):$

neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

0-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong 0-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected 0-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperGraph. Consider $\varnothing .$ All neutrosophic SuperHyperMembers of ∅ have no neutrosophic SuperHyperNeighbor inside the neutrosophic SuperHyperSet less than neutrosophic SuperHyperNeighbor out of neutrosophic SuperHyperSet. Thus,

$\left(i\right).$∅ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in \varnothing ,\left|N\right(a)\cap \varnothing |<\left|N\right(a)\cap (V\setminus \varnothing \left)\right|\equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<\left|N\right(a)\cap (V\setminus \varnothing \left)\right|\equiv \hfill \\ & & \forall a\in \varnothing ,0<\left|N\right(a)\cap V|\equiv \hfill \\ & & \forall a\in \varnothing ,0<\left|N\right(a)\cap V|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

The number is 0 and the neutrosophic number is $0,$ for an independent neutrosophic SuperHyperSet in the setting of a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right).$∅ is a dual strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_s\left(a\right)\cap S|<|N_s\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in \varnothing ,|N_s\left(a\right)\cap \varnothing |<|N_s\left(a\right)\cap (V\setminus \varnothing )|\equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<|N_s\left(a\right)\cap (V\setminus \varnothing )|\equiv \hfill \\ & & \forall a\in \varnothing ,0<|N_s\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in \varnothing ,0<|N_s\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

The number is 0 and the neutrosophic number is $0,$ for an independent neutrosophic SuperHyperSet in the setting of a dual strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iii\right).$∅ is a dual connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|N_c\left(a\right)\cap S|<|N_c\left(a\right)\cap (V\setminus S)|\equiv \hfill \\ & & \forall a\in \varnothing ,|N_c\left(a\right)\cap \varnothing |<|N_c\left(a\right)\cap (V\setminus \varnothing )|\equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<|N_c\left(a\right)\cap (V\setminus \varnothing )|\equiv \hfill \\ & & \forall a\in \varnothing ,0<|N_c\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in \varnothing ,0<|N_c\left(a\right)\cap V|\equiv \hfill \\ & & \forall a\in V,\delta >0.\hfill \end{array}$$

The number is 0 and the neutrosophic number is $0,$ for an independent neutrosophic SuperHyperSet in the setting of a dual connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iv\right).$∅ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,\left|\right(N\left(a\right)\cap S)-(N\left(a\right)\cap (V\setminus S)\left)\right|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,\left|\right(N\left(a\right)\cap \varnothing )-(N\left(a\right)\cap (V\setminus \varnothing )\left)\right|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,\left|\right(N\left(a\right)\cap \varnothing )-(N\left(a\right)\cap \left(V\right)\left)\right|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

The number is 0 and the neutrosophic number is $0,$ for an independent neutrosophic SuperHyperSet in the setting of a dual 0-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right).$∅ is a dual strong 0-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_s\left(a\right)\cap S)-(N_s\left(a\right)\cap (V\setminus S))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|(N_s\left(a\right)\cap \varnothing )-(N_s\left(a\right)\cap (V\setminus \varnothing ))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|(N_s\left(a\right)\cap \varnothing )-(N_s\left(a\right)\cap \left(V\right))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

The number is 0 and the neutrosophic number is $0,$ for an independent neutrosophic SuperHyperSet in the setting of a dual strong 0-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(vi\right).$∅ is a dual connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing since the following statements are equivalent.

$$\begin{array}{ccc}& & \forall a\in S,|(N_c\left(a\right)\cap S)-(N_c\left(a\right)\cap (V\setminus S))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|(N_c\left(a\right)\cap \varnothing )-(N_c\left(a\right)\cap (V\setminus \varnothing ))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|(N_c\left(a\right)\cap \varnothing )-(N_c\left(a\right)\cap \left(V\right))|<\delta \equiv \hfill \\ & & \forall a\in \varnothing ,|\varnothing |<\delta \equiv \hfill \\ & & \forall a\in V,0<\delta .\hfill \end{array}$$

The number is 0 and the neutrosophic number is $0,$ for an independent neutrosophic SuperHyperSet in the setting of a dual connected 0-offensive neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 72. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph which is neutrosophic SuperHyperComplete. Then there’s no independent neutrosophic SuperHyperSet.

Proposition 73. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph which is neutrosophic SuperHyperCycle/neutrosophic SuperHyperPath/neutrosophic SuperHyperWheel. The number is $\mathcal{O}(NSHG:(V,E\left)\right)$ and the neutrosophic number is ${\mathcal{O}}_n(NSHG:(V,E)),$ in the setting of a dual

$\left(i\right):$

neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

$\mathcal{O}(NSHG:(V,E\left)\right)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong $\mathcal{O}(NSHG:(V,E\left)\right)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected $\mathcal{O}(NSHG:(V,E\left)\right)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof. 

Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperGraph which is neutrosophic SuperHyperCycle/neutrosophic SuperHyperPath/neutrosophic SuperHyperWheel.

$\left(i\right).$ Consider one neutrosophic SuperHyperVertex is out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This neutrosophic SuperHyperVertex has one neutrosophic SuperHyperNeighbor in S, i.e, suppose $x\in V\setminus S$ such that $y,z\in N\left(x\right).$ By it’s neutrosophic SuperHyperCycle, $\left|N\right(x\left)\right|=\left|N\right(y\left)\right|=\left|N\right(z\left)\right|=2.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|N\right(y)\cap S|<\left|N\right(y)\cap (V\setminus (V\setminus \{x\left\}\right)\left)\right|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|N\right(y)\cap S|<\left|N\right(y)\cap \{x\left\}\right)|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|\right\{z\left\}\right|<\left|\right\{x\left\}\right)|\equiv \hfill \\ & & \exists y\in S,1<1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x\right\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperCycle.

Consider one neutrosophic SuperHyperVertex is out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This neutrosophic SuperHyperVertex has one neutrosophic SuperHyperNeighbor in S, i.e, Suppose $x\in V\setminus S$ such that $y,z\in N\left(x\right).$ By it’s neutrosophic SuperHyperPath, $\left|N\right(x\left)\right|=\left|N\right(y\left)\right|=\left|N\right(z\left)\right|=2.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|N\right(y)\cap S|<\left|N\right(y)\cap (V\setminus (V\setminus \{x\left\}\right)\left)\right|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|N\right(y)\cap S|<\left|N\right(y)\cap \{x\left\}\right)|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|\right\{z\left\}\right|<\left|\right\{x\left\}\right)|\equiv \hfill \\ & & \exists y\in S,1<1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x\right\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperPath.

Consider one neutrosophic SuperHyperVertex is out of S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. This neutrosophic SuperHyperVertex has one neutrosophic SuperHyperNeighbor in S, i.e, Suppose $x\in V\setminus S$ such that $y,z\in N\left(x\right).$ By it’s neutrosophic SuperHyperWheel, $\left|N\right(x\left)\right|=\left|N\right(y\left)\right|=\left|N\right(z\left)\right|=2.$ Thus

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\left|N\right(a)\cap S|<\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|N\right(y)\cap S|<\left|N\right(y)\cap (V\setminus (V\setminus \{x\left\}\right)\left)\right|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|N\right(y)\cap S|<\left|N\right(y)\cap \{x\left\}\right)|\equiv \hfill \\ & & \exists y\in V\setminus \left\{x\right\},\left|\right\{z\left\}\right|<\left|\right\{x\left\}\right)|\equiv \hfill \\ & & \exists y\in S,1<1.\hfill \end{array}$$

Thus it’s contradiction. It implies every $V\setminus \left\{x\right\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperWheel.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$V is maximal and it’s a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s a dual $\mathcal{O}(NSHG:(V,E\left)\right)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$

Thus the number is $\mathcal{O}(NSHG:(V,E\left)\right)$ and the neutrosophic number is ${\mathcal{O}}_n(NSHG:(V,E)),$ in the setting of all types of a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 74. 

Let $NSHG:(V,E)$ be a neutrosophic SuperHyperGraph which is neutrosophic SuperHyperStar/complete neutrosophic SuperHyperBipartite/complete neutrosophic SuperHyperMultiPartite. The number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of a dual

$\left(i\right):$

neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right):$

strong neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right):$

connected neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right):$

$(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(v\right):$

strong $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(vi\right):$

connected $(\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. A neutrosophic SuperHyperVertex has at most n half neutrosophic SuperHyperNeighbors in $S.$ If the neutrosophic SuperHyperVertex is the non-neutrosophic SuperHyperCenter, then

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,1>0.\hfill \end{array}$$

If the neutrosophic SuperHyperVertex is the neutrosophic SuperHyperCenter, then

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{n}{2}>\frac{n}{2}-1.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given neutrosophic SuperHyperStar.

Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{\delta }{2}>n-\frac{\delta }{2}.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given complete neutrosophic SuperHyperBipartite which isn’t a neutrosophic SuperHyperStar.

Consider n half $+1$ neutrosophic SuperHyperVertices are in S which is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing and they are chosen from different neutrosophic SuperHyperParts, equally or almost equally as possible. A neutrosophic SuperHyperVertex in S has $\delta$ half neutrosophic SuperHyperNeighbors in $S.$

$$\begin{array}{ccc}& & \forall a\in S,\left|N\right(a)\cap S|>\left|N\right(a)\cap (V\setminus S\left)\right|\equiv \hfill \\ & & \forall a\in S,\frac{\delta }{2}>n-\frac{\delta }{2}.\hfill \end{array}$$

Thus it’s proved. It implies every S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing in a given complete neutrosophic SuperHyperMultipartite which is neither a neutrosophic SuperHyperStar nor complete neutrosophic SuperHyperBipartite.

$\left(ii\right),$$\left(iii\right)$ are obvious by $\left(i\right).$

$\left(iv\right).$ By $\left(i\right),$${\left\{x_i\right\}}_{i=1}^{\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1}$ is maximal and it’s a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s a dual $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(v\right),\left(vi\right)$ are obvious by $\left(iv\right).$

Thus the number is $\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}+1$ and the neutrosophic number is $min{\Sigma }_{v\in {\{v_1,v_2,\cdots ,v_t\}}_{t>\frac{\mathcal{O}(NSHG:(V,E\left)\right)}{2}}\subseteq V}\sigma \left(v\right),$ in the setting of all dual 1-failed neutrosophic SuperHyperForcing. □

Proposition 75. 

Let $\mathcal{NSHF}:(V,E)$ be a neutrosophic SuperHyperFamily of the $NSHGs:(V,E)$ neutrosophic SuperHyperGraphs which are from one-type neutrosophic SuperHyperClass which the result is obtained for the individuals. Then the results also hold for the neutrosophic SuperHyperFamily $\mathcal{NSHF}:(V,E)$ of these specific neutrosophic SuperHyperClasses of the neutrosophic SuperHyperGraphs.

Proof. 

There are neither neutrosophic SuperHyperConditions nor neutrosophic SuperHyperRestrictions on the neutrosophic SuperHyperVertices. Thus the neutrosophic SuperHyperResults on individuals, $NSHGs:(V,E),$ are extended to the neutrosophic SuperHyperResults on neutrosophic SuperHyperFamily, $\mathcal{NSHF}:(V,E).$ □

Proposition 76. 

Let $NSHG:(V,E)$ be a strong neutrosophic SuperHyperGraph. If S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, then $\forall v\in V\setminus S,\exists x\in S$ such that

$\left(i\right)$

$v\in N_s\left(x\right);$

$\left(ii\right)$

$vx\in E.$

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Consider $v\in V\setminus S.$ Since S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing,

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,|N_s\left(v\right)\cap S|>|N_s\left(v\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,\exists x\in S,v\in N_s\left(x\right).\hfill \end{array}$$

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Consider $v\in V\setminus S.$ Since S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing,

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,|N_s\left(v\right)\cap S|>|N_s\left(v\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,\exists x\in S:v\in N_s\left(x\right)\hfill \\ & & v\in V\setminus S,\exists x\in S:vx\in E,\mu \left(vx\right)=\sigma \left(v\right)\wedge \sigma \left(x\right).\hfill \\ & & v\in V\setminus S,\exists x\in S:vx\in E.\hfill \end{array}$$

□

Proposition 77. 

Let $NSHG:(V,E)$ be a strong neutrosophic SuperHyperGraph. If S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, then

$\left(i\right)$

S is neutrosophic SuperHyperDominating set;

$\left(ii\right)$

there’s $S\subseteq S^{\prime }$ such that $|S^{\prime }|$ is neutrosophic SuperHyperChromatic number.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Consider $v\in V\setminus S.$ Since S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, either

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,|N_s\left(v\right)\cap S|>|N_s\left(v\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,\exists x\in S,v\in N_s\left(x\right)\hfill \end{array}$$

or

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,|N_s\left(v\right)\cap S|>|N_s\left(v\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,\exists x\in S:v\in N_s\left(x\right)\hfill \\ & & v\in V\setminus S,\exists x\in S:vx\in E,\mu \left(vx\right)=\sigma \left(v\right)\wedge \sigma \left(x\right)\hfill \\ & & v\in V\setminus S,\exists x\in S:vx\in E.\hfill \end{array}$$

It implies S is neutrosophic SuperHyperDominating neutrosophic SuperHyperSet.

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Consider $v\in V\setminus S.$ Since S is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, either

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,|N_s\left(v\right)\cap S|>|N_s\left(v\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,\exists x\in S,v\in N_s\left(x\right)\hfill \end{array}$$

or

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,|N_s\left(v\right)\cap S|>|N_s\left(v\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus S,\exists x\in S:v\in N_s\left(x\right)\hfill \\ & & v\in V\setminus S,\exists x\in S:vx\in E,\mu \left(vx\right)=\sigma \left(v\right)\wedge \sigma \left(x\right)\hfill \\ & & v\in V\setminus S,\exists x\in S:vx\in E.\hfill \end{array}$$

Thus every neutrosophic SuperHyperVertex $v\in V\setminus S,$ has at least one neutrosophic SuperHyperNeighbor in $S.$ The only case is about the relation amid neutrosophic SuperHyperVertices in S in the terms of neutrosophic SuperHyperNeighbors. It implies there’s $S\subseteq S^{\prime }$ such that $|S^{\prime }|$ is neutrosophic SuperHyperChromatic number. □

Proposition 78. 

Let $NSHG:(V,E)$ be a strong neutrosophic SuperHyperGraph. Then

$\left(i\right)$

$\Gamma \le \mathcal{O};$

$\left(ii\right)$

${\Gamma }_s\le {\mathcal{O}}_n.$

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Let $S=V.$

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus V,|N_s\left(v\right)\cap V|>|N_s\left(v\right)\cap (V\setminus V)|\hfill \\ & & v\in \varnothing ,|N_s\left(v\right)\cap V|>|N_s\left(v\right)\cap \varnothing |\hfill \\ & & v\in \varnothing ,|N_s\left(v\right)\cap V|>|\varnothing |\hfill \\ & & v\in \varnothing ,|N_s\left(v\right)\cap V|>0\hfill \end{array}$$

It implies V is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. For all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,S\subseteq V.$ Thus for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,\left|S\right|\le \left|V\right|.$ It implies for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,\left|S\right|\le \mathcal{O}.$ So for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,\Gamma \le \mathcal{O}.$

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Let $S=V.$

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus V,|N_s\left(v\right)\cap V|>|N_s\left(v\right)\cap (V\setminus V)|\hfill \\ & & v\in \varnothing ,|N_s\left(v\right)\cap V|>|N_s\left(v\right)\cap \varnothing |\hfill \\ & & v\in \varnothing ,|N_s\left(v\right)\cap V|>|\varnothing |\hfill \\ & & v\in \varnothing ,|N_s\left(v\right)\cap V|>0\hfill \end{array}$$

It implies V is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. For all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,S\subseteq V.$ Thus for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,{\Sigma }_{s\in S}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\le {\Sigma }_{v\in V}{\Sigma }_{i=1}^3{\sigma }_i\left(v\right).$ It implies for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,{\Sigma }_{s\in S}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\le {\mathcal{O}}_n.$ So for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,{\Gamma }_s\le {\mathcal{O}}_n.$ □

Proposition 79. 

Let $NSHG:(V,E)$ be a strong neutrosophic SuperHyperGraph which is connected. Then

$\left(i\right)$

$\Gamma \le \mathcal{O}-1;$

$\left(ii\right)$

${\Gamma }_s\le {\mathcal{O}}_n-{\Sigma }_{i=1}^3{\sigma }_i\left(x\right).$

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Let $S=V-\left\{x\right\}$ where x is arbitrary and $x\in V.$

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus V-\left\{x\right\},|N_s\left(v\right)\cap (V-\left\{x\right\})|>|N_s\left(v\right)\cap (V\setminus (V-\left\{x\right\}))|\hfill \\ & & |N_s\left(x\right)\cap (V-\left\{x\right\})|>|N_s\left(x\right)\cap \left\{x\right\}|\hfill \\ & & |N_s\left(x\right)\cap (V-\left\{x\right\})|>|\varnothing |\hfill \\ & & |N_s\left(x\right)\cap (V-\left\{x\right\})|>0\hfill \end{array}$$

It implies $V-\left\{x\right\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. For all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S\ne V,S\subseteq V-\left\{x\right\}.$ Thus for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S\ne V,\left|S\right|\le |V-\{x\left\}\right|.$ It implies for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S\ne V,\left|S\right|\le \mathcal{O}-1.$ So for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,\Gamma \le \mathcal{O}-1.$

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Let $S=V-\left\{x\right\}$ where x is arbitrary and $x\in V.$

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus V-\left\{x\right\},|N_s\left(v\right)\cap (V-\left\{x\right\})|>|N_s\left(v\right)\cap (V\setminus (V-\left\{x\right\}))|\hfill \\ & & |N_s\left(x\right)\cap (V-\left\{x\right\})|>|N_s\left(x\right)\cap \left\{x\right\}|\hfill \\ & & |N_s\left(x\right)\cap (V-\left\{x\right\})|>|\varnothing |\hfill \\ & & |N_s\left(x\right)\cap (V-\left\{x\right\})|>0\hfill \end{array}$$

It implies $V-\left\{x\right\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. For all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S\ne V,S\subseteq V-\left\{x\right\}.$ Thus for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S\ne V,{\Sigma }_{s\in S}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\le {\Sigma }_{v\in V-\left\{x\right\}}{\Sigma }_{i=1}^3{\sigma }_i\left(v\right).$ It implies for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S\ne V,{\Sigma }_{s\in S}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\le {\mathcal{O}}_n-{\Sigma }_{i=1}^3{\sigma }_i\left(x\right).$ So for all neutrosophic SuperHyperSets of neutrosophic SuperHyperVertices $S,{\Gamma }_s\le {\mathcal{O}}_n-{\Sigma }_{i=1}^3{\sigma }_i\left(x\right).$ □

Proposition 80. 

Let $NSHG:(V,E)$ be an odd neutrosophic SuperHyperPath. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S=\{v_2,v_4,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\Gamma =\lfloor \frac{n}{2}\rfloor +1$ and corresponded neutrosophic SuperHyperSet is $S=\{v_2,v_4,\cdots ,v_{n-1}\}$;

$\left(iii\right)$

${\Gamma }_s=min\{{\Sigma }_{s\in S=\{v_2,v_4,\cdots ,v_{n-1}\}}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right),{\Sigma }_{s\in S=\{v_1,v_3,\cdots ,v_{n-1}\}}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\};$

$\left(iv\right)$

the neutrosophic SuperHyperSets $S_1=\{v_2,v_4,\cdots ,v_{n-1}\}$ and $S_2=\{v_1,v_3,\cdots ,v_{n-1}\}$ are only a dual 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is an odd neutrosophic SuperHyperPath. Let $S=\{v_2,v_4,\cdots ,v_{n-1}\}$ where for all $v_i,v_j\in \{v_2,v_4,\cdots ,v_{n-1}\},v_i{v}_j\notin E$ and $v_i,v_j\in V.$

$$\begin{array}{ccc}& & v\in \{v_1,v_3,\cdots ,v_n\},|N_s\left(v\right)\cap \{v_2,v_4,\cdots .v_{n-1}\}|=2>\hfill \\ & & 0=|N_s\left(v\right)\cap \{v_1,v_3,\cdots ,v_n\}|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>\hfill \\ & & 0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \{v_2,v_4,\cdots ,v_{n-1}\},|N_s\left(v\right)\cap \{v_2,v_4,\cdots .v_{n-1}\}|>\hfill \\ & & |N_s\left(v\right)\cap (V\setminus \{v_2,v_4,\cdots .v_{n-1}\})|\hfill \end{array}$$

It implies $S=\{v_2,v_4,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\{v_2,v_4,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_2,v_4,\cdots ,v_{n-1}\},$ then

$$\begin{array}{ccc}& & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1=1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1\neg >1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $\{v_2,v_4,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_2,v_4,\cdots ,v_{n-1}\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_2,v_4,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right)$ and $\left(iii\right)$ are trivial.

$\left(iv\right).$ By $\left(i\right),$$S_1=\{v_2,v_4,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s enough to show that $S_2=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Suppose $NSHG:(V,E)$ is an odd neutrosophic SuperHyperPath. Let $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ where for all $v_i,v_j\in \{v_1,v_3,\cdots ,v_{n-1}\},v_i{v}_j\notin E$ and $v_i,v_j\in V.$

$$\begin{array}{ccc}& & v\in \{v_2,v_4,\cdots ,v_n\},|N_s\left(v\right)\cap \{v_1,v_3,\cdots .v_{n-1}\}|=2>\hfill \\ & & 0=|N_s\left(v\right)\cap \{v_2,v_4,\cdots ,v_n\}|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \{v_1,v_3,\cdots ,v_{n-1}\},|N_s\left(v\right)\cap \{v_1,v_3,\cdots .v_{n-1}\}|>\hfill \\ & & |N_s\left(v\right)\cap (V\setminus \{v_1,v_3,\cdots .v_{n-1}\})|\hfill \end{array}$$

It implies $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\{v_1,v_3,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_1,v_3,\cdots ,v_{n-1}\},$ then

$$\begin{array}{ccc}& & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1=1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1\neg >1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $\{v_1,v_3,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_1,v_3,\cdots ,v_{n-1}\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 81. 

Let $NSHG:(V,E)$ be an even neutrosophic SuperHyperPath. Then

$\left(i\right)$

the set $S=\{v_2,v_4,\cdots .v_n\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\Gamma =\lfloor \frac{n}{2}\rfloor$ and corresponded neutrosophic SuperHyperSets are $\{v_2,v_4,\cdots .v_n\}$ and $\{v_1,v_3,\cdots .v_{n-1}\};$

$\left(iii\right)$

${\Gamma }_s=min\{{\Sigma }_{s\in S=\{v_2,v_4,\cdots ,v_n\}}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right),{\Sigma }_{s\in S=\{v_1,v_3,\cdots .v_{n-1}\}}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\};$

$\left(iv\right)$

the neutrosophic SuperHyperSets $S_1=\{v_2,v_4,\cdots .v_n\}$ and $S_2=\{v_1,v_3,\cdots .v_{n-1}\}$ are only dual 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is an even neutrosophic SuperHyperPath. Let $S=\{v_2,v_4,\cdots ,v_n\}$ where for all $v_i,v_j\in \{v_2,v_4,\cdots ,v_n\},v_i{v}_j\notin E$ and $v_i,v_j\in V.$

$$\begin{array}{ccc}& & v\in \{v_1,v_3,\cdots ,v_{n-1}\},|N_s\left(v\right)\cap \{v_2,v_4,\cdots .v_n\}|=2>\hfill \\ & & 0=|N_s\left(v\right)\cap \{v_1,v_3,\cdots ,v_{n-1}\}|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>\hfill \\ & & 0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \{v_2,v_4,\cdots ,v_n\},|N_s\left(v\right)\cap \{v_2,v_4,\cdots .v_n\}|>|N_s\left(v\right)\cap (V\setminus \{v_2,v_4,\cdots .v_n\})|\hfill \end{array}$$

It implies $S=\{v_2,v_4,\cdots ,v_n\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\{v_2,v_4,\cdots ,v_n\}-\left\{v_i\right\}$ where $v_i\in \{v_2,v_4,\cdots ,v_n\},$ then

$$\begin{array}{ccc}& & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1=1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1\neg >1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $\{v_2,v_4,\cdots ,v_n\}-\left\{v_i\right\}$ where $v_i\in \{v_2,v_4,\cdots ,v_n\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_2,v_4,\cdots ,v_n\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right)$ and $\left(iii\right)$ are trivial.

$\left(iv\right).$ By $\left(i\right),$$S_1=\{v_2,v_4,\cdots ,v_n\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s enough to show that $S_2=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Suppose $NSHG:(V,E)$ is an even neutrosophic SuperHyperPath. Let $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ where for all $v_i,v_j\in \{v_1,v_3,\cdots ,v_{n-1}\},v_i{v}_j\notin E$ and $v_i,v_j\in V.$

$$\begin{array}{ccc}& & v\in \{v_2,v_4,\cdots ,v_n\},|N_s\left(v\right)\cap \{v_1,v_3,\cdots .v_{n-1}\}|=2>\hfill \\ & & 0=|N_s\left(v\right)\cap \{v_2,v_4,\cdots ,v_n\}|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \{v_1,v_3,\cdots ,v_{n-1}\},|N_s\left(v\right)\cap \{v_1,v_3,\cdots .v_{n-1}\}|>\hfill \\ & & |N_s\left(v\right)\cap (V\setminus \{v_1,v_3,\cdots .v_{n-1}\})|\hfill \end{array}$$

It implies $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\{v_1,v_3,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_1,v_3,\cdots ,v_{n-1}\},$ then

$$\begin{array}{ccc}& & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1=1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1\neg >1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $\{v_1,v_3,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_1,v_3,\cdots ,v_{n-1}\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 82. 

Let $NSHG:(V,E)$ be an even neutrosophic SuperHyperCycle. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S=\{v_2,v_4,\cdots ,v_n\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\Gamma =\lfloor \frac{n}{2}\rfloor$ and corresponded neutrosophic SuperHyperSets are $\{v_2,v_4,\cdots ,v_n\}$ and $\{v_1,v_3,\cdots ,v_{n-1}\};$

$\left(iii\right)$

${\Gamma }_s=min\{{\Sigma }_{s\in S=\{v_2,v_4,\cdots ,v_n\}}\sigma \left(s\right),{\Sigma }_{s\in S=\{v_1,v_3,\cdots ,v_{n-1}\}}\sigma \left(s\right)\};$

$\left(iv\right)$

the neutrosophic SuperHyperSets $S_1=\{v_2,v_4,\cdots ,v_n\}$ and $S_2=\{v_1,v_3,\cdots ,v_{n-1}\}$ are only dual 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is an even neutrosophic SuperHyperCycle. Let $S=\{v_2,v_4,\cdots ,v_n\}$ where for all $v_i,v_j\in \{v_2,v_4,\cdots ,v_n\},v_i{v}_j\notin E$ and $v_i,v_j\in V.$

$$\begin{array}{ccc}& & v\in \{v_1,v_3,\cdots ,v_{n-1}\},|N_s\left(v\right)\cap \{v_2,v_4,\cdots .v_n\}|=2>\hfill \\ & & 0=|N_s\left(v\right)\cap \{v_1,v_3,\cdots ,v_{n-1}\}|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>\hfill \\ & & 0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \{v_2,v_4,\cdots ,v_n\},|N_s\left(v\right)\cap \{v_2,v_4,\cdots .v_n\}|>\hfill \\ & & |N_s\left(v\right)\cap (V\setminus \{v_2,v_4,\cdots .v_n\})|\hfill \end{array}$$

It implies $S=\{v_2,v_4,\cdots ,v_n\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\{v_2,v_4,\cdots ,v_n\}-\left\{v_i\right\}$ where $v_i\in \{v_2,v_4,\cdots ,v_n\},$ then

$$\begin{array}{ccc}& & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1=1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1\neg >1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $\{v_2,v_4,\cdots ,v_n\}-\left\{v_i\right\}$ where $v_i\in \{v_2,v_4,\cdots ,v_n\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_2,v_4,\cdots ,v_n\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right)$ and $\left(iii\right)$ are trivial.

$\left(iv\right).$ By $\left(i\right),$$S_1=\{v_2,v_4,\cdots ,v_n\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s enough to show that $S_2=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Suppose $NSHG:(V,E)$ is an even neutrosophic SuperHyperCycle. Let $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ where for all $v_i,v_j\in \{v_1,v_3,\cdots ,v_{n-1}\},v_i{v}_j\notin E$ and $v_i,v_j\in V.$

$$\begin{array}{ccc}& & v\in \{v_2,v_4,\cdots ,v_n\},|N_s\left(v\right)\cap \{v_1,v_3,\cdots .v_{n-1}\}|=2>\hfill \\ & & 0=|N_s\left(v\right)\cap \{v_2,v_4,\cdots ,v_n\}|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \{v_1,v_3,\cdots ,v_{n-1}\},|N_s\left(v\right)\cap \{v_1,v_3,\cdots .v_{n-1}\}|>\hfill \\ & & |N_s\left(v\right)\cap (V\setminus \{v_1,v_3,\cdots .v_{n-1}\})|\hfill \end{array}$$

It implies $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\{v_1,v_3,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_1,v_3,\cdots ,v_{n-1}\},$ then

$$\begin{array}{ccc}& & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1=1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1\neg >1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $\{v_1,v_3,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_1,v_3,\cdots ,v_{n-1}\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 83. 

Let $NSHG:(V,E)$ be an odd neutrosophic SuperHyperCycle. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S=\{v_2,v_4,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\Gamma =\lfloor \frac{n}{2}\rfloor +1$ and corresponded neutrosophic SuperHyperSet is $S=\{v_2,v_4,\cdots ,v_{n-1}\}$;

$\left(iii\right)$

${\Gamma }_s=min\{{\Sigma }_{s\in S=\{v_2,v_4,\cdots .v_{n-1}\}}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right),{\Sigma }_{s\in S=\{v_1,v_3,\cdots .v_{n-1}\}}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\};$

$\left(iv\right)$

the neutrosophic SuperHyperSets $S_1=\{v_2,v_4,\cdots .v_{n-1}\}$ and $S_2=\{v_1,v_3,\cdots .v_{n-1}\}$ are only dual 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is an odd neutrosophic SuperHyperCycle. Let $S=\{v_2,v_4,\cdots ,v_{n-1}\}$ where for all $v_i,v_j\in \{v_2,v_4,\cdots ,v_{n-1}\},v_i{v}_j\notin E$ and $v_i,v_j\in V.$

$$\begin{array}{ccc}& & v\in \{v_1,v_3,\cdots ,v_n\},|N_s\left(v\right)\cap \{v_2,v_4,\cdots .v_{n-1}\}|=2>\hfill \\ & & 0=|N_s\left(v\right)\cap \{v_1,v_3,\cdots ,v_n\}|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \{v_2,v_4,\cdots ,v_{n-1}\},|N_s\left(v\right)\cap \{v_2,v_4,\cdots .v_{n-1}\}|>\hfill \\ & & |N_s\left(v\right)\cap (V\setminus \{v_2,v_4,\cdots .v_{n-1}\})|\hfill \end{array}$$

It implies $S=\{v_2,v_4,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\{v_2,v_4,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_2,v_4,\cdots ,v_{n-1}\},$ then

$$\begin{array}{ccc}& & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1=1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1\neg >1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $\{v_2,v_4,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_2,v_4,\cdots ,v_{n-1}\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_2,v_4,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right)$ and $\left(iii\right)$ are trivial.

$\left(iv\right).$ By $\left(i\right),$$S_1=\{v_2,v_4,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s enough to show that $S_2=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Suppose $NSHG:(V,E)$ is an odd neutrosophic SuperHyperCycle. Let $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ where for all $v_i,v_j\in \{v_1,v_3,\cdots ,v_{n-1}\},v_i{v}_j\notin E$ and $v_i,v_j\in V.$

$$\begin{array}{ccc}& & v\in \{v_2,v_4,\cdots ,v_n\},|N_s\left(v\right)\cap \{v_1,v_3,\cdots .v_{n-1}\}|=2>\hfill \\ & & 0=|N_s\left(v\right)\cap \{v_2,v_4,\cdots ,v_n\}|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \{v_1,v_3,\cdots ,v_{n-1}\},|N_s\left(v\right)\cap \{v_1,v_3,\cdots .v_{n-1}\}|>\hfill \\ & & |N_s\left(v\right)\cap (V\setminus \{v_1,v_3,\cdots .v_{n-1}\})|\hfill \end{array}$$

It implies $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\{v_1,v_3,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_1,v_3,\cdots ,v_{n-1}\},$ then

$$\begin{array}{ccc}& & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1=1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|=1\neg >1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v_{i+1}\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $\{v_1,v_3,\cdots ,v_{n-1}\}-\left\{v_i\right\}$ where $v_i\in \{v_1,v_3,\cdots ,v_{n-1}\}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_1,v_3,\cdots ,v_{n-1}\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 84. 

Let $NSHG:(V,E)$ be neutrosophic SuperHyperStar. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S=\left\{c\right\}$ is a dual maximal 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\Gamma =1;$

$\left(iii\right)$

${\Gamma }_s={\Sigma }_{i=1}^3{\sigma }_i\left(c\right);$

$\left(iv\right)$

the neutrosophic SuperHyperSets $S=\left\{c\right\}$ and $S\subset S^{\prime }$ are only dual 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperStar.

$$\begin{array}{ccc}& & \forall v\in V\setminus \left\{c\right\},|N_s\left(v\right)\cap \left\{c\right\}|=1>\hfill \\ & & 0=|N_s\left(v\right)\cap (V\setminus \left\{c\right\})|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=1>\hfill \\ & & 0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \left\{c\right\},|N_s\left(v\right)\cap \left\{c\right\}|>|N_s\left(v\right)\cap (V\setminus \left\{c\right\})|\hfill \end{array}$$

It implies $S=\left\{c\right\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S=\left\{c\right\}-\left\{c\right\}=\varnothing ,$ then

$$\begin{array}{ccc}& & \exists v\in V\setminus S,|N_s\left(z\right)\cap S|=0=0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v\in V\setminus S,|N_s\left(z\right)\cap S|=0\neg >0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $S=\left\{c\right\}-\left\{c\right\}=\varnothing$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\left\{c\right\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right)$ and $\left(iii\right)$ are trivial.

$\left(iv\right).$ By $\left(i\right),$$S=\left\{c\right\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Thus it’s enough to show that $S\subseteq S^{\prime }$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperStar. Let $S\subseteq S^{\prime }.$

$$\begin{array}{ccc}& & \forall v\in V\setminus \left\{c\right\},|N_s\left(v\right)\cap \left\{c\right\}|=1>\hfill \\ & & 0=|N_s\left(v\right)\cap (V\setminus \left\{c\right\})|\forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|=1>\hfill \\ & & 0=|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \\ & & \forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|>|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \end{array}$$

It implies $S^{\prime }\subseteq S$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 85. 

Let $NSHG:(V,E)$ be neutrosophic SuperHyperWheel. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S=\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}$ is a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\Gamma =|\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}|;$

$\left(iii\right)$

${\Gamma }_s={\Sigma }_{\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right);$

$\left(iv\right)$

the neutrosophic SuperHyperSet $\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}$ is only a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperWheel. Let $S=\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}.$ There are either

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=2>1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \end{array}$$

or

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=3>0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \end{array}$$

It implies $S=\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S^{\prime }=\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}-\left\{z\right\}$ where $z\in S=\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n},$ then There are either

$$\begin{array}{ccc}& & \forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|=1<2=|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \\ & & \forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|<|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \\ & & \forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|\neg >|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \end{array}$$

or

$$\begin{array}{ccc}& & \forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|=1=1=|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \\ & & \forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|=|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \\ & & \forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|\neg >|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \end{array}$$

So $S^{\prime }=\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}-\left\{z\right\}$ where $z\in S=\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S=\{v_1,v_3\}\cup {\{v_6,v_9\cdots ,v_{i+6},\cdots ,v_n\}}_{i=1}^{6+3(i-1)\le n}$ is a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right),$$\left(iii\right)$ and $\left(iv\right)$ are obvious. □

Proposition 86. 

Let $NSHG:(V,E)$ be an odd neutrosophic SuperHyperComplete. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\Gamma =\lfloor \frac{n}{2}\rfloor +1;$

$\left(iii\right)$

${\Gamma }_s=min{\left\{{\Sigma }_{s\in S}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\right\}}_{S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}};$

$\left(iv\right)$

the neutrosophic SuperHyperSet $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ is only a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is an odd neutrosophic SuperHyperComplete. Let $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}.$ Thus

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=\lfloor \frac{n}{2}\rfloor +1>\lfloor \frac{n}{2}\rfloor -1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \end{array}$$

It implies $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S^{\prime }={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}-\left\{z\right\}$ where $z\in S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1},$ then

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=\lfloor \frac{n}{2}\rfloor =\lfloor \frac{n}{2}\rfloor =|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|\hfill \end{array}$$

So $S^{\prime }={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}-\left\{z\right\}$ where $z\in S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right),$$\left(iii\right)$ and $\left(iv\right)$ are obvious. □

Proposition 87. 

Let $NSHG:(V,E)$ be an even neutrosophic SuperHyperComplete. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\Gamma =\lfloor \frac{n}{2}\rfloor ;$

$\left(iii\right)$

${\Gamma }_s=min{\left\{{\Sigma }_{s\in S}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\right\}}_{S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }};$

$\left(iv\right)$

the neutrosophic SuperHyperSet $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ is only a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is an even neutrosophic SuperHyperComplete. Let $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }.$ Thus

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=\lfloor \frac{n}{2}\rfloor >\lfloor \frac{n}{2}\rfloor -1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

It implies $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. If $S^{\prime }={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }-\left\{z\right\}$ where $z\in S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor },$ then

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=\lfloor \frac{n}{2}\rfloor -1<\lfloor \frac{n}{2}\rfloor +1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $S^{\prime }={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }-\left\{z\right\}$ where $z\in S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. It induces $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ is a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right),$$\left(iii\right)$ and $\left(iv\right)$ are obvious. □

Proposition 88. 

Let $\mathcal{NSHF}:(V,E)$ be a m-neutrosophic SuperHyperFamily of neutrosophic SuperHyperStars with common neutrosophic SuperHyperVertex neutrosophic SuperHyperSet. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S=\{c_1,c_2,\cdots ,c_m\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF};$

$\left(ii\right)$

$\Gamma =m$ for $\mathcal{NSHF}:(V,E);$

$\left(iii\right)$

${\Gamma }_s={\Sigma }_{i=1}^m{\Sigma }_{j=1}^3{\sigma }_j\left(c_i\right)$ for $\mathcal{NSHF}:(V,E);$

$\left(iv\right)$

the neutrosophic SuperHyperSets $S=\{c_1,c_2,\cdots ,c_m\}$ and $S\subset S^{\prime }$ are only dual 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperStar.

$$\begin{array}{ccc}& & \forall v\in V\setminus \left\{c\right\},|N_s\left(v\right)\cap \left\{c\right\}|=1>\hfill \\ & & 0=|N_s\left(v\right)\cap (V\setminus \left\{c\right\})|\forall z\in V\setminus S,|N_s\left(z\right)\cap S|=1>\hfill \\ & & 0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & v\in V\setminus \left\{c\right\},|N_s\left(v\right)\cap \left\{c\right\}|>|N_s\left(v\right)\cap (V\setminus \left\{c\right\})|\hfill \end{array}$$

It implies $S=\{c_1,c_2,\cdots ,c_m\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ If $S=\left\{c\right\}-\left\{c\right\}=\varnothing ,$ then

$$\begin{array}{ccc}& & \exists v\in V\setminus S,|N_s\left(z\right)\cap S|=0=0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v\in V\setminus S,|N_s\left(z\right)\cap S|=0\neg >0=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \exists v\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $S=\left\{c\right\}-\left\{c\right\}=\varnothing$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ It induces $S=\{c_1,c_2,\cdots ,c_m\}$ is a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$

$\left(ii\right)$ and $\left(iii\right)$ are trivial.

$\left(iv\right).$ By $\left(i\right),$$S=\{c_1,c_2,\cdots ,c_m\}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ Thus it’s enough to show that $S\subseteq S^{\prime }$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ Suppose $NSHG:(V,E)$ is a neutrosophic SuperHyperStar. Let $S\subseteq S^{\prime }.$

$$\begin{array}{ccc}& & \forall v\in V\setminus \left\{c\right\},|N_s\left(v\right)\cap \left\{c\right\}|=1>\hfill \\ & & 0=|N_s\left(v\right)\cap (V\setminus \left\{c\right\})|\forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|=1>\hfill \\ & & 0=|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \\ & & \forall z\in V\setminus S^{\prime },|N_s\left(z\right)\cap S^{\prime }|>|N_s\left(z\right)\cap (V\setminus S^{\prime })|\hfill \end{array}$$

It implies $S^{\prime }\subseteq S$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ □

Proposition 89. 

Let $\mathcal{NSHF}:(V,E)$ be an m-neutrosophic SuperHyperFamily of odd neutrosophic SuperHyperComplete neutrosophic SuperHyperGraphs with common neutrosophic SuperHyperVertex neutrosophic SuperHyperSet. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ is a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF};$

$\left(ii\right)$

$\Gamma =\lfloor \frac{n}{2}\rfloor +1$ for $\mathcal{NSHF}:(V,E);$

$\left(iii\right)$

${\Gamma }_s=min{\left\{{\Sigma }_{s\in S}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\right\}}_{S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}}$ for $\mathcal{NSHF}:(V,E);$

$\left(iv\right)$

the neutrosophic SuperHyperSets $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ are only a dual maximal 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is odd neutrosophic SuperHyperComplete. Let $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}.$ Thus

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=\lfloor \frac{n}{2}\rfloor +1>\lfloor \frac{n}{2}\rfloor -1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|\hfill \end{array}$$

It implies $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ If $S^{\prime }={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}-\left\{z\right\}$ where $z\in S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1},$ then

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=\lfloor \frac{n}{2}\rfloor =\lfloor \frac{n}{2}\rfloor =|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|\hfill \end{array}$$

So $S^{\prime }={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}-\left\{z\right\}$ where $z\in S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ It induces $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor +1}$ is a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$

$\left(ii\right),$$\left(iii\right)$ and $\left(iv\right)$ are obvious. □

Proposition 90. 

Let $\mathcal{NSHF}:(V,E)$ be a m-neutrosophic SuperHyperFamily of even neutrosophic SuperHyperComplete neutrosophic SuperHyperGraphs with common neutrosophic SuperHyperVertex neutrosophic SuperHyperSet. Then

$\left(i\right)$

the neutrosophic SuperHyperSet $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E);$

$\left(ii\right)$

$\Gamma =\lfloor \frac{n}{2}\rfloor$ for $\mathcal{NSHF}:(V,E);$

$\left(iii\right)$

${\Gamma }_s=min{\left\{{\Sigma }_{s\in S}{\Sigma }_{i=1}^3{\sigma }_i\left(s\right)\right\}}_{S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }}$ for $\mathcal{NSHF}:(V,E);$

$\left(iv\right)$

the neutrosophic SuperHyperSets $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ are only dual maximal 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is even neutrosophic SuperHyperComplete. Let $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }.$ Thus

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=\lfloor \frac{n}{2}\rfloor >\lfloor \frac{n}{2}\rfloor -1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|>|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

It implies $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ is a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ If $S^{\prime }={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }-\left\{z\right\}$ where $z\in S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor },$ then

$$\begin{array}{ccc}& & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|=\lfloor \frac{n}{2}\rfloor -1<\lfloor \frac{n}{2}\rfloor +1=|N_s\left(z\right)\cap (V\setminus S)|\hfill \\ & & \forall z\in V\setminus S,|N_s\left(z\right)\cap S|\neg >|N_s\left(z\right)\cap (V\setminus S)|.\hfill \end{array}$$

So $S^{\prime }={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }-\left\{z\right\}$ where $z\in S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ isn’t a dual neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$ It induces $S={\left\{v_i\right\}}_{i=1}^{\lfloor \frac{n}{2}\rfloor }$ is a dual maximal neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing for $\mathcal{NSHF}:(V,E).$

$\left(ii\right),$$\left(iii\right)$ and $\left(iv\right)$ are obvious. □

Proposition 91. 

Let $NSHG:(V,E)$ be a strong neutrosophic SuperHyperGraph. Then following statements hold;

$\left(i\right)$

if $s\ge t$ and a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices is an t-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, then S is an s-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

if $s\le t$ and a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices is a dual t-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, then S is a dual s-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Consider a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices is an t-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<t;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<t\le s;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<s.\hfill \end{array}$$

Thus S is an s-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Consider a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices is a dual t-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>t;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>t\ge s;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>s.\hfill \end{array}$$

Thus S is a dual s-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 92. 

Let $NSHG:(V,E)$ be a strong neutrosophic SuperHyperGraph. Then following statements hold;

$\left(i\right)$

if $s\ge t+2$ and a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices is an t-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, then S is an s-neutrosophic SuperHyperPowerful 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

if $s\le t$ and a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices is a dual t-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, then S is a dual s-neutrosophic SuperHyperPowerful 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Consider a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices is an t-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<t;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<t\le t+2\le s;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<s.\hfill \end{array}$$

Thus S is an $(t+2)-$neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. By S is an $s-$neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing and S is a dual $(s+2)-$neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, S is an s-neutrosophic SuperHyperPowerful 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a strong neutrosophic SuperHyperGraph. Consider a neutrosophic SuperHyperSet S of neutrosophic SuperHyperVertices is a dual t-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>t;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>t\ge s>s-2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>s-2.\hfill \end{array}$$

Thus S is an $(s-2)-$neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. By S is an $(s-2)-$neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing and S is a dual $s-$neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing, S is an $s-$neutrosophic SuperHyperPowerful 1-failed neutrosophic SuperHyperForcing. □

Proposition 93. 

Let $NSHG:(V,E)$ be a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph. Then following statements hold;

$\left(i\right)$

if $\forall a\in S,|N_s\left(a\right)\cap S|<\lfloor \frac{r}{2}\rfloor +1,$ then $NSHG:(V,E)$ is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

if $\forall a\in V\setminus S,|N_s\left(a\right)\cap S|>\lfloor \frac{r}{2}\rfloor +1,$ then $NSHG:(V,E)$ is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right)$

if $\forall a\in S,|N_s\left(a\right)\cap V\setminus S|=0,$ then $NSHG:(V,E)$ is an r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right)$

if $\forall a\in V\setminus S,|N_s\left(a\right)\cap V\setminus S|=0,$ then $NSHG:(V,E)$ is a dual r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\lfloor \frac{r}{2}\rfloor +1-(\lfloor \frac{r}{2}\rfloor -1);\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\lfloor \frac{r}{2}\rfloor +1-(\lfloor \frac{r}{2}\rfloor -1)<2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2.\hfill \end{array}$$

Thus S is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\lfloor \frac{r}{2}\rfloor +1-(\lfloor \frac{r}{2}\rfloor -1);\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\lfloor \frac{r}{2}\rfloor +1-(\lfloor \frac{r}{2}\rfloor -1)>2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2.\hfill \end{array}$$

Thus S is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<r-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<r-0=r;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<r.\hfill \end{array}$$

Thus S is an r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iv\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>r-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>r-0=r;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>r.\hfill \end{array}$$

Thus S is a dual r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 94. 

Let $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph. Then following statements hold;

$\left(i\right)$

$\forall a\in S,|N_s\left(a\right)\cap S|<\lfloor \frac{r}{2}\rfloor +1$ if $NSHG:(V,E)$ is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\forall a\in V\setminus S,|N_s\left(a\right)\cap S|>\lfloor \frac{r}{2}\rfloor +1$ if $NSHG:(V,E)$ is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right)$

$\forall a\in S,|N_s\left(a\right)\cap V\setminus S|=0$ if $NSHG:(V,E)$ is an r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right)$

$\forall a\in V\setminus S,|N_s\left(a\right)\cap V\setminus S|=0$ if $NSHG:(V,E)$ is a dual r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2=\lfloor \frac{r}{2}\rfloor +1-(\lfloor \frac{r}{2}\rfloor -1);\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\lfloor \frac{r}{2}\rfloor +1-(\lfloor \frac{r}{2}\rfloor -1);\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|=\lfloor \frac{r}{2}\rfloor +1,|N_s\left(t\right)\cap (V\setminus S)|=\lfloor \frac{r}{2}\rfloor -1.\hfill \end{array}$$

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2=\lfloor \frac{r}{2}\rfloor +1-(\lfloor \frac{r}{2}\rfloor -1);\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\lfloor \frac{r}{2}\rfloor +1-(\lfloor \frac{r}{2}\rfloor -1);\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|=\lfloor \frac{r}{2}\rfloor +1,|N_s\left(t\right)\cap (V\setminus S)=\lfloor \frac{r}{2}\rfloor -1.\hfill \end{array}$$

$\left(iii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and an r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<r;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<r=r-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<r-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|=r,|N_s\left(t\right)\cap (V\setminus S)|=0.\hfill \end{array}$$

$\left(iv\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and a dual r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>r;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>r=r-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>r-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|=r,|N_s\left(t\right)\cap (V\setminus S)|=0.\hfill \end{array}$$

□

Proposition 95. 

Let $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperComplete. Then following statements hold;

$\left(i\right)$

$\forall a\in S,|N_s\left(a\right)\cap S|<\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1$ if $NSHG:(V,E)$ is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\forall a\in V\setminus S,|N_s\left(a\right)\cap S|>\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1$ if $NSHG:(V,E)$ is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right)$

$\forall a\in S,|N_s\left(a\right)\cap V\setminus S|=0$ if $NSHG:(V,E)$ is an $(\mathcal{O}-1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right)$

$\forall a\in V\setminus S,|N_s\left(a\right)\cap V\setminus S|=0$ if $NSHG:(V,E)$ is a dual $(\mathcal{O}-1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and an 2- neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2=\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1-(\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1);\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1-(\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1);\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|=\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1,|N_s\left(t\right)\cap (V\setminus S)|=\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1.\hfill \end{array}$$

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2=\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1-(\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1);\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1-(\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1);\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|=\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1,|N_s\left(t\right)\cap (V\setminus S)=\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1.\hfill \end{array}$$

$\left(iii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and an ($\mathcal{O}-1$)-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\mathcal{O}-1;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\mathcal{O}-1=\mathcal{O}-1-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\mathcal{O}-1-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|=\mathcal{O}-1,|N_s\left(t\right)\cap (V\setminus S)|=0.\hfill \end{array}$$

$\left(iv\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and a dual r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\mathcal{O}-1;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\mathcal{O}-1=\mathcal{O}-1-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\mathcal{O}-1-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|=\mathcal{O}-1,|N_s\left(t\right)\cap (V\setminus S)|=0.\hfill \end{array}$$

□

Proposition 96. 

Let $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperComplete. Then following statements hold;

$\left(i\right)$

if $\forall a\in S,|N_s\left(a\right)\cap S|<\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1,$ then $NSHG:(V,E)$ is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

if $\forall a\in V\setminus S,|N_s\left(a\right)\cap S|>\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1,$ then $NSHG:(V,E)$ is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right)$

if $\forall a\in S,|N_s\left(a\right)\cap V\setminus S|=0,$ then $NSHG:(V,E)$ is $(\mathcal{O}-1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right)$

if $\forall a\in V\setminus S,|N_s\left(a\right)\cap V\setminus S|=0,$ then $NSHG:(V,E)$ is a dual $(\mathcal{O}-1)$-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperComplete. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1-(\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1);\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1-(\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1)<2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2.\hfill \end{array}$$

Thus S is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperComplete. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1-(\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1);\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\lfloor \frac{\mathcal{O}-1}{2}\rfloor +1-(\lfloor \frac{\mathcal{O}-1}{2}\rfloor -1)>2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2.\hfill \end{array}$$

Thus S is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperComplete. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\mathcal{O}-1-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\mathcal{O}-1-0=\mathcal{O}-1;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<\mathcal{O}-1.\hfill \end{array}$$

Thus S is an ($\mathcal{O}-1$)-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iv\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is a neutrosophic SuperHyperComplete. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\mathcal{O}-1-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\mathcal{O}-1-0=\mathcal{O}-1;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>\mathcal{O}-1.\hfill \end{array}$$

Thus S is a dual ($\mathcal{O}-1$)-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

Proposition 97. 

Let $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is neutrosophic SuperHyperCycle. Then following statements hold;

$\left(i\right)$

$\forall a\in S,|N_s\left(a\right)\cap S|<2$ if $NSHG:(V,E))$ is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

$\forall a\in V\setminus S,|N_s\left(a\right)\cap S|>2$ if $NSHG:(V,E)$ is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right)$

$\forall a\in S,|N_s\left(a\right)\cap V\setminus S|=0$ if $NSHG:(V,E)$ is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right)$

$\forall a\in V\setminus S,|N_s\left(a\right)\cap V\setminus S|=0$ if $NSHG:(V,E)$ is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and S is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2=2-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|<2,|N_s\left(t\right)\cap (V\setminus S)|=0.\hfill \end{array}$$

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and S is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2=2-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|>2,|N_s\left(t\right)\cap (V\setminus S)=0.\hfill \end{array}$$

$\left(iii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and S is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2=2-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|<2,|N_s\left(t\right)\cap (V\setminus S)|=0.\hfill \end{array}$$

$\left(iv\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph and S is a dual r-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2=2-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|>2,|N_s\left(t\right)\cap (V\setminus S)|=0.\hfill \end{array}$$

□

Proposition 98. 

Let $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is neutrosophic SuperHyperCycle. Then following statements hold;

$\left(i\right)$

if $\forall a\in S,|N_s\left(a\right)\cap S|<2,$ then $NSHG:(V,E)$ is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(ii\right)$

if $\forall a\in V\setminus S,|N_s\left(a\right)\cap S|>2,$ then $NSHG:(V,E)$ is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iii\right)$

if $\forall a\in S,|N_s\left(a\right)\cap V\setminus S|=0,$ then $NSHG:(V,E)$ is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing;

$\left(iv\right)$

if $\forall a\in V\setminus S,|N_s\left(a\right)\cap V\setminus S|=0,$ then $NSHG:(V,E)$ is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

Proof.$\left(i\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is neutrosophic SuperHyperCycle. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2-0=2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2.\hfill \end{array}$$

Thus S is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(ii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is neutrosophic SuperHyperCycle. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2-0=2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2.\hfill \end{array}$$

Thus S is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iii\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is neutrosophic SuperHyperCycle. Then

$$\begin{array}{ccc}& & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2-0;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2-0=2;\hfill \\ & & \forall t\in S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|<2.\hfill \end{array}$$

Thus S is an 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing.

$\left(iv\right).$ Suppose $NSHG:(V,E)$ is a[an] [r-]neutrosophic SuperHyperUniform-strong-neutrosophic SuperHyperGraph which is neutrosophic SuperHyperCycle. Then

$$\begin{array}{ccc}& & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2-0;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2-0=2;\hfill \\ & & \forall t\in V\setminus S,|N_s\left(t\right)\cap S|-|N_s\left(t\right)\cap (V\setminus S)|>2.\hfill \end{array}$$

Thus S is a dual 2-neutrosophic SuperHyperDefensive 1-failed neutrosophic SuperHyperForcing. □

5. Applications in Cancer’s Neutrosophic Recognition

The cancer is the disease but the model is going to figure out what’s going on this phenomenon. The special case of this disease is considered and as the consequences of the model, some parameters are used. The cells are under attack of this disease but the moves of the cancer in the special region are the matter of mind. The neutrosophic recognition of the cancer could help to find some treatments for this disease.

In the following, some steps are devised on this disease.

Step 

1. (Definition) The neutrosophic recognition of the cancer in the long-term function.

Step 

2. (Issue) The specific region has been assigned by the model [it’s called neutrosophic SuperHyperGraph] and the long cycle of the move from the cancer is identified by this research. Sometimes the move of the cancer hasn’t be easily identified since there are some determinacy, indeterminacy and neutrality about the moves and the effects of the cancer on that region; this event leads us to choose another model [it’s said to be neutrosophic SuperHyperGraph] to have convenient perception on what’s happened and what’s done.

Step 

3. (Model) There are some specific models, which are well-known and they’ve got the names, and some general models. The moves and the traces of the cancer on the complex tracks and between complicated groups of cells could be fantasized by a neutrosophic SuperHyperPath(-/neutrosophic SuperHyperCycle, neutrosophic SuperHyperStar, neutrosophic SuperHyperBipartite, neutrosophic SuperHyperMultipartite, neutrosophic SuperHyperWheel). The aim is to find either the 1-failed neutrosophic SuperHyperForcing or the neutrosophic 1-failed neutrosophic SuperHyperForcing in those neutrosophic SuperHyperModels.

5.1. Case 1: The Initial Steps Toward neutrosophic SuperHyperBipartite as neutrosophic SuperHyperModel

Step 

4. (Solution) In the Figure (27), the neutrosophic SuperHyperBipartite is highlighted and featured.

By using the Figure (27) and the Table (10), the neutrosophic SuperHyperBipartite is obtained.

Table 10. The Values of Vertices, SuperVertices, Edges, HyperEdges, and neutrosophic SuperHyperEdges Belong to The neutrosophic SuperHyperBipartite

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The neutrosophic SuperHyperEdges	The maximum Values of Its Endpoints

Table 10. The Values of Vertices, SuperVertices, Edges, HyperEdges, and neutrosophic SuperHyperEdges Belong to The neutrosophic SuperHyperBipartite

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The neutrosophic SuperHyperEdges	The maximum Values of Its Endpoints

5.2. Case 2: The Increasing Steps Toward Neutrosophic SuperHyperMultipartite as Neutrosophic SuperHyperModel

Step 

4. (Solution) In the Figure (28), the neutrosophic SuperHyperMultipartite is highlighted and featured.

Figure 28. A neutrosophic SuperHyperMultipartite Associated to the Notions of 1-failed neutrosophic SuperHyperForcing.

Figure 28. A neutrosophic SuperHyperMultipartite Associated to the Notions of 1-failed neutrosophic SuperHyperForcing.

By using the Figure (28) and the Table (11), the neutrosophic SuperHyperMultipartite is obtained.

Table 11. The Values of Vertices, SuperVertices, Edges, HyperEdges, and neutrosophic SuperHyperEdges Belong to The neutrosophic SuperHyperMultipartite

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The neutrosophic SuperHyperEdges	The maximum Values of Its Endpoints

Table 11. The Values of Vertices, SuperVertices, Edges, HyperEdges, and neutrosophic SuperHyperEdges Belong to The neutrosophic SuperHyperMultipartite

The Values of The Vertices	The Number of Position in Alphabet
The Values of The SuperVertices	The maximum Values of Its Vertices
The Values of The Edges	The maximum Values of Its Vertices
The Values of The HyperEdges	The maximum Values of Its Vertices
The Values of The neutrosophic SuperHyperEdges	The maximum Values of Its Endpoints