Intracellular “In Silico Microscopes” – Fully 3D Spatio-Temporal Virus Replication Model Simulations

1. Introduction

1.1. Biological basics

Virus endemics and pandemics belong to the present and next-future urging threats to worldwide health care management, economic prosperity, justice of basic goods distribution, democratic order, and human and animal existence at all [1,2,3,4,5,6].

To be prepared for the next pandemics better than for the recent COVID19 [7] one caused by the SarsCov2 virus, basic principles of virus replication need to be unveiled profound and with the complete possibilities modern natural science offers.

The well-known SarsCov2 virus belongs to the family of plus standed RNA / (+)ssRNA viruses[8], which show a comparably simple virus replication strategy, and therefore have the potential for first groundbreaking approaches to unveil virus replication.

In fact, the Hepatitis C virus (HCV) belongs as well to the family of plus stranded RNA / (+)ssRNA viruses and is the main reason for liver transplants in western countries [5,9].

Therefore, within decades of scientific research, HCV was investigated in detail by experimental virologists work [10,11,12]. Based on the knowledge gained in this course, it was possible to develop direct antiviral agents (DAA) which have the capacity to eliminate HCV completely, i.e., to clear the patients blood permanently from HCV [13,14,15].

So far, the DAAs developed for HCV are the only DAAs available in the field which allow to clear the virus load in patients completely. While this is a great success for science, it is due to a huge amount of experimental research which enabled in part substantial qualitative understanding of the virus dynamics. However, the success is due not completely to fully basic quantitative biophysical understanding, but also due to a mixture of the experiments combined with a lot of attempts. However, systematic development of DAAs is still in the beginning phase. More detailed quantitative understanding of viral replication mechanisms is urgently needed.

Also kinetic mathematical models [16,17,18,19,20,21,22,23,24] using ordinary differential equation (ODE) descriptions were developed for HCV infection to supply new findings, such as to figure out optimal doses of DAAs and other antiviral agents.

Some studies incorporate spatial effects of virus replication, cf. e.g. [25,26,27,28,29,30,31]. Still, the available extended experimental data bear potential for more detailed mathematical models and numerical simulations.

In particular, this holds true for complementary approaches combining highly spatially resolved experimental data of virus research with spatial model simulations at an intracellular level.

For example, in case of HCV, the virus genome replication factories are located inside of intracellular structures called membranous webs (MW). The MWs can be considered as regions which arise due to remodelling processes of the Endoplasmatic Reticulum (ER). More in detail but still very superficial, the MWs can be considered as accumulation zones of NSPs, which grow on top of the ER surface. The ER itself is an intracellular network with tubular interconnected structure, and the ER surface encloses the ER lumen.

Mathematically spoken, the ER surface is a connected sum of g tori, with $g\ge 1$. Thus, the ER surface is a 3D embedded curved 2D manifold. and is the exterior boundary of the ER lumen which is a connected 3D volume set.

Up to now, the very advanced experimental data such as highly spatially resolved fluorescence and electro-tomography data in many cases do not enter computational HCV viral RNA (vRNA) cycle models. This lack is due to the entire nature of kinetic ODE models: As kinetic ODE models by nature cannot account for the spatial structures, there is space for additional techniques. Partial differential equation (PDE) models allow for highly spatial and temporal resolved numerical simulations.

1.2. Former spatial models

Some years ago, we started to develop diffusion-reaction PDE models to enable fully 3D resolved “in silico microscope” like simulations [32,33,34]. The aim of these simulations was and is to mirror in vitro / in vivo experiments for the intracellular vRNA cycle dynamics.

The first models built upon two major HCV vRNA replication cycle properties: At first, the HCV NSPs attach to the ER surface directly after their cleavage from the polyprotein which is translated by the HCV vRNA. Once attached to the ER surface, the movement of the NSPs is exclusively restricted to the ER surface. Secondly, the vRNA movement properties and its spatial location have not been unveiled so far by experimental studies [35]. Further, we assumed that such a complex framework like spatial virus modeling in each case likely cannot start with quantitative exactness. Moreover, our first aim was to develop qualitative spatial models, and to adapt them step by step to quantitative experimental data.

Based on these basic starting point properties, we decided to develop at first models which described the principal components of the vRNA cycle: vRNA, NSPs, and a generic host factor. In particular, we decided to restrict the movement of all these components to the ER surface. Hence, the models we developed were realized as pure surface PDE (sufPDE) models. From the very beginning, we performed all model simulations upon experimental fluorescence data based z-stack data [36], and not on simplified structured meshes. The z-stack data were used as basis for realistic reconstructed ER geometries. The thus constructed 3D embedded 2D ER manifolds were realized as triangulized 2D dimensional unstructured grids embedded in the full 3D volume. The sufPDE components were defined such that they moved exactly upon these low dimensional embedded ER surface grids.

While it is unlikely that the host factor movement is restricted to the ER surface, even such comparably simple models allowed for interesting insights into the relation of form and function [32]. One interesting finding was about the relation of form and function: Sensitivity studies revealed that the movement “velocity”, i.e., the diffusion coefficient, of the host factor is more important for rapid vRNA genesis than the complete amount of host factor available in the cell, which could not be analyzed with standard ODE models.

As the first model did not distinguish between different modes of action of the three components (vRNA, NSP, host) and implemented a simplified multilinear reaction strategy, we extended the basic model structure [33]: Different aggregate states for different modes of action and Michael-Mentens kinetics / population dynamics inspired reaction and diffusion coefficients.

The movement of all components was still restricted to the ER surface, but the extended qualitative model already provoked several experimental validation options, and it allowed for model properties which were not realized by earlier mathematical virus models. For example, the so-called “cis-requirement” of HCV vRNA replication is the assumption that NSPs only replicate their originate HCV RNA. It was postulated based on experimental data [37,38] but arose also in a natural manner within the refined model [33].

In parallel to the development of qualitative models, we stated to estimate parameters relevant for spatial virus models [34,39,40]. In particular, we established a first estimate of the diffusion coefficient of the HCV NS5a protein. NS5a is a major HCV NSP and involved in nearly all steps of HCV replication [13,13,14] and inhibiting NS5a breaks the vRNA cycle [14]. We combined sufPDE computations of the NS5a movement restricted to the ER surface and adapted the simulation data to experimental FRAP (fluorescence recovery after photobleaching) data using the Gauss-Newton procedure, which allowed the first published estimation of the diffusion coefficient of a virus protein to the best of our knowledge [34].

The aim of spatial data estimations was to incorporate such values as parameters into the aforementioned so far qualitative models, to approach the simulation data to quantitative experimental values.

1.3. Aims of this study

The aim of this study is to merge effects restricted to the ER surface such as NSP diffusion with others taking place in the cytosol of the cell as the host factor supply. On this turn, we introduce realistic parameters for diffusion and reaction. For the reaction coefficients, we can get some inspiration from the ODE kinetic model literature. For the diffusion coefficients, we take inspiration from the aforementioned NS5a diffusion constant estimation procedure we performed before. In addition, we use quantitative parameters supported experimentally to approach to quantitative reliable simulations.

Concerning the technical framework of this study with biophysical background, we refer in part to a proceedings paper which we published recently [41]. As before, the simulations are performed upon realistic reconstructed cell geometries.

The model and the simulations presented in this study mimick the full HCV vRNA cycle evaluated at a cutout part of a hepatoma cell based upon the aforementioned z-stack data, where the ER surface and the MW zones were stained with calnexin as marker for the ER surface, and a dsRNA marker for the MW zones.

In particular, the model simulations now allow the vRNA and the host factor to move not only at the ER surface. The vRNA can move in the full cytosol volume, but also can attach to the ER surface and move exclusively there. The generic host factor movement takes place in the full cytosol volume. This accounts for the assumption that the cell energy which is delivered for virus replication should not be restricted to the ER surface. Finally, while the NSP movement itself is restricted to the ER surface, as indicated by experiment, the accumulation of the MW zones now takes place in the full volume of the MW regions. The domains where the MW regions are allowed to grow is given by the experimental z-stacks, where the volumes of the MW zones are separated from the rest of the cell.

These model properties allow for fully realistic vRNA cycle simulations.

The forthcoming chapters of this article will discuss in detail the consequences of our in silico approach and evaluate putative future in silico - in vitro combination research.

This paper is organized as follows:

In Section 2 “Materials, Models and Methods” we describe the new mathematical model of the vRNA cycle and the geometric base of our simulations. We also give insight into the solution techniques using modern supercomputers which allow to solve the computational model. In Section 3 “results”, we present the simulations of the new model and describe the computational results in the biological context. In Section 4 “discussion” we discuss the consequences of our new model approach in the context of modern experiments and analyze the quantitative reliability of our simulations in comparison with experimental data knowledge. The conclusion Section 5 summarize the major aspects of our study, and give an outlook to middle and long term prespectives of our framework in the context of virus research and combined in silico - in vitro research.

2. Materials, Models and Methods

We present a mathematical model of the HCV vRNA virus replication cycle and evaluate it on a cutout part of a realistic reconstructed hepatoma cell geometry.

This section starts describing the establishment of the unstructured grid which is based on experimental fluorescence data.

Afterwards we develop a complex nonlinear mathematical model of the vRNA cycle which couples surface and volume effects of the major components of the vRNA cycle.

Finally, this section describes the numerical solution techniques to perform the in silico simulations in a very efficient way on present supercomputers.

Here, we give a more superficial overview over the details concerning the mathematical and numerical properties. For a more detailed description of these properties, we refer to a peer reviewed proceedings paper which we published recently [41].

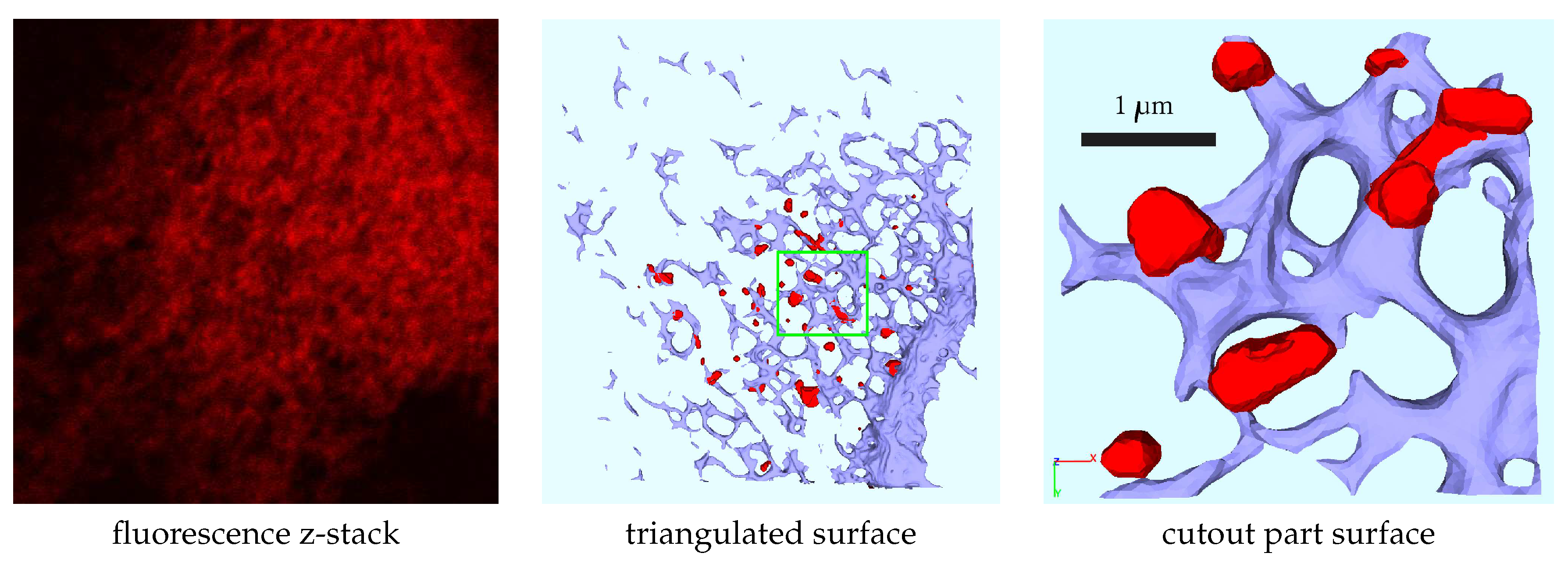
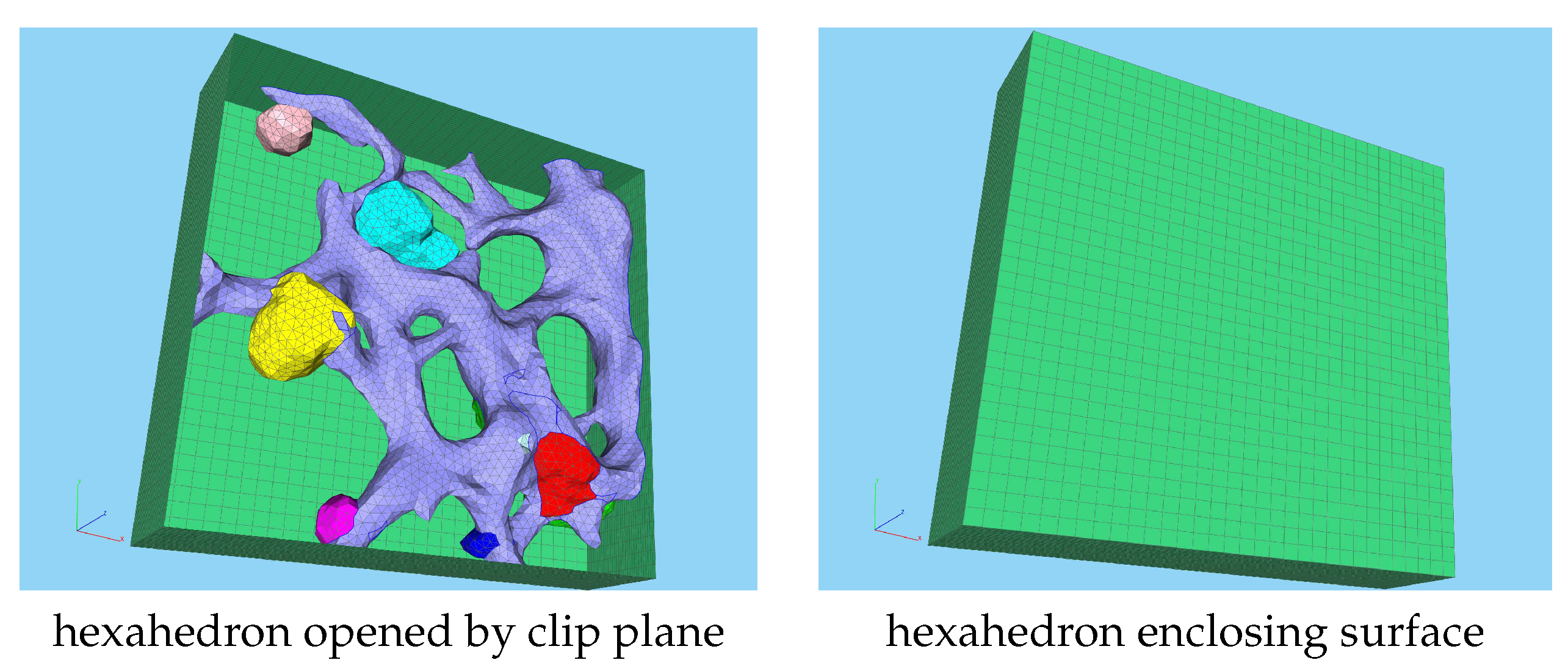
2.1. Experimental data based unstructured grid geometry

In brief:

The cell region where the simulations take place is based on the same data as in our former papers in this context [32,33]. However, we only considered the reconstructed surfaces of ER and MW previously. Here, we enclose the pure surface grid into a hexahedron and tetrahedralize the volume. We repeat the steps of the surface reconstruction based on fluorescence z-stack data and describe the volume mesh generation in detail.

Extended:

The experimental data basis of our geometries are stained fluorescence z-stack data of hepatoma cells [36]. The cells were labeled for two channels. Calnexin was used as marker for the ER surface and delivers the signature for the ER compartment boundary. To account for the MW regions, dsRNA marker was applied.

In our previous studies in this context, we used these experimental data based z-stack data for the reconstruction of the ER surface of the hepatoma cell and of the surface of the MWs of this cell [32,33]. The technical procedure delivered us triangular surface grids for the ER surface and the surfaces of the MW. These surfaces were merged into one computational surface grid, which served as computational domain of the sufPDE models which we simulated [32,33].

We recall in brief the surface reconstruction procedure: Based on a deblurring procedure of the original z-stack data performed by means of Huygens SVI [42,43,44,45], we used an anisotropic inertia-momentum based filter to shape the data [46]. The segmentation was performed with Otsu and Hysteresis techniques. Finally, the marching cubes algorithm established the triangular surface grids, separately for each of both channels (calnexin - ER / dsRNA - MW). For the complete reconstruction procedure, we used the GPGPU / CUDA based program NeuRA2 [46]. To perform the post processing of both surface grids and the merging of these two surface grids (ER/MW), we applied the program ProMesh4 [47,48,49].

The thus generated unstructured triangular surface grid described the relevant compartments of a complete hepatoma cell.

To enable fast and efficient investigations of the models, a subset of the complete surface grid was enclosed by a rectangular hexahedron as basis for the simulations [32,33]. In the visual 2D front view, the rectangular hexahedron covered roughly about 10 % of the complete region. The cell we used as basis for the simulation of the model was small compared to other cells we reconstructed [34,39]. Therefore, the total size of the computational domain was about 1-10 % of a typical hepatoma cell.

Figure 1 recalls the reconstruction, surface generation, and cutout process.

The thus generated surface grid served as basis for the simulations of our previously published model papers [32,50]. This surface grid hence represented a cutout part of the complete hepatoma cell, respectively the ER and the MWs inside the cutout region.

We recall also that we interpreted the intersections of ER surface and MW surfaces to be ribosomal regions.

For the simulations of this paper, the grid geometry generation was substantially extended [41]:

We enclosed the cutout part of the aforementioned ER / MW surface grid with (another, slightly bigger) rectangular hexahedron and tetrahedralized the interior volume region with the aid of Tetgen [51].

The ER lumen, i.e. the volume enclosed by the ER surface, was afterwards again exempt from the volume mesh.

In this way, we constructed a tetrahedralized 3D volume mesh, where the ER surface is an external boundary of the volume mesh, as well as the enclosing hexahedron.

The ribosomes are still interpreted to be the intersection of ER and MW surfaces. However, now, the MWs are constructed as volume regions, filling the interior part of the MW surfaces.

The other parts of the tetrahedralized volume is considered as cytosol.

Table 1 defines the name, the technical symbol, and the biological interpretation of the different subdomains of the volume grid.

Figure 2 displays the enclosing of (the cutout part of) the surface grid with a rectangular hexahedron to enable volume grid generation by means of tetrahedralization.

Figure 3 displays the subdomains of the surface grid and the volume mesh, i.e., the subdomains of the 3D computational domain $\Omega =\Gamma \cup C\cup W$. Note that $\Gamma$ is the external boundary of $\Omega \subset {\mathbb{R}}^3$.

We recall that $\mathcal{M}$ is embedded inside $\mathcal{C}\cup \mathcal{W}$ but the ER lumen described by the volume enclosed by $\mathcal{M}$ is excluded from the computational domain and not meshed. Therefore, $\Omega$ is not stellated, but $\mathcal{M}$ is entirely part of the “external” boundary of $\Omega$, i.e., $\Gamma =\mathcal{M}\cup \mathcal{B}$.

The thus generated mesh serves as computational domain of our simulations and represents the grid refinement level 0 in the context of global grid refinement strategies.

2.2. Laplace Beltrami and tangential space / manifold operators

As usual in differential geometry, we apply tangential operators for the mathematical operations at the manifold [52]. In particular, we label these operators with the index “T” to indicate that they project the operation under consideration to the tangential space of the embedded manifold.

We use explicitly nabla and gradient in the tangential space, ${\nabla }_{\mathrm{T}},di{v}_T$.

The Laplace operator transforms to the Laplace-Beltrami operator ${\Delta }_{\mathrm{T}}$.

2.3. Mathematical PDE model coupling surface and volume effects

The model we develop in this study follows the structure of that we introduced in [41] where we did not publish biophysical relevant results but focused on the numerical solution. Nevertheless, compared to the published coupled surface-volume model in [41], the model is again slightly improved. This does not refer to the structure itself but to some of the specific coefficients of diffusion and reaction which we improved to get closer to the supposed experimental reality.

Modelling the compartments of concentrations of the major components of the vRNA replication cycle, we take account for their spatial location as well for their mode of action. We define compartments living purely on the manifold and others living purely in the volume. A list of all concentrations is delivered in Table 2.

The mathematical diffusion-reaction model is based on the coupling of surPDEs, PDEs, and connecting boundary flux conditions of the PDEs which are reflected by reaction terms of the sufPDEs. The highly nonlinear structure of diffusion and reaction coefficients follows the principles introduced in [33] and reflects the central properties explained there. The coefficient structure is inspired by Michaelis-Menten kinetics to allow for relatively sharp increase of values and for plateaus, but is not a Michaelis-Menten model itself.

Defining ${\chi }_{{\mathcal{R}}_i}$ as the characteristic function of ${\mathcal{R}}_i$, i.e.,

$${\chi }_{{\mathcal{R}}_i}\left(\mathbf{x}\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathbf{x}\in {\mathcal{R}}_i,\hfill \\ 0,\hfill & \mathrm{if}\mathbf{x}\notin {\mathcal{R}}_i,\hfill \end{array}\right.$$

(1)

we use the following abbreviation terms:

$$\begin{array}{ccc}\hfill {\eta }_0\left(\mathbf{x}\right)& =& \frac{1}{{\displaystyle \sum _{i=1}^7}\left|{\mathcal{R}}_i\right|{\chi }_i\left(\mathbf{x}\right)+\delta }\left[{\displaystyle \sum _{j=1}^7}{\chi }_j\left(\mathbf{x}\right)\right]\hfill \end{array}$$

(2)

where $|{\mathcal{R}}_i|$ is the surface of ribosomal region ${\mathcal{R}}_i$, $i=1,2,\dots ,7$, and $\delta$ is a constant damp value given in $\mu m^2$ to be chosen. The values used in this study are shown in Table 3.

The notation of all equations does not indicate the spatial and temporal reference point for all compartments as this is the same in all compartments. In the forthcoming, we also write ${\eta }_0$ without explicitely referring to the spatial point x.

To develop the PDE system, we will further use several parameters which are listed in Table 3 together with their numerical values and units. The parameters with units are $r_i\in {\mathbb{R}}^{+}$, $i=1,2,\dots ,6$, which describe reaction processes and have unit $1/s$ (we assume $r_5<r_3$), the diffusion coefficients $D_R,D_P,D_N,D_R^S,D_C,D_R^V,D_H\in {\mathbb{R}}^{+}$ given in the unit $\frac{\mu m^2}{s}$ and the initial value of the host factor compartment $h_0$ with unit $\frac{1}{\mu m^3}$. The remaining parameters are dimensionless numbers: Coefficients $p_i\in {\mathbb{R}}^{+}$, $i=1,\dots ,10$, the coefficients $k_i\in {\mathbb{R}}^{+}$ for $i=1,\dots ,3$ and $v_1,v_2\in {\mathbb{N}}^{+}$ as well as $b\in {\mathbb{R}}^{+}$.

Further we use $\nu \in \mathbb{N}$.

With these definitions, we can establish the coupled sufPDE/PDE system:

The surPDEs read

(3)

$$\begin{array}{ccc}\hfill {\partial }_t{P}_R^S& =& {\left[di{v}_T\left(D_P{\nabla }_T{P}_R^S\right)+r_2{R}_R^S\frac{H^V}{H^V+p_3}848-r_3{P}_R^S\right]}_{\mathcal{R}}\hfill \end{array}$$

(4)

(5)

(6)

(7)

The “volume” PDEs (PDE/volPDE) read

(8)

(9)

(10)

(11)

$$\begin{array}{ccc}\hfill {\partial }_t{H}^V& =& ÷\left[D_H\left(1+k_3\frac{W_W^V}{W_W^V+p_9}\right)\nabla H^V\right]-{\left[v_2{r}_6{C}_W^V\frac{H^V}{H^V+p_8}\frac{W_W^V}{W_W^V+p_{10}}\right]}_{\mathcal{W}}\hfill \end{array}$$

(12)

The boundary conditions of the volPDEs connect reaction terms of the sufPDEs with the external boundary fluxes of the volume components to ensure strict mass conservation in the context of the interchange of components between manifold and volume:

(13)

We use colors to indicate the relation between the flux conditions of the boundaries of the volume and the reactions on the surface which ensure the conservation of mass in the exchange between manifold and volume. Overall the boundary flux conditions of the PDEs are mirrored by reactions of the sufPDE system. The reaction terms of the sufPDE system and their corresponding boundary condition terms of the PDE system are colored with the same color.

The initial conditions read:

$$\begin{array}{ccc}\hfill R_R^S(\overrightarrow{x},t=0)& =& \left\{\begin{array}{cc}{\eta }_0\left(\overrightarrow{x}\right)\hfill & \forall \overrightarrow{x}\in {\mathcal{R}}_2\hfill \\ 0\hfill & \forall \overrightarrow{x}\in \mathcal{M}\setminus {\mathcal{R}}_2\hfill \end{array}\right.\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill P_R^S(\overrightarrow{x},t=0)& =& 0\forall \overrightarrow{x}\in \mathcal{M}\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill W_C^S(\overrightarrow{x},t=0)& =& 0\forall \overrightarrow{x}\in \mathcal{M}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill N_E^S(\overrightarrow{x},t=0)& =& 0\forall \overrightarrow{x}\in \mathcal{M}\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill R_E^S(\overrightarrow{x},t=0)& =& 0\forall \overrightarrow{x}\in \mathcal{M}\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill W_W^V(\overrightarrow{x},t=0)& =& 0\forall \overrightarrow{x}\in \Omega \hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill N_W^V(\overrightarrow{x},t=0)& =& 0\forall \overrightarrow{x}\in \Omega \hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill C_W^V(\overrightarrow{x},t=0)& =& 0\forall \overrightarrow{x}\in \Omega \hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill R_P^V(\overrightarrow{x},t=0)& =& 0\forall \overrightarrow{x}\in \Omega \hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill H^V(\overrightarrow{x},t=0)& =& h_0\forall \overrightarrow{x}\in \Omega \hfill \end{array}$$

(23)

These conditions ensure that at one selected ribosomal region (we choose ${\mathcal{R}}_2$) the integral of the concentration of ribosomal bound vRNA in this ribosomal region starts with one. Biophysically, this can be interpreted that we have one bound vRNA at one ribosomal region at the beginning while all other concentrations except for the host factor start from zero. The host factor itself starts with an allover constant concentration $h_0$. In other words, in the beginning one vRNA is in the cell and the host factor is homogeneneosly distributed allover the cell. All other components which arise in the vRNA cycle are not present at time zero but will be produced upon the viral polyprotein translation, cleavage, NSP movement and MW accumulation, followed by vRNA polymerization and movement inducing the closure and repetition of the cycle at other ribosomal regions.

This model takes into account all major steps of the vRNA replication cycle. Details will also be demonstrated in the results section, Section 3.

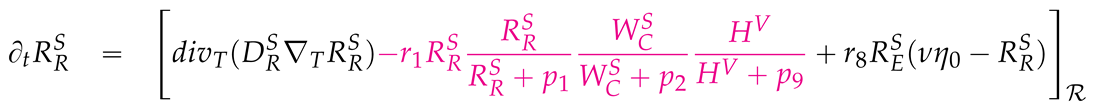
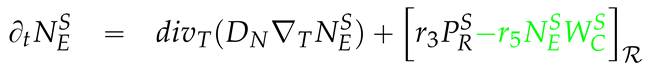
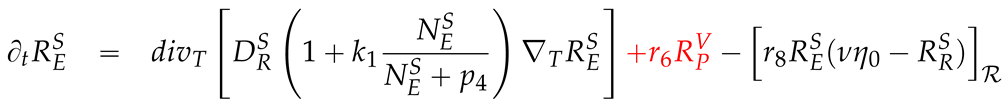
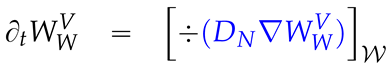
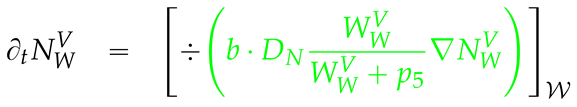
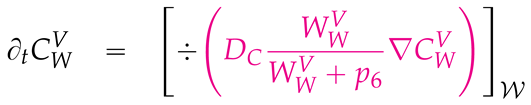
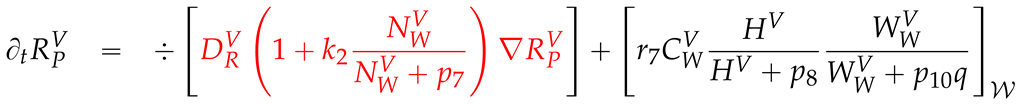
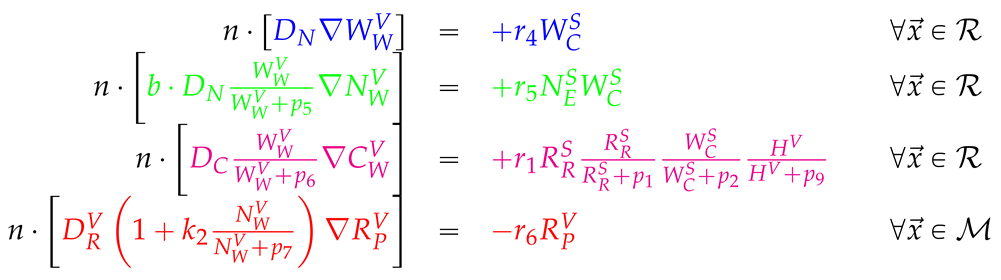
2.4. Numerical values of the model parameters

For the simulation in this study, we use the parameter values shown in Table 3. We also give some references but this does not necessarily refer to exact values but as basis for the size of magnitude of these parameters.

However, we emphasize that our model is not restricted to this parameter set, and parameter values may be further improved for more realistic description. There is need for further studies to calibrate the parameters and potentially also refine the model structure itself.

2.5. Numerical solution techniques to solve the sufPDE/PDE system

An extended description of the numerical solution techniques is given in [41]. Here, we repeat in brief the major issues.

The discretization in time is performed by means of an adaptive implicit Euler scheme of first order.

The discretization in space is established with the aid of a vertex-centered finite volume (vcFV) scheme, which is also called also “box method” [53,54]. This scheme guarantees the mass conservation of the transported components on the discrete level.

The sufPDE/PDE system (3)-(12) is solved with a nonlinear Newton solver. Each iteration of the Newton solver induces the establishment of a huge system of linear equations (SLE), which has sparse matrix structure. The SLEs are solved using a Geometric Multigrid Solver (GMG) preconditioned BiCGStab solver. The GMG applies a hierarchic grid distribution technique and hence allows highly efficient massively parallel solution of the system [55]. For more details of the hierarchic grid distribution based GMG solver and the numerical grid convergence challenges and solutions of the highly nonlinear model at the long term scale, we refer to [56]. As smoother, we use Symmetric Gauss-Seidel (SGS), and the base solver is a BiCGStab preconditioned with an ILU.

Table 4 displays the degrees of freedom (DoFs) at different grid levels.

The computations were performed at the HLRS Stuttgart Apollo Hawk Supercomputer. The final quantitative data evaluations shown in the results section below were achieved by grid refinement level 4 computations while the simulation movie (supplemental movie) and its screenshots are shown at grid refinement level 1 to save storage space.

2.6. Integrals of concentrations over subdomains

When simulating the model, also integrals of concentrations within specific subdomains are evaluated.

For integrals of a generic 3D embedded 2D manifold concentration $Q^S$ at the namifold over a generic subdomain $\mathcal{S}\subset \mathcal{M}$, we compute

$${\mathcal{I}}_{\mathcal{S}}\left(Q^S\right):={\int }_{\mathcal{S}}{Q}^S\mathrm{d}\sigma .$$

(24)

In case of a generic 3D volume concentration $Q^V$ within the volume over a generic subdomain $\mathcal{V}\subset \Omega$, we compute

$${\mathcal{I}}_{\mathcal{V}}\left(Q^V\right):={\int }_{\mathcal{V}}{Q}^V{\mathrm{d}}^{3}x.$$

(25)

Note that as surface concentrations are given per $\mu m^2$ while volume concentrations given per $\mu m^3$, the integrated values are all dimensionless numbers of components.

Therefore, exchange between volume and manifold is possible without restrictions because of the boundary conditions (13) which are mirrored by the reaction coefficients of the sufPDEs (3)-(7).

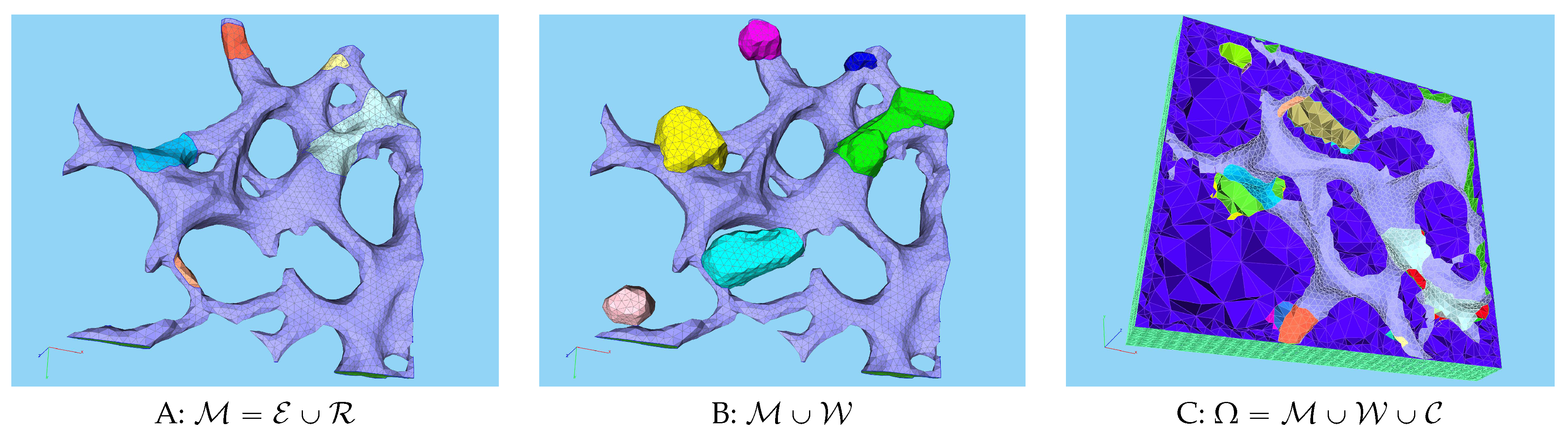
2.7. Distinguing between geometrically defined and biophysically active MW zones

Note that geometric regions as subdomains of the computational mesh, cf. Table 1 should be distinguished from the static and dynamic biophysical effects described by the model. This holds especially true in case of the MW.

The geometric MW zones play the role of potentially active MW zone but already exist from the beginning and are volume subdomains of our computational domain. They are defined by the dsRNA stained zones of the experimental z-stack data which are the geometric basis of our simulations. However, at the beginning of the simulations, biophysically, these zones have the same properties as the rest of the cytosol as the cell is considered to start in a healthy state.

We consider a geometric MW zone to be biophysically active MW zone only in case when a nonzero spatial concentration of viral WP exists inside this geometric MW zone. This happens when ribosomal bound WP detaches from the ribosomal zone of the ER which is flanking a geometric MW zone. In our model, WP which detaches from the ER surface is only allowed to diffuse into the geometric MW zone defined by the experimental z-stack data. Then, WP enters the MW zone and diffuses into the geometric MW volume and the respective MW zone becomes biophysically “active”.

Moreover, NS5a and the RC can detach from the surface only in case when a MW is already active, i.e. when there exists a nonzero WP concentration inside such a MW.

3. Results

We simulated the mathematical model that was introduced in the Materials, Models and Methods Section 2. Here, we illustrate the spatial data results of the simulations. We also give quantitative evaluations of integrals of the compartments to allow comparisons with published in vitro data and ODE kinetic model values which are averaged over the complete cell. We are not aware of published spatially resolved quantitative data itself and do not have access to such data.

Note that we describe our 3D simulation results as concentrations per unit volume element and per unit surface element, respectively. We refer to more conceptional details and extended explanations in Section “4.2.1. Interpretation of local concentrations” of [33]. We recall that we consider spatially resolved concentrations in our simulations rather then single particle models such as agent based random walk models.

3.1. Geometric basis and geometric vs. biophysical subdomains

The simulations are performed at realistic reconstructed grid geometries which are based on experimental fluorescence z-stack data. This data allows us to reconstruct the ER surface and the potential MW volume regions. The cytosol volume is surrounding the ER and the MW regions. The ER lumen is exempt from the vRNA cycle model. We consider the cut set of the ER surface and the boundaries (surfaces) of the MWs as ribosomal regions.

Note again that a potential geometric MW subdomain starts with having the same biophysical properties as the geometric cytosol subdomain as we start with a healthy state of the cell.

Our model does not allow NSPs/WPs to exist in or move into the entire cytosol subdomain. Hence, the cytosol subdomain always is biophysical cytosol.

WP, once cleaved from the viral polyprotein, at first is attached to the ER surface. However, the WPs can detach from the ER surface and diffuse (exclusively) into the volume of the geometric MW subdomain. Then the WP concentration is nonzero in the geometric MW subdomain and this geometric subdomain becomes a biophysically active MW zone with the respective biophysical properties.

For more details, we refer to Section 2.7.

3.2. Spatial simulation data evaluation – simulation movie

We now visualize the temporal evaluation of the 3D spatial simulation data at selected time points using a front view to the simulation data of the different compartments (recall Table 2).

3.2.1. Concentrations and their spatial regions

In the fully spatio-temporal resolved simulations, the following spatial compartments play a major role: the ER surface, the MW volumes, and the cytosol volume.

In the following screenshots, we will display all compartments described in Table 2: ribosomal bound vRNA, viral polyprotein, “web protein” (WP) as cleaved generic NSP except for NS5a, NS5a NSP, free vRNA, replication complex (RC), and a generic host factor. This host factor might be some sort of energy giving component of the cell, but is not specified here.

Some compartments are defined only either on the ER surface or in the volume of cytosol and/or only on the geometric potential MW subdomains, while others exist in both, surface and volume, modes. In the latter case, exchange between ER surface and volume is possible under certain conditions as specified by the model.

In detail, ribosomal bound vRNA and viral polyprotein exist only on the ribosomal zones of the ER surface. Free vRNA is attached/bound to the ER surface in one mode and moving in the complete volume in another mode. WP is restricted to the ribosomal zone of the ER surface in one mode and can further exist in the MW volumes as another mode. Similarly, NS5a moves over the complete ER surface in one mode but can also exist in the MW zones in another mode. The RC exists only in the MW volume zones and the host factor exists in the complete volume of cytosol and MW subdomains.

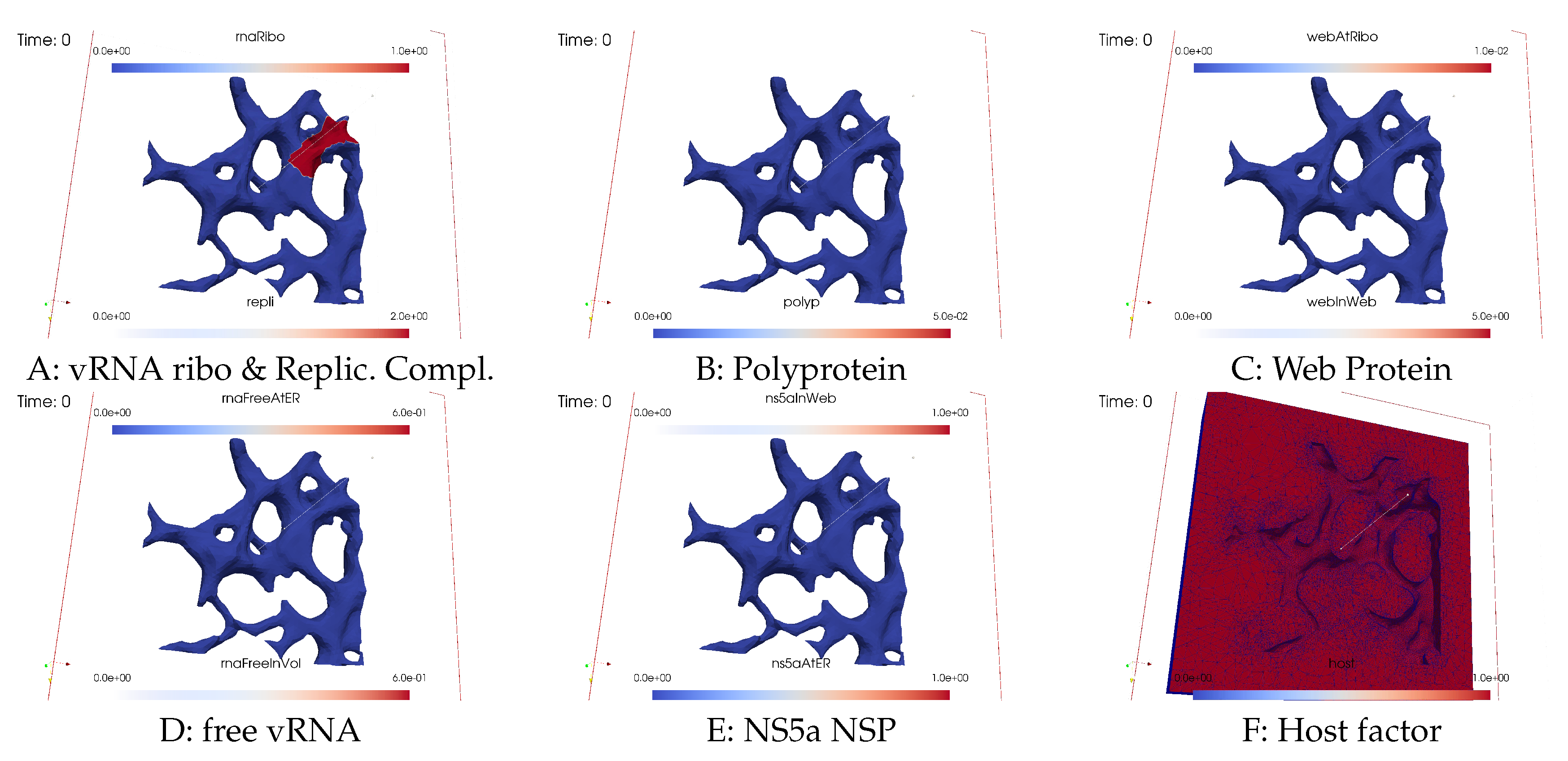
3.2.2. In silico microscope of vRNA cycle

We consider the simulation data as if we would look into some sort of “in silico” microscope. To facilitate the comparison of the different screenshots at different time points, we use the same scale for each respective component at all time points.

The total simulated biophysical time is about 7.5 hours.

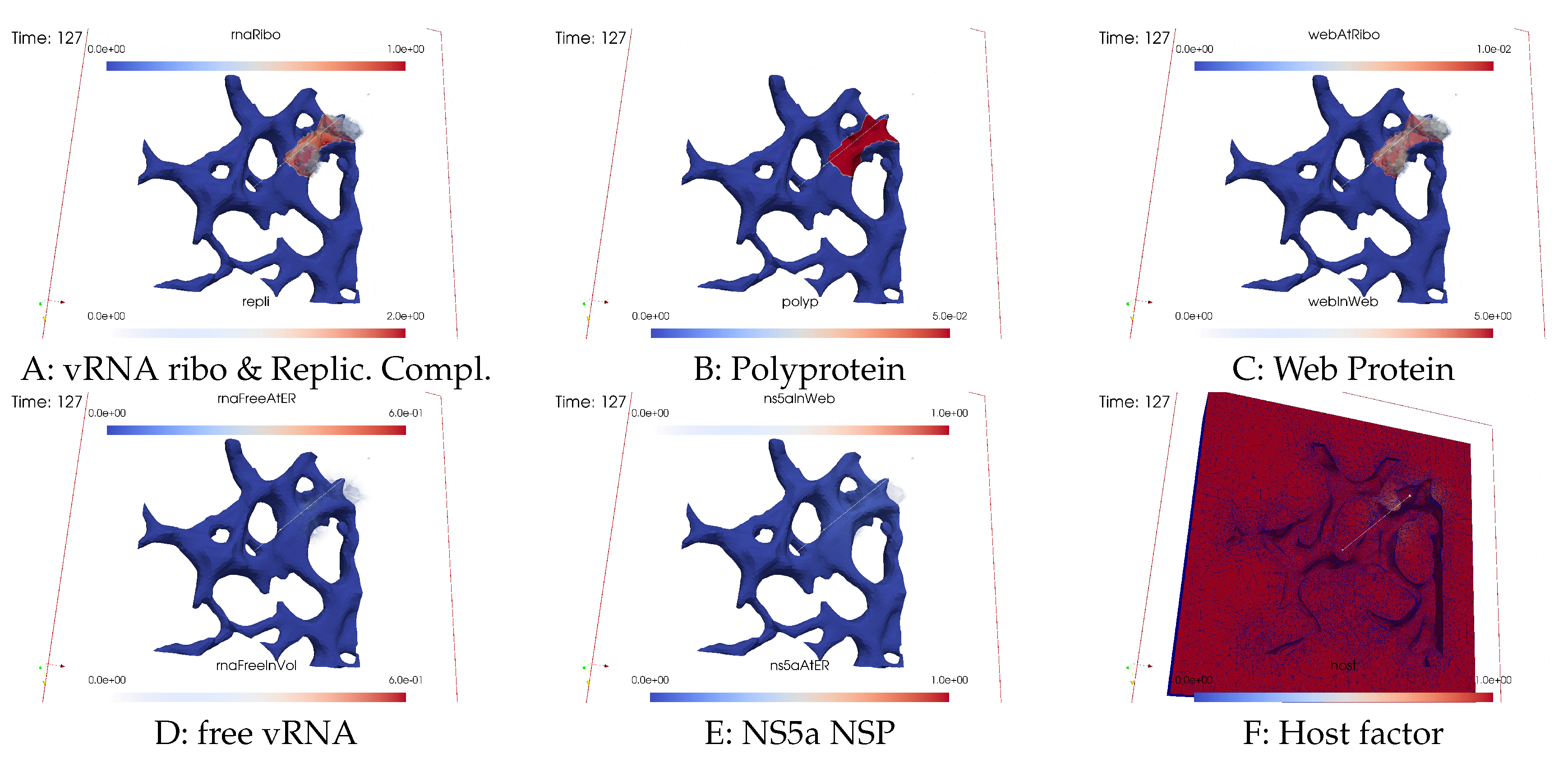
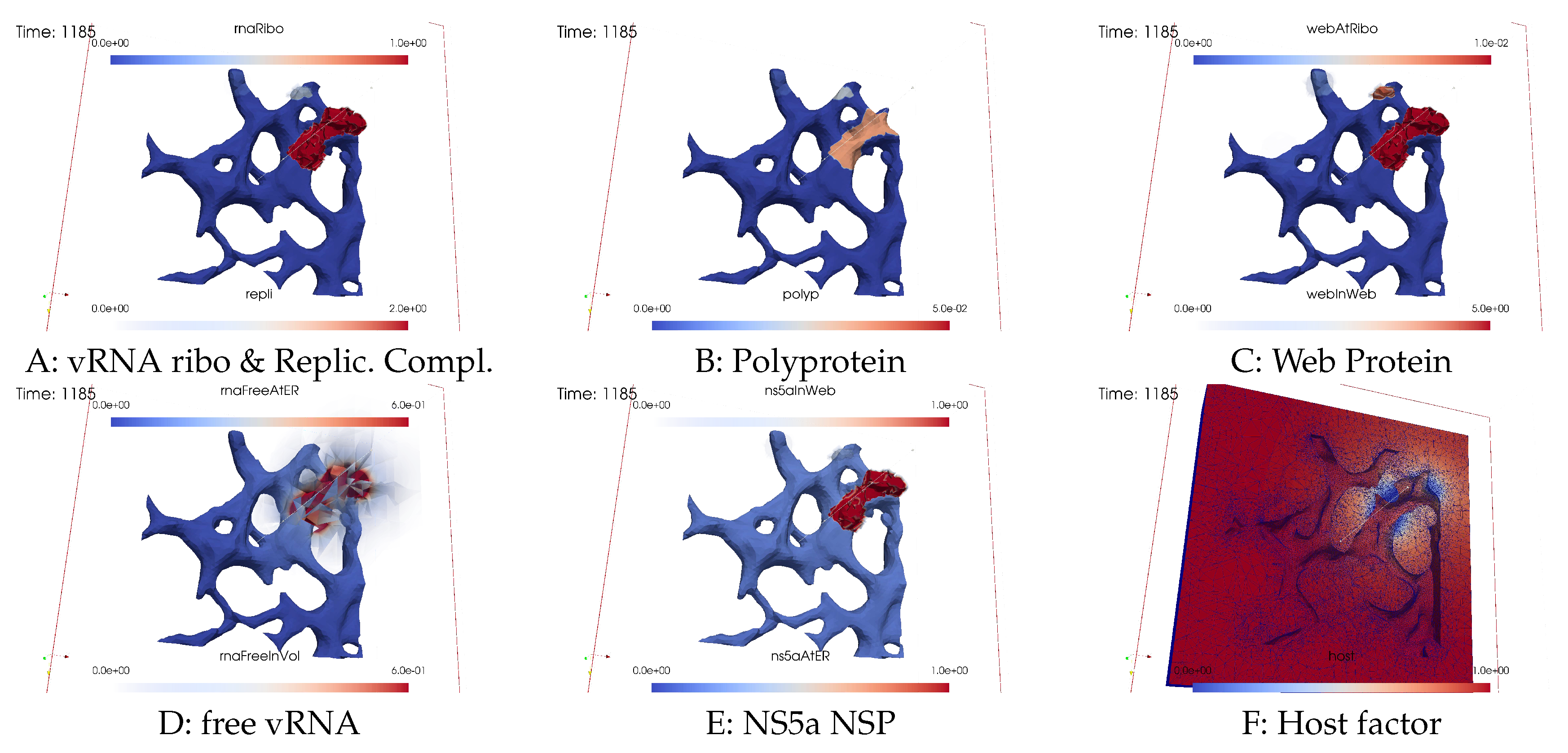
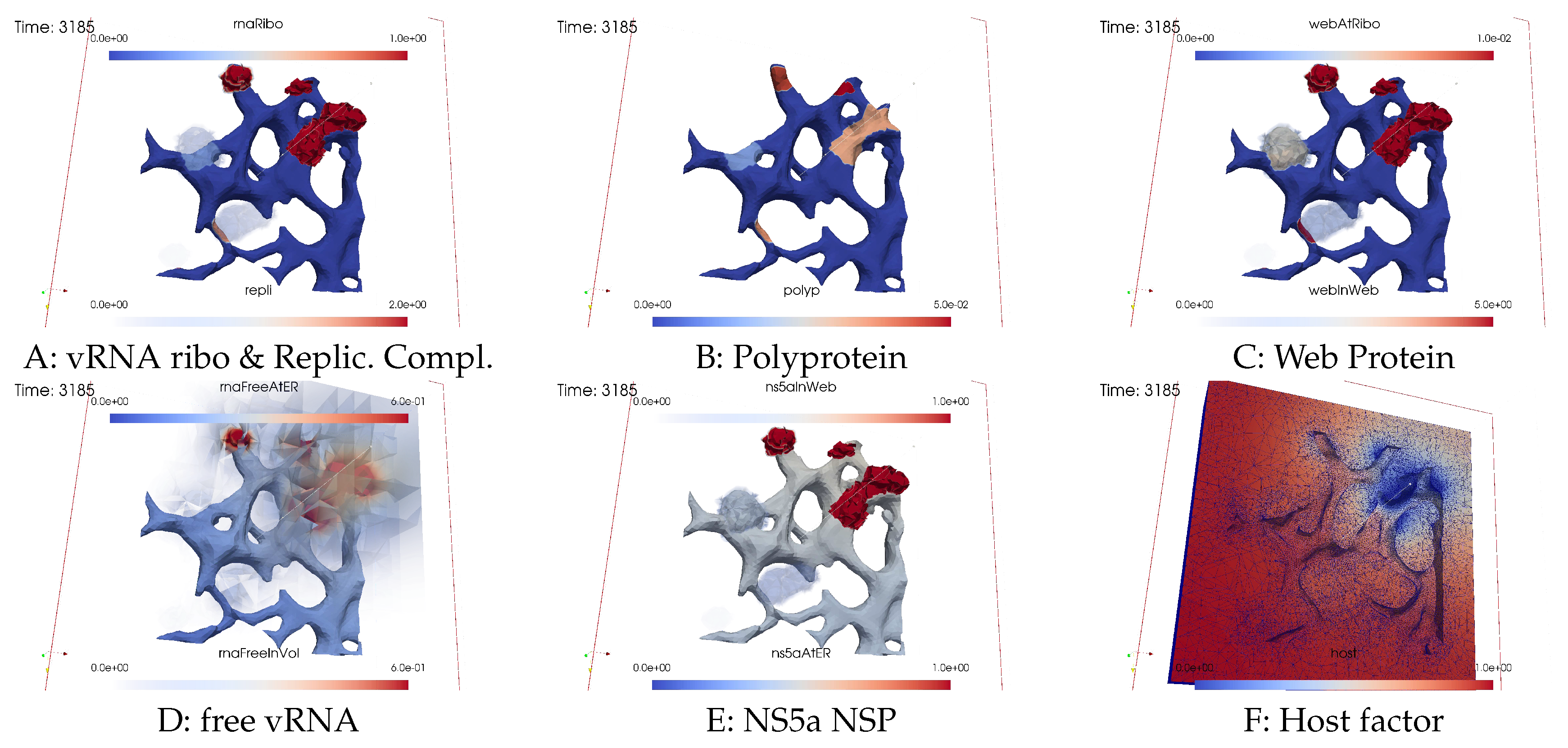
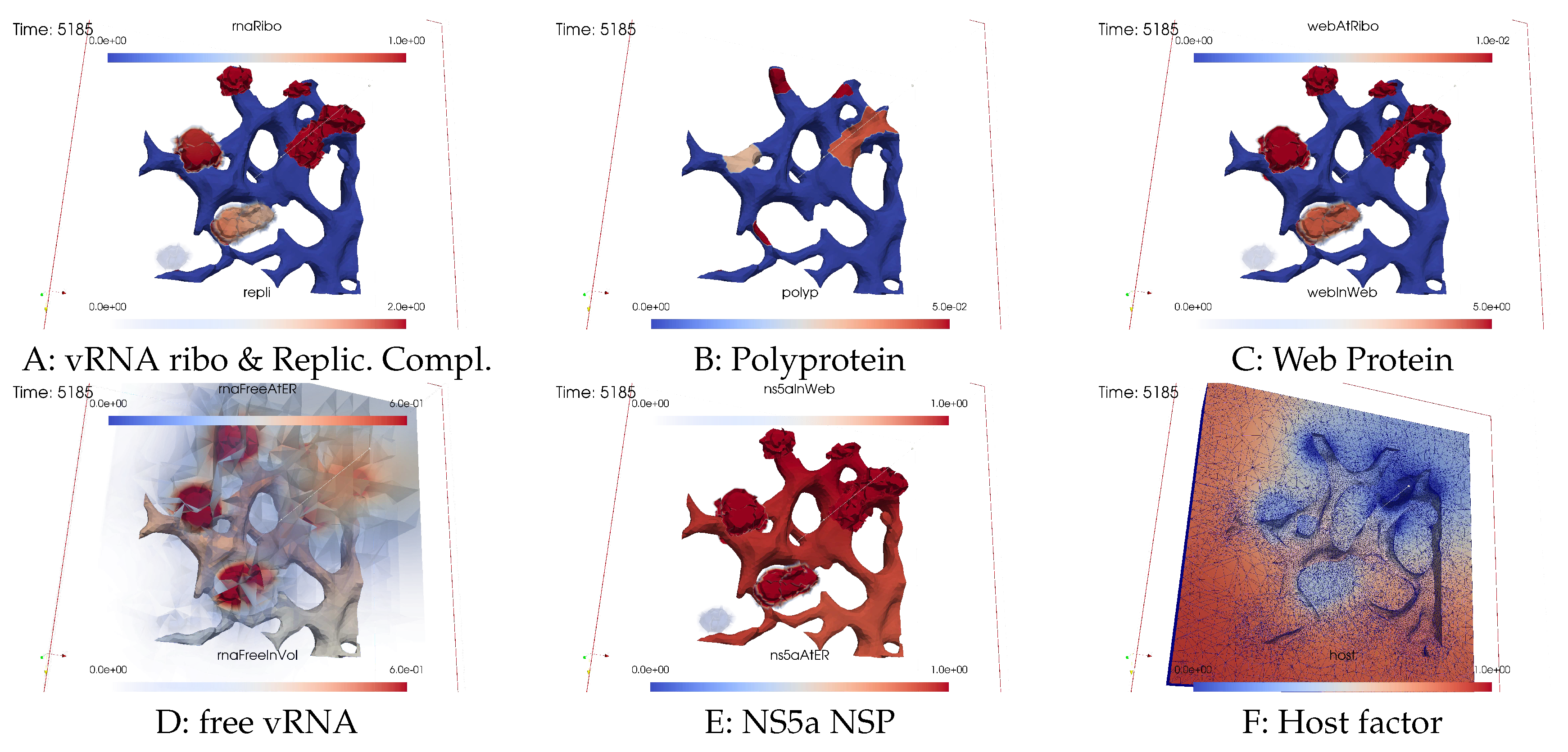
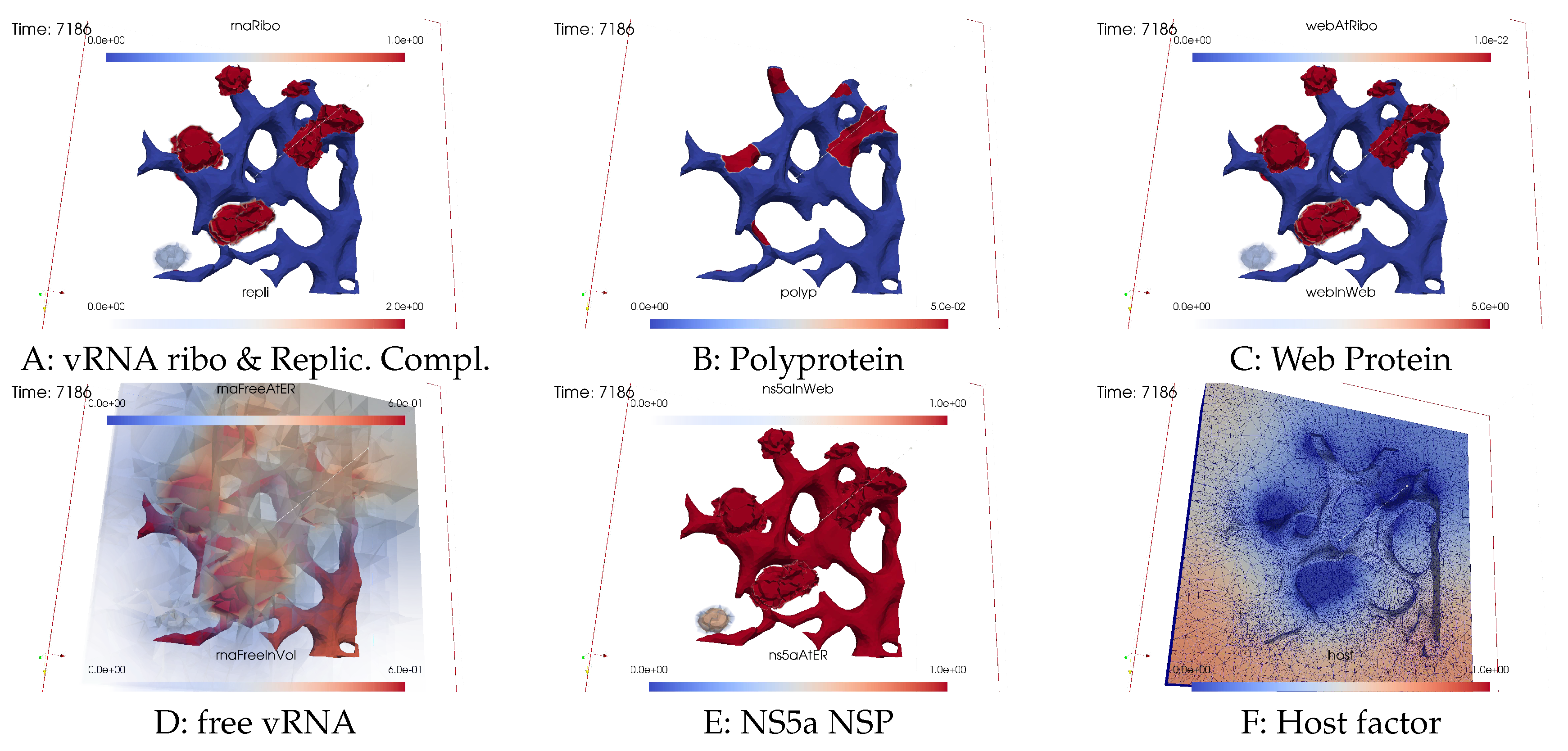
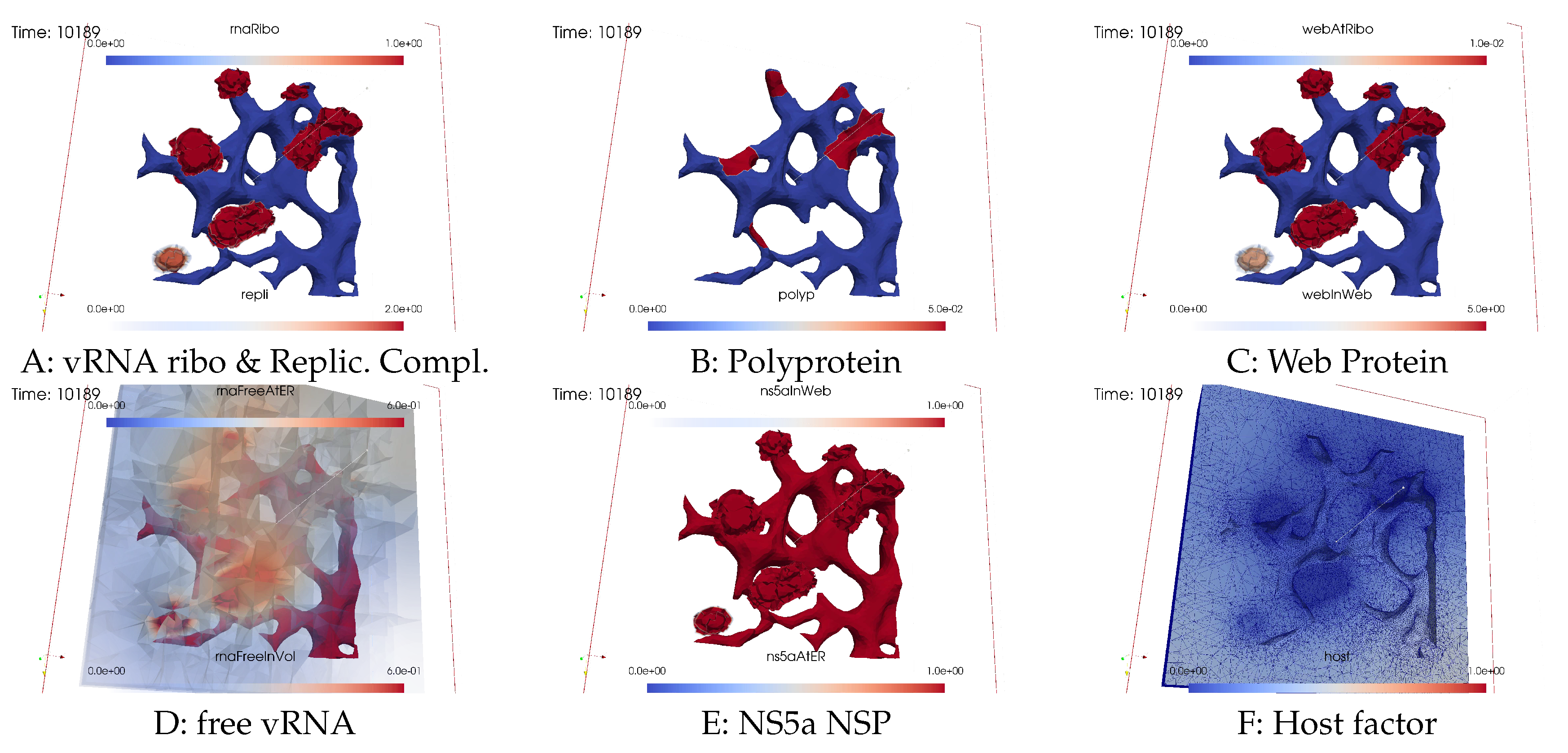
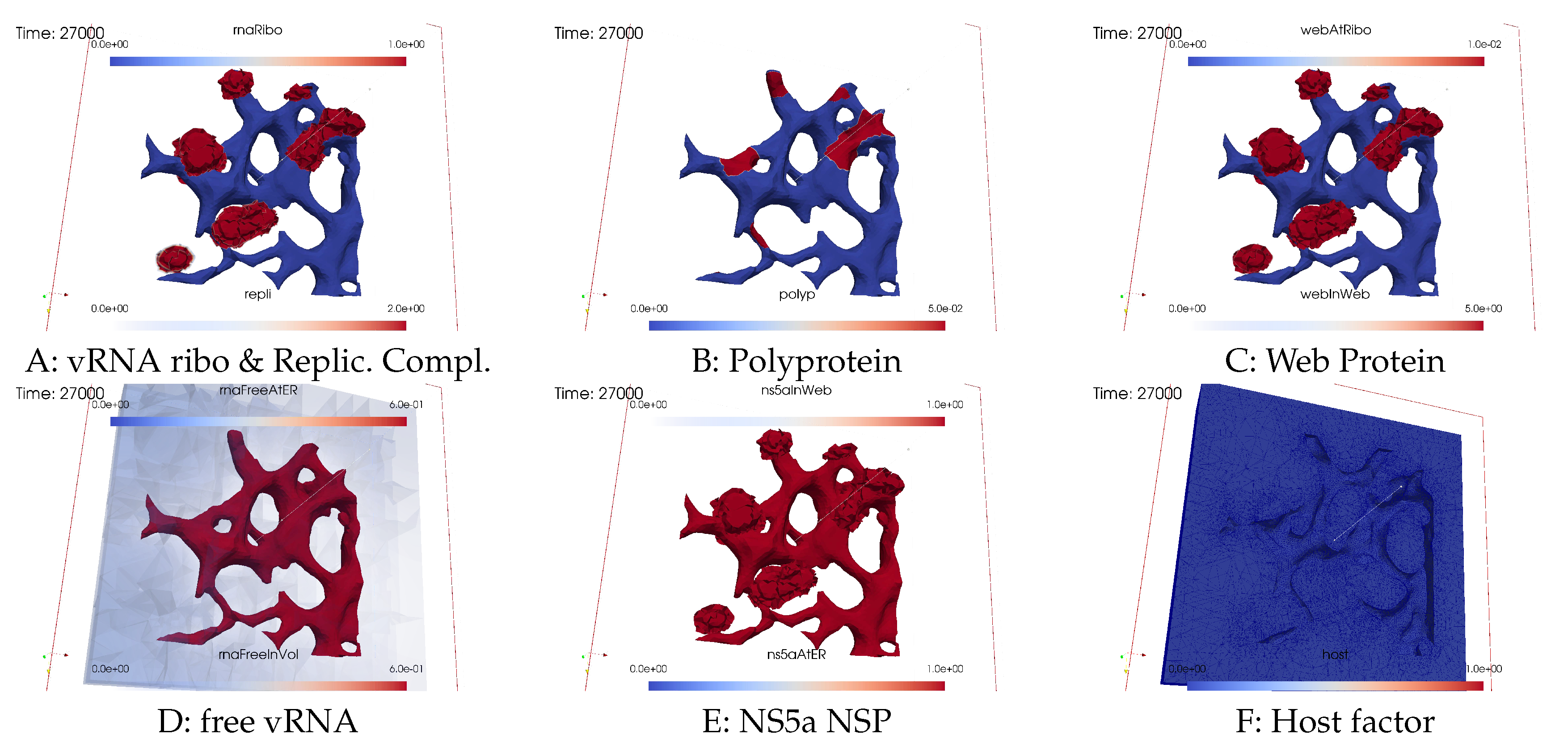
Ordering of all simulation screenshots

The subfigures show the mutually surface bound and volume concentrations of one species in the single one or in both modes as specified. The visualized panels of the different compartments are ordered identically in all time points of the spatial simulation screenshots (the letters coincide with the subindices of all simulation screenshot figures):

A

Ribosomal bound vRNA (“vRNA ribo”) on the ribosomal zones of the ER surface and RC in the MWs.

B

Polyprotein on the ribosomal zones of the ER surface.

C

WP at the ribosomal zones of the ER surface and in the MW zones.

D

Free vRNA in the volume and at the ER surface.

E

NS5a on the ribosomal zones of the ER surface and in the MWs.

F

Host factor overall in the volume.

In case of the merged perspectives, we show the ER located concentrations in all cases, but the volume concentrations are displayed with the aid of an opacity mapping based rendering procedure. This specific rendering method causes that a concentration is displayed only in case when it is above some specific threshold, else the volume is transparent. The host factor is displayed by means of a clip plane which discloses the volume grid. No opacity mapping based rendering is applied, and the volume grid elements are visible.

The simulated time is displayed in the unit of seconds.

In case of one of the two the simulation movies given in the supplemental material, we only visualize ribosomal vRNA / RC, WP, free vRNA, and host factor. Polyprotein and NS5a is omitted to enable the focus on the major effects. The other movie incorporates all components, as in the screenshots.

Initial state - one vRNA attached to one ribosomal zone

At the beginning of the simulations, the cell in considered to be “healthy” except for one vRNA which is already attached to one ribosomal region, cf. Figure 4.

Viral protein production, movement, and MW zone activation

As next step in the beginning of the simulation, the viral polyprotein is translated from the ribosomal bound vRNA and remains restricted to ribosomal zones which are part of the ER surface.

Figure 5 shows a screenshot of the in silico microscope at $t\approx 2$min:

The polyprotein cleaves into NSPs. Our model describes WP and NS5a. Other specific NSPs are not differentiated in our model so far. WP and NS5a movement remains restricted to the ER surface. Nevertheless, WP already starts to accumulate to remodel the ER surface, it detaches from the ribosomal zones and diffuses into the geometrically defined MW volume zone. Considering Figure 5 at $t\approx 2$min in more detail, we can see weakly that WC has already begun to exist in the first WM zone on top of the first ribosomal region, and thus has already activated this MW zone: The WP concentration in the volume of the MW subdomain indicates the growth of the MW zones on top of the ER surface. Therefore, the volume concentration of WP in the geometric MW zone biophysically “activates” this MW zone. WP accumulates in the volume (of the experimental data based geometric MW subdomain). This volume cluster of WP is a biophysical MW zone. The MW grows on top of the ribosomal region where the translating vRNA is attached.

The nonlinear structure of the mathematical model ensures that NS5a can detach only from the ER surface once when the MW is already biophysically active, i.e., once when the concentration of WP is nonzero inside the MW volume. Therefore, NS5a is only visible at the ER surface at this time point. As the MW zone is comparably new, NS5a is not yet visible inside. The same holds true for the construction of the RC. Therefore, at this stage, RC is nearly not visible either. If one has a very sharp view, one can detect it weakly in the volume. We can even imagine already first hints that the process of RC construction and RC appearance within this region has started even so it is still at a very low level. As we use a concentration model, we can detect also small concentrations at this early stage. The Michaelis-Menten model inspired popolation dynamics limits the biophysical action for low concentrations substantially. The concentration is still low and does not polymerize vRNA so far, as vRNA is not yet visible in the volume.

vRNA polymerization and propagation

Figure 6 shows a screenshot after about $t\approx 10$min.

As soon as the MW zone is becoming more dense, NS5a detaches in substantial amount from the ER surface and enters the MW volume as well. The observation of NS5a yields that it is also diffusing away from the first ribsomal zone on the ER surface and in part, detaching from the ribosomes and entering the MW zone.

The RC is a combination of ribosomal bound vRNA with a defined amount of ribosomal bound WP. Ribosomal bound vRNA detaches mutually with WP from the ribosomal zones on the ER surface. They combine themselves in a defined relation to form RC inside the active MW zone volume. As RC can only exist in the MWs, the MWs are the replication centers for vRNA. At this stage, the RC is visible. In the visualization, it “covers” the remaining ribosomal bound vRNA.

Once when the first active MW is filled with substantial amount of WP, NS5a and RC, it begins to polymerize new (free) vRNA which can move in the complete volume, but with enhanced “velocity” inside the MW, mathematically due to additional contributions to the diffusion coefficient inside the MWs.

We observe how the free vRNA starts to get polymerized within the first MW zone. Part of the free vRNA diffuse away in the cell volume inside the cytosol, while other parts attach to the ER surface. At this time point, the diffusion of the vRNA away from the MW zone where it was produced is already slightly visible. Free vRNA can attach to the ER surface. This process however is not visible so far on the ER surface.

In the course of the vRNA polymerization, the host factor is consumed. Its concentration starts to decrease in the region of the active MW zone. However, the effect is still moderate as additional host factor is supplied and substitutes in part the lacking host factor in the active MW zone.

Closing the vRNA cycle

Some of the newly polymerized vRNA diffuses from the MW into the cytosol. Another part attaches at the ER surface and diffuses away on the manifold. Therefore, in the cytosol and at the ER surface, substantial amounts of vRNA become visible.

Figure 7 displays a screenshot at $t\approx 20$min. It shows attached free vRNA at the ER surface, further free vRNA that diffuses away and binds to the second ribosomal zone.

Once attached to the ER surface, the vRNA can either get catched again by the local ribosomes, or diffuse away to other ribosomic zones. Our model is constructed such that the total amount of vRNA per ribosomal zone has a clear and definitive limit. Only a defined natural number, in the simulations shown here the value is one, is allowed as maximum per ribosomal zone. If more vRNA is present on the ER surface of the ribosomes, it cannot be catched any more and will diffuse away.

In our model, diffusion speed of vRNA on the ER surface is “shutled” by the NS5a concentration: The diffusion coefficient is mathematically constructed such that the presence of NS5a enhances the diffusion coefficient. However, the model parameters can be chosen also to disable the influence of NS5a upon vRNA diffusion speed. Moreover, the diffusion coefficient is nonzero also in case when NS5a is not present locally.

Governed by diffusion on the ER surface, some free vRNA arrives at the ribosomal zone neighbored to the first ribosomal zone, where the first vRNA was attached, and hence neigboured to the first active MW. This ribosomal zone catches some of the so far freely diffusion ER surface bound vRNA. The vRNA binds to the second ribosomal zone and translates new polyprotein. This polyprotein starts the same process as on the first ribosomal zone: It cleaves into WP and NS5a. In this way, the vRNA cycle is already closed.

At this stage, so far, we do not detect the second active MW zone, i.e. the WP concentration in the volume is invisible so far. However, this will follow soon.

Illumination of MW spots like a domino effect

Once the viral protein production has also started on the second ribosomal region, the cleaved WC detaches from the ribosomes and establishes the next active MW zone. RC is formed and polymerizes vRNA also inside the second MW zone already.

Figure 8 shows the next activated MW zone at $t\approx 40$min.

The host factor is already reduced in the zone of the first active MW.

Indeed, the newly synthesized vRNA which is now arising also from the second MW zone has already arrived at the next, the third, ribosomal zone. The vRNA is already attached to these ribosomes and has induced MW activation there which starts to become visible.

As the next MW zone is now active and further NSPs are produced at the active ribosomal zones, the previously observed effects are roughly repeated: WC accumulation, NS5a entry, RC construction and infiltration and, finally, vRNA polymerization which itself in part diffuses away and in part attaches to the ER surface. On the ER surface, the diffusing free vRNA arrives at the next ribosomal zone, attaches there, translates polyprotein, and so on.

Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 go along the domino effect like procedure, from $t\approx 50$min with intermediate steps until at $t=7.5$h.

We describe the replication steps shown in these figures in summary, for single events, please refer to the figure legends.

The domino like cascade causes the “illumination”, i.e. activation, of more and more MW zones followed by vRNA polymerization therein. The vRNA polymerization cannot be stopped as long as the host factor is nonzero.

The host factor gets reduced more and more, most strongly at the already active MW zones. The supply of host factor from the cytosol surrounding the MWs causes the decrease of host factor not only in the MW zones but also the cytosol itself. First locally, later globally.

Activation of new MW zones continues together with the related effects while former replication centers have to strongly reduce the vRNA polymerization because of host factor lack. Then, the vRNA polymerization nearly stops within the respective MW zones and the vRNA spots begin to disappear (due to diffusion caused blurring) following the same ordering as in the case of their appearence. The MW zones as well as the NSPs and the RC filling them remain. The resulting remodeling of the ER remains.

After about 3 hours, all MW zones are activated and have already polymerized vRNA. The majority of the MWs actively polymerize vRNA at this stage. However, at some MWs the strong vRNA spots in the volume already have blurred strongly due to a lack of host factor.

Finally, all vRNA concentration spots get blurred as the vRNA distributes in the volume, it diffuses away in the cytosol, binds to the ER surface, attaches to ribosomes, and gets bound together with WPs to form RCs.

At the end of the simulated biophysical time, most of the host factor is depleted while most of vRNA is now located at the ER and within the RCs inside the MWs.

Note that visualization is limited as we keep the same scale for each of the respective concentrations over the complete simulation time. Some concentrations seem not to increase any more once when they show red color. However, this is not necessarily the case. Concentrations can still increase above the highest color value shown in the scale. Similarily, small values near zero are difficult to visualize.

We recall that one of the two supplemental movies attached to this study shows the simulation progress of the “in silico microscope” in a compact way displaying the major components for a better overview, while the other displays all components (as here).

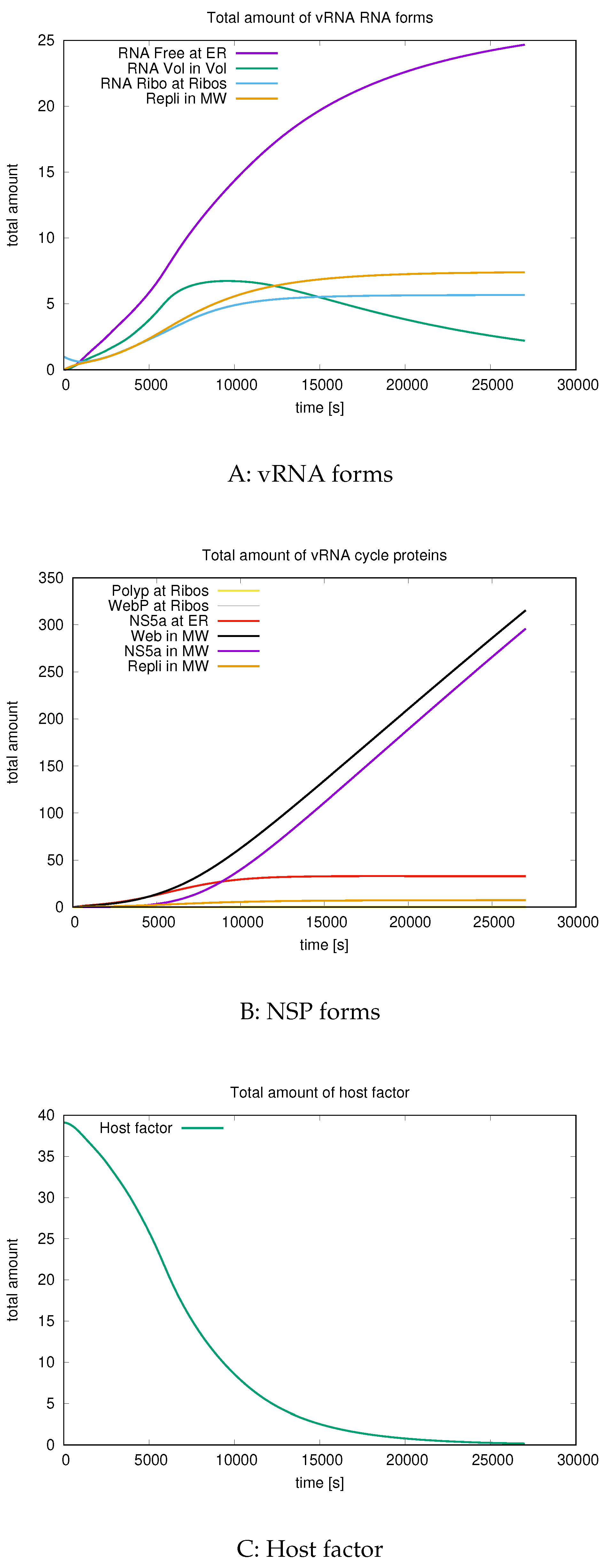
3.3. Quantitative data evaluations

To compute the total number of the compartments of the model, we integrate the respective concentrations as described in Section 2.6 and the equations given therein for manifold components (24) respectively for volume components (25).

The integrated concentrations of the long-term simulations aiming about 7.5 biophysical hours allow a comparison to experimentally derived values as the overall number of arising viral particles and components, namely NSPs and vRNA number, cf. Figure 15.

While the entire biophysical results of this study are exclusively presented in this study, in [56], we study the numerical grid convergence behaviour of the sum of all NSPs. The sum of all forms of WP and its combinations necessarily must have the same integrated value as the sum of all forms of NS5a. This property enables an important check for the consistence of the highly nonlinear computations. The numerical methods focusing proceedings [56] demonstrates that indeed, the sum of all WP containing components equals the sum of all NS5a containing components. However, it demonstrates as well that for high consistence, high grid refinement levels should be used. Therefore, the values presented in this paper are computed at grid level 4. This allows for fully trusting the generated numerical values [56].

Our computational domain is about $10-40\mu m^3$ volume. At the end of the about 7.5 biophysical hours of simulation time, the total amount of vRNA is about 40 vRNA, and 350 NSPs in this domain.

If we assume a typical hepatoma cell to cover a volume of about ${10}^2-{10}^3\mu m^3$ [32,33,34,39], the volume of the computational domain covers about 1-10 % of such a typical cell.

Multiplying the computational domain numbers with the volume upscale factor, we would have about 400-4000 vRNA and 3500-35000 NSPs.

If we upscale the amount of produced viral components to the size of a complete cell, the values are compatible with experimental data and ODE model data [21].

For a detailed discussion and comparison, we refer to the discussion Section 4.6.

3.4. Mass conservation along exchange between manifold and volume

We performed extensive investigations to ensure that the mass of components is conserved when they interchange between manifold and volume.

A detailed demonstration is shown in [41].

Of course, the overall total masses of single concentrations cannot be conserved in the course of virus replication, as else, the cell would stay healthy, and no virus components could be produced. However, this is not meant when we speak about mass conservation.

4. Discussion

We have presented fully 3D spatially resolved simulations of the HCV RNA cycle.

The simulations were performed at a cutout part of a realistic reconstructed hepatoma cell based on fluorescence z-stack data of hepatoma cells [36]. The model combined processes restricted to the 3D embedded 2D ER surface manifold with others taking place in the full volume of cytosol and MW regions. The model is based on former spatial modeling of us [32,33] which was restricted to surface effects exclusively and incorporated only qualitative effects. Independently, we had started to estimate spatial parameters of such models [34] based on experimental FRAP time series for spatial NS5a dynamics [57].

The model simulations presented in this paper unify the former sockets and augment them with the full incorporation of volume effects. We investigated the biophysical as well as the numerical properties [41] of the model and the solvers to ensure the well-foundation of the simulated values.

Our model aims to simulate the major steps of the interaction between the major compartments of the HCV RNA replication cycle in a fully spatio-temporal resolved manner. The quantitative evaluation of the results are consistent with published experimental data. However, as spatially resolved data were not accessible for us so far, we could not yet validate the spatial part of the model with experimental data.

In the following, we discuss several properties of the results which we have observed and which may be used for model validation and further model improvement,

4.1. Model components and their respective spatial dynamics

The model incorporated the major compartments of the vRNA replication cycle, namely vRNA, two forms of NSPs, and a generic host factor. Modelling of their spatial properties has two aspects: Location patterns and movement dynamics.

While some of the components exist only at the ER surface and others only in the volume, some components can be present in two modes as they can move on the ER surface as well as in the MW / cytosol volume.

The NSPs are modeled as residing exclusively on the ER surface and the generic host factor is modeled as to be in the full volume without any kind of explicit surface restricted mode.

The new model nevertheless enables the NSPs to accumulate to form MW zones, for details cf. Section 4.2.

For the vRNA, modes at the ER surface and modes in the volume are possible, cf. Section 4.3.

All compartments are assumed to underlie passive transport only. Therefore, the model basis is of diffusion-reaction type. However, the diffusion and reactions coefficients are selected such that they allow for realistic process modeling, cf. 4.5.

4.2. ER surface remodelling / MW zones establishment

Our model takes into account that each kind of NSPs (WP and NS5a) attaches to the ER surface directly after their cleavage and their movement is restricted to the ER surface. However, the NSPs cause the remodelling of the ER surface by means of clustering together to form MW zones. This remodelling is reflected by the growth of the MW zones.

Our model simulations describes the growth of biophysically active MW zones in the following way: At the beginning of the simulation, the full volume surrounding the ER surface is considered to act as functional cytosol. WP once cleaved can detach from the ER surface and move into the potential MW volume subdomain. The potential MW subdomain is part of the volume and clearly defined by the experimental z-stack data [36], see also Section 2.7 for more details of this modelling approach.

We consider the arising WP concentration inside the MW volume zone as “activation” of the MW zone. In the context of our framework, NSPs cause ER remodelling by WP detachment from the ER and diffusion into the respective potential MW zone. Note that we restrict WP diffusion to the experimentally defined potential MW zones.

4.3. vRNA movement and location

Experimentally, the spatio-temporal dynamics of HCV RNA is not described so far [35]. Mathematical model approaches allow to mimick different hypothesis and to predict typical scenarios following them.

In this context, we focus on two major properties: vRNA location and vRNA transport properties.

Concerning the location, it is interesting to clarify experimentally wether vRNA attaches to the ER surface, similar to the NSPs, or whether it moves only in the cytosol volume or wether both modes are possible. Our model to date incorporates both modes, but can easily be restricted to one specific mode if experimental knowledge requests so.

Concerning the transport mechanisms, in principle, passive and active transport are possible. Typically, modeling starts with passive transport diffusion models and we also follow this approach. For future work, active transport can be added if there is experimental evidence.

Evaluating the presented simulations teaches us:

If vRNA transport is based on diffusion, the transport mode along the ER surface is much more efficient as the transport move in the cytosol volume. The diffusion in the volume leads to such a blurring of the volume vRNA concentration that only few vRNA really arrives at other ribosomal regions. Hence, this form of transport seems to be not efficient in contrast to passive transport along the ER.

To enable efficient volume transport, it is tempting to envisage the incorporation of active transport terms in the model, i.e., to incorporate advection terms in future studies and to analyze if such terms enable descriptions closer to future spatial experimental data. Nevertheless, as long as such data is still missing, we did not incorporate advection active transport terms for the vRNA into the PDE model.

As vRNA volume diffusion is not efficient in our model, our model requests that vRNA which is polymerized in the MW volumes cannot directly attach to ribosomes. Moreover, vRNA newly polymerized in the MWs diffuses in the MWs and in the cytosol, but can attach to the ER surface. Once attached to the ER surface, free vRNA diffusion is comparably efficient. Free vRNA can diffuse to other ribosomal regions located at the ER surface and can be bound as ribosomal vRNA.

Note that in our model, the total number of possible vRNA at a ribosomal region is restricted to a natural number which we can select. In our example, we restricted this number to one.

As we assume that the cut set of reconstructed ER surface and reconstructed MW boundaries indicate ribosomal regions, and as we assume that the MW regions grow on top of such ribosomal regions, the restriction that a maximum amount of vRNA can be bound per ribosomal region indicates that different sized ribsomal surfaces need to be able to capture different concentrations of vRNA. Our model realizes this by means of specific prefactors of the reaction term which allows the capturing of ER surface attached free vRNA to a ribosomal region, cf. (3) and (7).

In addition, our model incorporates the possibility that the vRNA diffusion is “shuttled” by NS5a in the sense that NS5a facilitates vRNA transport. This property is optional and can be switched off by setting $k_1=0$ and $k_3=0$.

As we have introduced the NS5a “boosted” vRNA transport already for our qualitative surface model [33], we refer to this paper for more detailed considerations in this context.

4.4. Replication complex and cis condition

The replication complex is modeled as a combination of WP and formerly ribosomal bound vRNA.

This is reflected in the reaction coefficients of $W_C^S$ and $R_R^S$ of the sufPDE system (3)-(7) on the side of detachment of the components. On the side of the PDE system for $C_W^V$, this is reflected by the boundary conditions (13) for $C_W^V$.

We have already introduced this concept of combination in our previous study [33]. As all processes were restricted to the ER surface in the previous model, it was possible to realize also the combination of RC in the formula of the analogon of $C_W^V$ as reaction term. Due to the coupling of volume and surface effects, here, the concept is implemented by the boundary conditions (13) of the PDE system (8)-(12).

As already described in the former paper [33], the interaction of vRNA with WP in forming RC realizes the so-called “cis-requirement” [37,38,58] in the mathematical model. The cis-condition indicates in brief that an vRNA can only be replicated by the NSPs which origin exactly in this vRNA. Moreover, this is not an input of our approach but a result.

Similarly the spatial model sense of this study describes that WP as cleaved part of the polyprotein is translated by the vRNA bound at some ribosomal region that cannot move to any MW zone except for the MW zone which belongs to this ribosomal region. As the RC is a combination of WP produced at this ribosomal region with vRNA which translated exactly this WP, each RC can again only reproduce the vRNA from which it was derived.

For more biology-oriented details of the cis condition and the mathematical realization, we refer to the former study [33] as the principles can be easily translated to the present model.

We stress that our model framework is, to the best of our knowledge, the only existing mathematical model of virus replication which mimics the cis-requirement.

4.5. Nonlinear diffusion and reaction coefficient structure

The nonlinear form of diffusion and reaction coefficients of the general form

$$\frac{Q}{Q+p}$$

(26)

of a concentration unknown Q with a constant coefficient p enables to replace linear term structures that are unbound and are realistic only for small concentrations [33].

This structure was already proposed in [33] and allows for comparably sharp transitions between the switching-off of a function for small concentrations and switching it on for relevant concentrations. Moreover, it allows for a plateau value, a maximum value, for huge concentrations.

The implementation of such terms instead of a constant value for the diffusion coefficients of $W_R^S.W_W^V$ and H allows to facilitate modelling of the movement of WP and host factor inside the MW zones when the WP concentration is sufficiently high. Moreover, the diffusion coefficients of $N_W^V,C_W^V$ enable to model that NS5a and RC can enter the MWs only in case when WP concentration is already present. Without WP in the MW subdomains, neither NS5a nor RC can enter. This accounts for the fact that NS5a and RC cannot enter a so-far non existing / active MW zone.

For more explanations concerning nonlinear structured diffusion and reaction coefficients, we refer to [33].

4.6. Comparison to quantitative experimental data

Based on experimental data, Dahari et.al. [21] report the total amount of viral RNA and NS5B of a typical hepatoma cell after about 2 days of infection to be in the size of magnitude of about ${10}^3-{10}^4$ for plus stranded vRNA and about ${10}^6$ for NS5B. As all NSPs occur at the same amount if we neglect decay processes, we can transfer this size of magnitude number to each NSP.

Comparing these data to our simulation results which we computed for a about 1% to 10% of a cell and for a time scale of about half a day, our simulation data are overall in accordance with these experimental studies.

4.7. Quantitative model validation

Unfortunately, validation of the spatial patterns of our simulation is not yet possibly. For future adaption and validation of our model, such spatially resolved experimental data will be indispensable.

Overall we feel that our model is a reasonable compromise between including the most important details and overparametrization by including more details as can be validated. This may be true even if a considerable amount of parameters and complexity is still included.

An example for non-living world scenarios is the Standard Model of Electroweak Interactions (SM) which describes the fundamental properties of the elementary particles of this world [59,60]. Without the use of a highly complex model with a very huge number of parameters, the understanding of major basic mechanisms in the non-living world would not have been possible. In fact, this extremely complex model enabled the detection of the Higgs boson [61] which was, for years, the last missing buildstone of the SM. It was predicted by the SM for many years but not validated experimentally until some years ago.

As the living world is even more complex, a considerable number of parameters may be needed in realistic biophysial models.

4.8. Relation form and function

Spatial models may be helpful is to understand the relation of form and function.

Already in the first model publication in this context, [32], we performed a spatial investigation. Even a simplified spatial model allowed to reconsider and reinterpret the relation of host diffusion coefficient, host initial value, and overall vRNA synthesis rate.

In this study, we concluded from parameter sensitivity studies that vRNA diffusion in the volume is quite ineffective in comparison to vRNA diffusion at the ER surface (data not shown) independent of the vRNA diffusion coefficient in the volume. Hence, this study supports, among others, that it seems to be unlikely that passive vRNA transport in the volume might be the major source of vRNA movement in the cell.

Of course, this statement holds true only as long as the vRNA transport properties are governed by diffusion and are purely passive. If advective active transport terms would contribute, this results would change substantially. Such investigations will be interesting for future studies in combination with experimental studies.

4.9. Qualitative model properties

The qualitative model properties of the model structure, in principle, do not differ from those described already in the former study [33]. We had claimed in this paper that the incorporation of volume effects would not change the qualitative properties, but only the quantitative ones, and this still holds true.

Therefore, we refer to [33] for an extended overview over the model structure beyond the explainations presented here as well as for possible model extensions concerning the general model structure.

4.9.1. Summary - in silico microscope

In fact, the visualization of the computer simulations which we performed on the HLRS Stuttgart Apollo Hawk supercomputer now really resembles the look into some sort of “in silico microscope”.

In this paper, we have shown how our new model recapitulates major experimental issues of the vRNA replication cycle not only in qualitative way but also in a quantitative way.

Indeed, our fully spatio-temporal resolved simulations resemble experimental major facts of the vRNA cycle and hence reproduce experimental results in such a way that watching the simulation movies showing the spatially resolved dynamics of the major components of the vRNA cycle give some insight in what may be observed looking through a microscope into a real in vitro cell.

Moreover, the integrated values of the components over the computational domain serve as indicator for comparisons with existing data and ODE model values.

The quantitative values of the temporal development of the vRNA and NSPs of the present study indeed are in a range which is biologically very plausible and are comparable to the values given in the literature based on experimental data as well as given by ODE model kinetic data [21].

Despite the fact that our virus model simulation framework thus has reached an important mile stone, the model still needs to pass important validation tests.

In silico methods developed for HCV may be transferred to other vRNA viruses, e.g., to the quite similar family of Coronaviridia such as the SarsCov2 virus.

Fundamental understanding of virus replication mechanisms at a cellular level might help to unveil the mechanisms viruses apply in order to replicate themselves at the most basic level. In consequence, profound basic understanding of virus mechanisms might help to develop efficient direct antiviral agents (DAAs) which allow to stop virus replication at its entire root, which is the single human and animal cell, wherein the virus replicates itself. Furthermore, detailed understanding of virus replication mechanisms might help understand to develop efficient and long lasting vaccines, as they exist already for example for the Yellow fever virus [62] which however was not the result of systematic research, but more the result of a lucky experiment about 80 years ago which even could not be repeated afterwards.

In the long run, our framework might help to facilitate the development of efficient but economic DAAs, and long-lasting sterile vaccines with only few side effects.

5. Conclusions

We have simulated the HCV RNA replication cycle in a fully spatio-temporal resolved manner combining effects restricted to the ER surface manifold with those taking place in the full volume. Special emphasis was put on the exchange of components between the manifold and the volume. The simulations were performed at realistic reconstructed geometries based on experimental fluorescence hepatoma cell data.

While the overall number of vRNA and NSPs in the hepatoma cell are consistent with experimental data, validation requests for further steps. Model validation requires in particular comparison to spatially resolved experimental data.

Despite these restrictions, our results deploy the first spatial model which delivers plausible values for the number of components inside single hepatoma cells.

Our numerical simulation framework of mathematical PDE models allows to visualize and evaluate simulation data such that one can compare the evaluation techniques as some sort of “in silico microscope”. This in silico approach is complementary to in vitro / in vivo research.

The framework is not restricted to HCV but may be extended to other plus stranded RNA viruses such as SarsCov2 or Yellow and Dengue fever. With some extended adaptions, applications may also allow modelling replication cylces of other virus types. Such a framework may improve substantially the systematic biophysical understanding of intracellular virus replication mechanisms.

Our framework might also help to facilitate the systematic planning of intracellular virus research experiments looking for possible attack points for virus elimination.

In the long run, a combined complementary in vitro / in vivo – in silico approach might facilitate the design of cheap but efficient DAAs, and the development of only few side-effect containing, efficient - i.e. sterilizing-immunity inducing and long lasting - vaccines.