Submitted:
02 October 2023
Posted:
04 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. General
1.2. Terminology and Definitions
2. Embeddings of finite graphs
3. Embeddings of periodic graphs
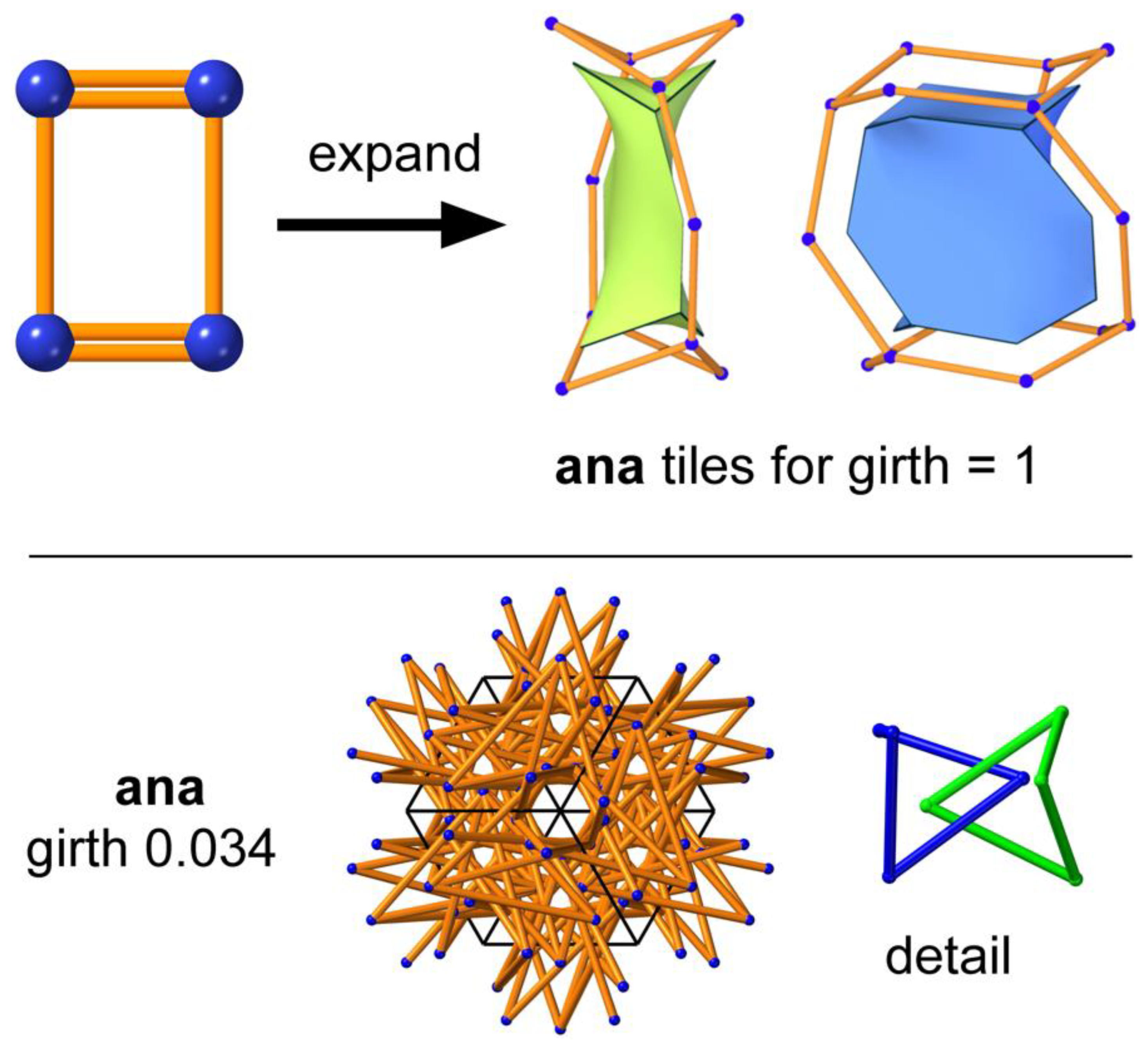
3.1. ana and rhr
3.2. bmn
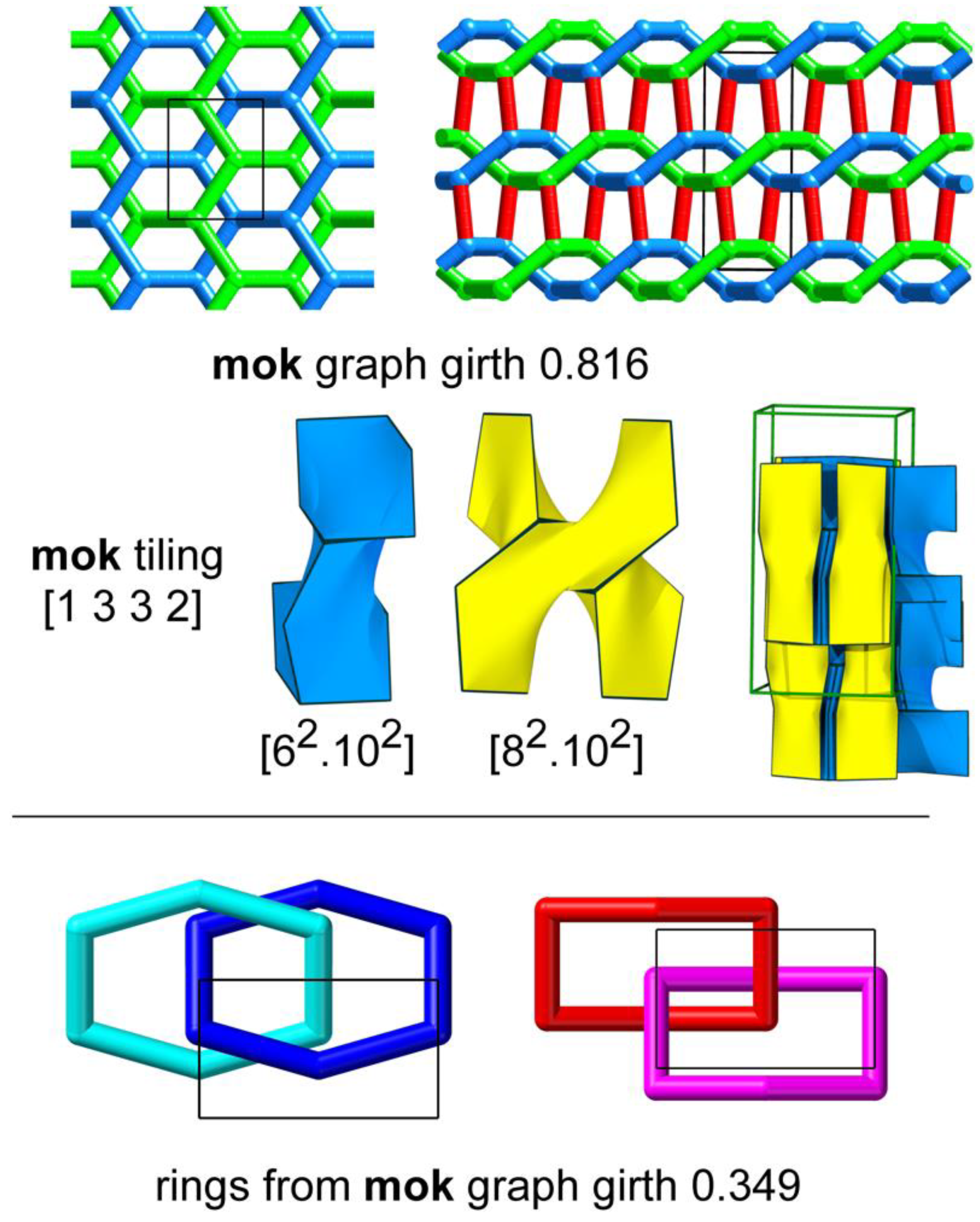
3.3. mok
3.4. jcy
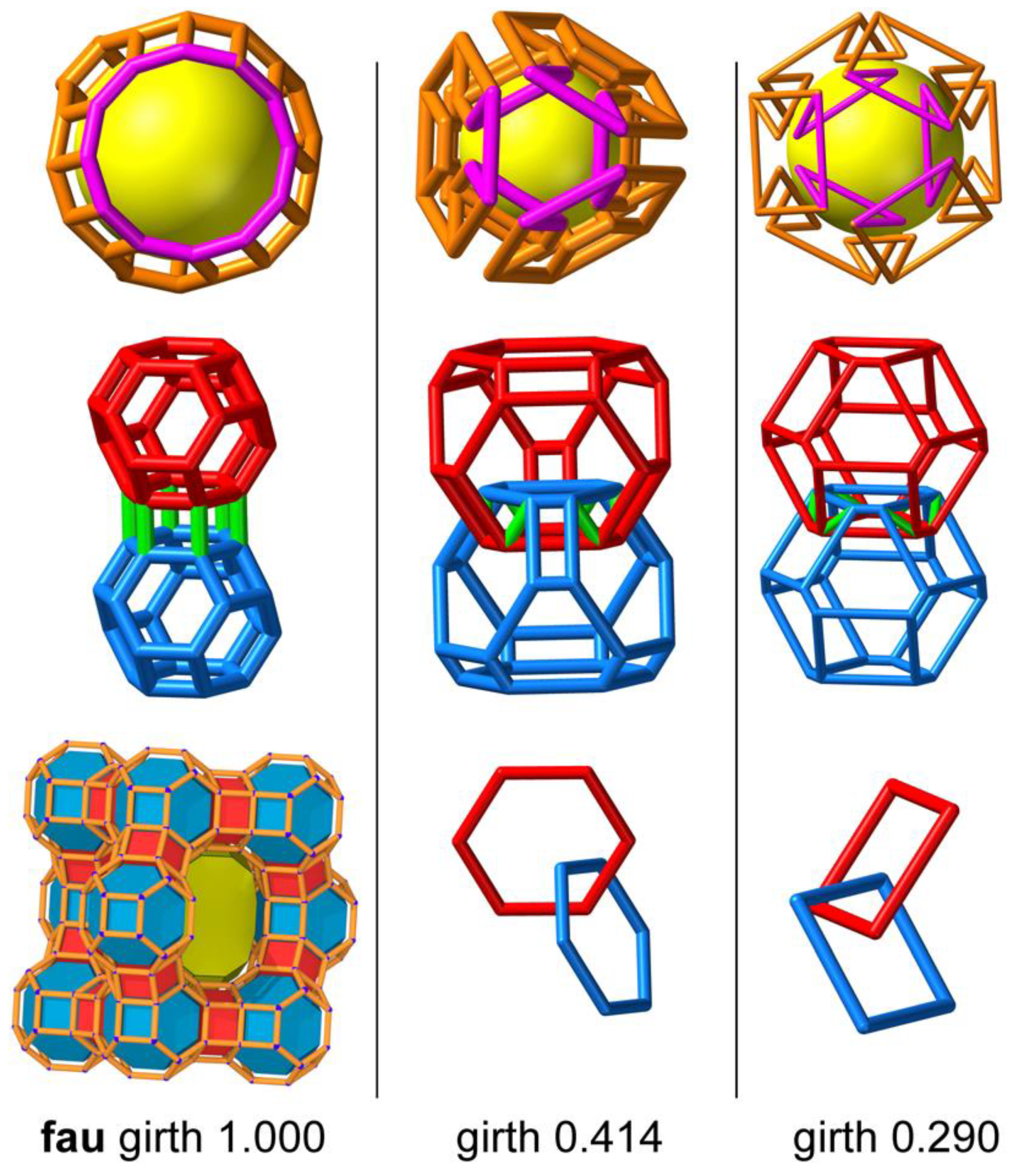
3.5. fau
4. Conclusions
References
- O'Keeffe, M. and M.M.J. Treacy, The Symmetry and Topology of Finite and Periodic Graphs and Their Embeddings in Three-Dimensional Euclidean Space. Symmetry, 2022. 14: p. 822–841. [CrossRef]
- Earl, R. and J. Nicholson, The Concise Oxford Dictionary of Mathematics. 2021: Oxford University Press.
- Blatov, V.A., A.P. Shevchenko, and D.M. Proserpio, Applied Topological Analysis of Crystal Structures with the Program Package ToposPro. Cryst. Growth Des., 2014. 14(7): p. 3576–3586. [CrossRef]
- Delgado-Friedrichs, O. and M. O'Keeffe, Identification of and symmetry computation for crystal nets. Acta Crystallogr., 2003. A59: p. 351–360. [CrossRef]
- O’Keeffe, M., M.A. Peskov, S.J. Ramsden, and O.M. Yaghi, The Reticular Chemistry Structure Resource (RCSR) database of, and symbols for, crystal nets. Acc. Chem. Res., 2008. 41: p. 1782–1789. [CrossRef]
- Blatov, V.A., O. Delgado-Friedrichs, M. O'Keeffe, and D.M. Proserpio, Three-periodic nets and tilings: natural tilings for nets. Acta Crystallogr., 2007. A63(5): p. 418–425. [CrossRef]
- Conway, J.H. and C.M. Gordon, Knots and links in spatial graphs. J. Graph Theory, 1983. 7(4): p. 445–453. [CrossRef]
- O'Keeffe, M. and M.M.J. Treacy, Tangled piecewise-linear embeddings of trivalent graphs. Acta Crystallogr., 2022. A78: p. 128–138. [CrossRef]
- 9. Möbius Ladders and Related Molecular Graphs, in When Topology Meets Chemistry: A Topological Look at Molecular Chirality, E. Flapan, Editor. 2000, Cambridge University Press: Cambridge. p. 69–109.
- O'Keeffe, M., Dense and rare four-connected nets. Z. fur Krist. – Cryst. Mater., 1991. 196(1–4): p. 21–38. [CrossRef]
- Bonneau, C. and M. O'Keeffe, Intermetallic Crystal Structures as Foams. Beyond Frank–Kasper. Inorg. Chem., 2015. 54: p. 808–814. [CrossRef]
- Baerlocher, C., L.B. McCusker, and D.H. Olson, Atlas of Zeolite Framework Types. 6 ed. 2007 (http://www.iza-structure.org): Elsevier Science. [CrossRef]
- Hyde, S.T. and G.E. Schröder-Turk, Tangled (up in) cubes. Acta Crystallogr., 2007. A63: p. 186–197.
- Alexandrov, E.V., A.P. Shevchenko, and V.A. Blatov, Topological databases: why do we need them for design of coordination polymers? Crystal Growth & Design, 2019. 19(5): p. 2604–2614.
- O'Keeffe, M., On the arrangements of ions in crystals. Acta Crystallogr., 1977. A33(6): p. 924–927. [CrossRef]
- Johnson, S., Johnson’s Dictionary Online https://johnsonsdictionaryonline.com. 2023.
- Yaghi, O.M., et al., Reticular synthesis and the design of new materials. Nature, 2003. 423: p. 705–714. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




